X 2 7 X 5
thesills
Sep 13, 2025 · 6 min read
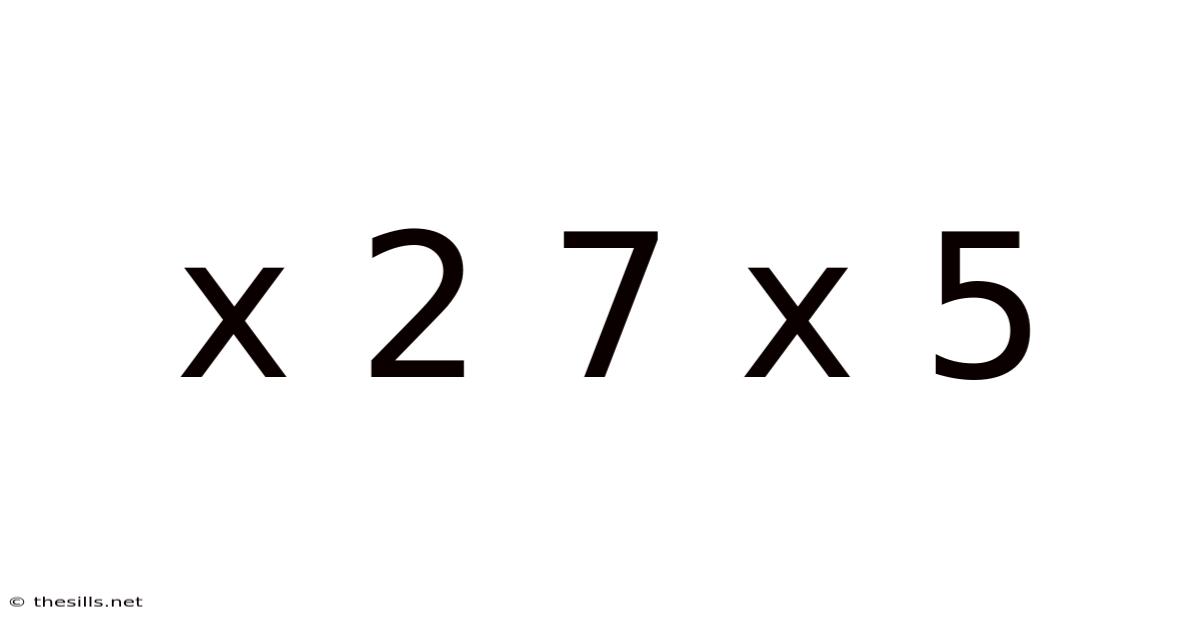
Table of Contents
Unlocking the Mystery: Exploring the Mathematical Puzzle of x² + 7x + 5
This article delves into the fascinating world of quadratic equations, focusing specifically on the expression x² + 7x + 5. We'll explore various methods to solve for x, understand the underlying mathematical principles, and examine the practical applications of such equations. This seemingly simple expression opens doors to a deeper understanding of algebra and its real-world implications. We will cover solving using factoring, the quadratic formula, and completing the square, and explore the graphical representation of this quadratic function.
Understanding Quadratic Equations
Before diving into the specifics of x² + 7x + 5, let's establish a foundational understanding of quadratic equations. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (in this case, x) is 2. The general form is expressed as ax² + bx + c = 0, where a, b, and c are constants, and a is not equal to zero (otherwise, it wouldn't be a quadratic equation).
Our expression, x² + 7x + 5, is a quadratic expression, not yet an equation. To solve for x, we need to set it equal to zero: x² + 7x + 5 = 0. This transforms our expression into a solvable quadratic equation. Solving this equation means finding the values of x that make the equation true.
Method 1: Factoring the Quadratic Equation
Factoring is a powerful method for solving quadratic equations, but it's not always possible. It involves expressing the quadratic expression as a product of two simpler expressions. Unfortunately, our equation, x² + 7x + 5 = 0, cannot be easily factored using integers. We can attempt to find two numbers that add up to 7 (the coefficient of x) and multiply to 5 (the constant term). However, no such integer pair exists. This means we need to resort to other methods.
Method 2: Completing the Square
Completing the square is a technique that transforms the quadratic equation into a perfect square trinomial, making it easier to solve. The steps involved are as follows:
-
Move the constant term to the right side of the equation: x² + 7x = -5
-
Take half of the coefficient of x (which is 7), square it ((7/2)² = 49/4), and add it to both sides of the equation: x² + 7x + 49/4 = -5 + 49/4
-
Simplify the right side: x² + 7x + 49/4 = 29/4
-
Factor the left side as a perfect square: (x + 7/2)² = 29/4
-
Take the square root of both sides: x + 7/2 = ±√(29/4)
-
Solve for x: x = -7/2 ± √29/2
Therefore, the solutions are x = (-7 + √29) / 2 and x = (-7 - √29) / 2. These are the exact solutions. Approximate values can be obtained using a calculator.
Method 3: The Quadratic Formula
The quadratic formula is a universal method for solving quadratic equations, regardless of whether they are factorable. It provides a direct solution for x given the coefficients a, b, and c in the general quadratic equation ax² + bx + c = 0. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our equation, x² + 7x + 5 = 0, we have a = 1, b = 7, and c = 5. Substituting these values into the quadratic formula gives:
x = [-7 ± √(7² - 4 * 1 * 5)] / (2 * 1) x = [-7 ± √(49 - 20)] / 2 x = [-7 ± √29] / 2
This confirms the same solutions we obtained using completing the square. The quadratic formula is a powerful tool because it always works, even when factoring is not feasible.
The Discriminant: Understanding the Nature of Roots
The expression inside the square root in the quadratic formula, b² - 4ac, is called the discriminant. It reveals valuable information about the nature of the roots (solutions) of the quadratic equation:
-
If b² - 4ac > 0: The equation has two distinct real roots. This is the case with our equation, x² + 7x + 5 = 0, since 49 - 20 = 29 > 0.
-
If b² - 4ac = 0: The equation has one real root (a repeated root).
-
If b² - 4ac < 0: The equation has two complex roots (involving imaginary numbers).
Graphical Representation of the Quadratic Function
The quadratic expression x² + 7x + 5 represents a parabola when graphed on a coordinate plane. The roots of the equation x² + 7x + 5 = 0 represent the x-intercepts of this parabola – the points where the parabola intersects the x-axis. Since we found two distinct real roots, the parabola intersects the x-axis at two distinct points. The parabola opens upwards because the coefficient of x² (which is 1) is positive. The vertex of the parabola (the lowest point) can be found using the formula x = -b/2a, which in our case is x = -7/2. Substituting this value back into the original expression gives the y-coordinate of the vertex.
The graph visually confirms that the parabola intersects the x-axis at two points, corresponding to the two real roots we calculated.
Applications of Quadratic Equations
Quadratic equations have numerous applications in various fields:
-
Physics: Calculating projectile motion, determining the trajectory of objects under the influence of gravity.
-
Engineering: Designing structures, analyzing stress and strain on materials.
-
Economics: Modeling supply and demand, optimizing production costs.
-
Computer graphics: Creating curved shapes and animations.
Frequently Asked Questions (FAQ)
Q1: Why is factoring not always possible for solving quadratic equations?
A1: Factoring relies on finding integer pairs that satisfy specific conditions related to the coefficients of the quadratic equation. Not all quadratic equations have integer factors; many have irrational or complex roots that cannot be expressed as simple integer factors.
Q2: What if the discriminant is negative?
A2: A negative discriminant indicates that the quadratic equation has two complex roots, which involve the imaginary unit i (√-1). These roots are not represented on the real number line and require the use of complex numbers to express them.
Q3: Which method is the best for solving quadratic equations?
A3: While factoring is the quickest when possible, the quadratic formula is the most reliable and universally applicable method. Completing the square is useful for understanding the process of deriving the quadratic formula and is sometimes helpful for specific problem types.
Q4: How can I check if my solutions are correct?
A4: Substitute the calculated values of x back into the original equation (x² + 7x + 5 = 0). If the equation holds true for both values, your solutions are correct.
Conclusion
The seemingly simple quadratic expression x² + 7x + 5 opens a world of mathematical exploration. Through factoring, completing the square, and the quadratic formula, we can efficiently solve for x and gain insights into the nature of the roots. The graphical representation further clarifies these solutions. Understanding quadratic equations is fundamental to solving various real-world problems across numerous scientific and engineering disciplines, highlighting their significance beyond the classroom. This comprehensive exploration hopefully provides a solid foundation for understanding and applying this crucial mathematical concept.
Latest Posts
Latest Posts
-
Weight Is Vector Or Scalar
Sep 13, 2025
-
Sexual Reproduction Advantages And Disadvantages
Sep 13, 2025
-
Square Root Of 5 3
Sep 13, 2025
-
4 X 3 X 4
Sep 13, 2025
-
What Are Horizontal Rows Called
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about X 2 7 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.