Square Root Of 5 3
thesills
Sep 13, 2025 · 5 min read
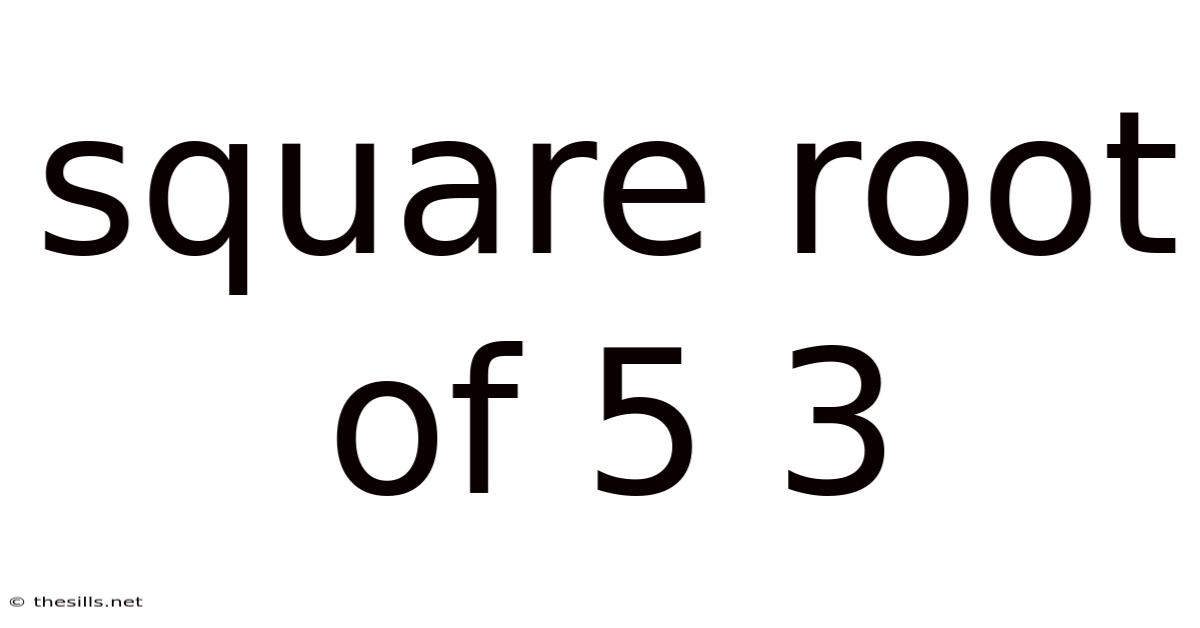
Table of Contents
Decoding the Mystery: Understanding the Square Root of 53
The square root of 53, denoted as √53, might seem like a simple mathematical concept, but it opens doors to a fascinating exploration of number theory, approximation techniques, and the beauty of irrational numbers. This article delves deep into the intricacies of √53, providing a comprehensive understanding suitable for both beginners and those seeking a more advanced perspective. We'll explore its properties, methods for approximating its value, and its significance within broader mathematical contexts. This exploration will demystify this seemingly simple concept, revealing its rich mathematical significance.
Introduction: What is √53?
The square root of a number is a value that, when multiplied by itself, gives the original number. In simpler terms, if x² = 53, then x = √53. Unlike the square root of perfect squares (like √9 = 3 or √16 = 4), √53 is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers) and its decimal representation continues infinitely without repeating. This characteristic makes approximating its value crucial for practical applications.
Methods for Approximating √53
Several methods exist for approximating the square root of 53. These methods vary in complexity and accuracy. Let's examine some popular techniques:
1. Babylonian Method (or Heron's Method): This iterative method refines an initial guess to progressively achieve a more accurate approximation.
- Step 1: Initial Guess: Start with an initial guess, x₀. A reasonable guess for √53 could be 7, since 7² = 49, which is close to 53.
- Step 2: Iteration: Apply the iterative formula: xₙ₊₁ = (xₙ + 53/xₙ) / 2. This formula averages the current guess (xₙ) with the result of dividing 53 by the current guess.
- Step 3: Repetition: Repeat Step 2 until the desired level of accuracy is achieved. The difference between successive approximations will get smaller with each iteration.
Let's perform a few iterations:
- x₀ = 7
- x₁ = (7 + 53/7) / 2 ≈ 7.214
- x₂ = (7.214 + 53/7.214) / 2 ≈ 7.280
- x₃ = (7.280 + 53/7.280) / 2 ≈ 7.280
As you can see, the value converges quickly to approximately 7.280.
2. Linear Approximation: This simpler method uses the tangent line of the function f(x) = √x at a nearby point to approximate the value. Using the point (49, 7), we can find the tangent line's equation and use it to estimate √53.
- The derivative of f(x) = √x is f'(x) = 1/(2√x).
- At x = 49, the slope is f'(49) = 1/(2√49) = 1/14.
- The equation of the tangent line is: y - 7 = (1/14)(x - 49).
- Substituting x = 53, we get y ≈ 7.286.
3. Using a Calculator: Modern calculators provide the most straightforward method. Simply input √53 and the calculator will provide a highly accurate decimal approximation, usually to several decimal places (e.g., 7.280109889...).
The Irrational Nature of √53: A Deeper Dive
The fact that √53 is irrational is a consequence of the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely factorized into prime numbers. If √53 were rational, it could be expressed as a fraction a/b, where a and b are integers with no common factors. This would imply that 53 = (a/b)², or 53b² = a². This equation indicates that a² is divisible by 53. Since 53 is a prime number, a must also be divisible by 53. We can rewrite a as 53k, where k is an integer. Substituting this back into the equation: 53b² = (53k)² = 53²k². This simplifies to b² = 53k². By the same logic, b must also be divisible by 53. This contradicts our initial assumption that a and b have no common factors. Therefore, √53 cannot be expressed as a fraction and must be irrational.
√53 in Geometry and Other Applications
The square root of 53 appears in various geometric and mathematical contexts:
-
Right-Angled Triangles: If a right-angled triangle has legs of length a and b, and hypotenuse c, then by the Pythagorean theorem, c² = a² + b². If we know two sides, we can find the third using this theorem, and √53 could be the solution in certain scenarios. For example, if a = 2 and b = 7, then c = √(2² + 7²) = √53.
-
Coordinate Geometry: Distances between points in a Cartesian coordinate system often involve square roots. The distance between two points (x₁, y₁) and (x₂, y₂) is given by the formula: √((x₂ - x₁)² + (y₂ - y₁)²) and √53 might be the result of such a calculation.
-
Physics and Engineering: Many physics and engineering formulas involve square roots, and √53 could appear as a result of calculations related to velocity, energy, or other physical quantities.
Frequently Asked Questions (FAQs)
- Q: Is √53 a real number?
A: Yes, √53 is a real number. Real numbers encompass all numbers on the number line, including rational and irrational numbers.
- Q: How many decimal places are needed for an accurate approximation of √53?
A: The required number of decimal places depends on the application. For most practical purposes, a few decimal places (e.g., 7.280) provide sufficient accuracy. However, for highly precise calculations, more decimal places may be necessary.
- Q: Can √53 be simplified?
A: No, √53 cannot be simplified because 53 is a prime number. It has no perfect square factors.
- Q: What is the relationship between √53 and other irrational numbers?
A: √53, like other irrational numbers, is a non-repeating, non-terminating decimal. It belongs to the set of real numbers but is not a rational number. Its relationship to other irrational numbers is primarily defined through its position on the real number line and its algebraic properties.
Conclusion: The Significance of Understanding √53
While seemingly a simple concept, understanding the square root of 53 offers valuable insights into the broader world of mathematics. Exploring its irrational nature, employing different approximation techniques, and recognizing its applications in various fields highlight the interconnectedness and depth within even the most basic mathematical concepts. The journey to understanding √53 enhances our appreciation for the elegance and complexity inherent in the mathematical landscape. The process of approximating its value underscores the importance of numerical methods and iterative processes in solving mathematical problems, while the understanding of its irrational nature deepens our comprehension of number theory. This seemingly straightforward number provides a valuable stepping stone towards a more profound understanding of mathematics as a whole. Through this exploration, we've not only calculated the approximate value of √53 but also unravelled some of the fascinating mathematical principles behind it.
Latest Posts
Latest Posts
-
Volume Of The Chamber Decreasing
Sep 13, 2025
-
Maximum Displacement Of A Wave
Sep 13, 2025
-
Al2 So4 3 Percent Composition
Sep 13, 2025
-
Solve X 5 2 3
Sep 13, 2025
-
Freezing Point Depression Constant Formula
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 5 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.