Solve X 5 2 3
thesills
Sep 13, 2025 · 6 min read
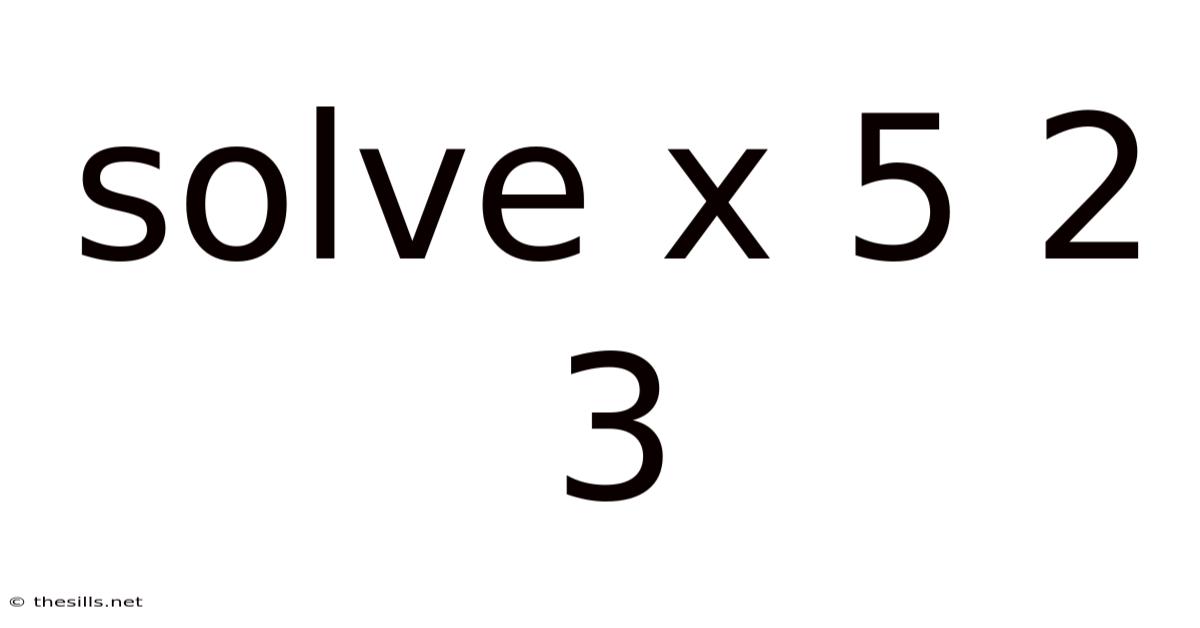
Table of Contents
Solving the Equation: x⁵ + 2x = 3
This article will comprehensively explore how to solve the equation x⁵ + 2x = 3. This seemingly simple equation, involving a fifth-degree polynomial, presents a fascinating challenge that requires a blend of algebraic manipulation, numerical methods, and a touch of intuition. We'll delve into different approaches, from attempting analytical solutions to employing iterative numerical techniques. Understanding this problem provides valuable insight into solving higher-order polynomial equations, a crucial topic in algebra and various branches of mathematics and engineering.
Understanding the Problem: x⁵ + 2x = 3
Our goal is to find the values of 'x' that satisfy the equation x⁵ + 2x = 3. This is a quintic equation (an equation where the highest power of the variable is 5). Unlike quadratic equations (x²), which have straightforward solutions using the quadratic formula, quintic equations often lack elegant, closed-form solutions. This means we may not be able to express the solution using a finite number of basic arithmetic operations and radicals.
Attempting an Analytical Solution
The first approach many might try is to rearrange the equation into a standard polynomial form:
x⁵ + 2x - 3 = 0
We could attempt to factor this polynomial. Unfortunately, finding factors for higher-order polynomials is significantly more challenging than for quadratics. While there are methods for finding rational roots (the Rational Root Theorem), they don't guarantee a solution, and in this case, they won't lead to a complete factorization. We can test integer values:
- If x = 1: 1⁵ + 2(1) - 3 = 0. Therefore, x = 1 is a root.
This means (x - 1) is a factor. We can perform polynomial long division or synthetic division to find the remaining polynomial:
(x⁵ + 2x - 3) ÷ (x - 1) = x⁴ + x³ + x² + x + 3
Now we are left with a quartic equation: x⁴ + x³ + x² + x + 3 = 0. Finding the roots of this quartic equation analytically is still quite complex and often impossible without resorting to numerical methods. There isn't a simple quartic formula equivalent to the quadratic formula.
Numerical Methods for Solving x⁴ + x³ + x² + x + 3 = 0
Since an analytical solution is impractical for the quartic equation, we turn to numerical methods. These methods iteratively approximate the roots of the equation. Several techniques are available:
-
Newton-Raphson Method: This iterative method uses the derivative of the function to refine the approximation of a root. The formula is:
x_(n+1) = x_n - f(x_n) / f'(x_n)
Where:
- x_n is the current approximation
- x_(n+1) is the next approximation
- f(x) is the function (x⁴ + x³ + x² + x + 3)
- f'(x) is the derivative of the function (4x³ + 3x² + 2x + 1)
To use this method, we need an initial guess for x. We can start with, say, x₀ = -1.5. We then iteratively apply the formula until the difference between successive approximations becomes sufficiently small.
-
Bisection Method: This method repeatedly bisects an interval known to contain a root. It's simpler than Newton-Raphson but converges slower. It requires finding an interval [a, b] where f(a) and f(b) have opposite signs. The midpoint of the interval is then tested, and the interval is halved based on the sign of f(midpoint).
-
Secant Method: This method is similar to the Newton-Raphson method but approximates the derivative using the slope between two points. It requires two initial guesses.
Applying the Newton-Raphson Method (Example)
Let's demonstrate the Newton-Raphson method with an initial guess of x₀ = -1.5.
-
Iteration 1:
- f(-1.5) = (-1.5)⁴ + (-1.5)³ + (-1.5)² + (-1.5) + 3 ≈ 1.3125
- f'(-1.5) = 4(-1.5)³ + 3(-1.5)² + 2(-1.5) + 1 ≈ -8.25
- x₁ = -1.5 - (1.3125 / -8.25) ≈ -1.338
-
Iteration 2:
- f(-1.338) ≈ 0.264
- f'(-1.338) ≈ -6.38
- x₂ ≈ -1.338 - (0.264 / -6.38) ≈ -1.334
We continue this process until we reach a desired level of accuracy. After several more iterations, we would find an approximation for one of the real roots of the quartic equation. Note that quartic equations can have up to four real roots or a mixture of real and complex roots.
Finding Other Roots
The numerical methods mentioned above will only find one root at a time. To find other roots, we can use different starting points for the iterative methods or employ techniques such as deflation (dividing the original polynomial by the factor corresponding to the found root to obtain a lower-degree polynomial). The process can be computationally intensive, particularly for higher-order polynomials. Sophisticated software packages are commonly used for solving such equations accurately and efficiently.
Complex Roots
It's important to remember that quintic equations can have complex roots (roots involving the imaginary unit i). Numerical methods can still approximate these complex roots, but the interpretation and handling of complex numbers become more involved.
Graphical Interpretation
Graphing the function y = x⁵ + 2x - 3 can provide valuable insights. The x-intercepts of the graph represent the real roots of the equation. We can use graphing software or calculators to visualize the function and obtain approximate values of the roots. The graph will clearly show the root at x = 1, and potentially suggest the approximate locations of other roots.
Frequently Asked Questions (FAQ)
-
Q: Are there always analytical solutions for quintic equations? A: No. The Abel-Ruffini theorem proves that there's no general algebraic solution for polynomial equations of degree five or higher using only radicals.
-
Q: Which numerical method is best? A: The optimal numerical method depends on factors like the desired accuracy, the initial guess, and the characteristics of the function. Newton-Raphson generally converges faster if a good initial guess is available, but it might diverge if the guess is poor. The bisection method is more robust but converges slower.
-
Q: Can I solve this using a calculator or computer software? A: Yes, many calculators and computer algebra systems (like MATLAB, Mathematica, or even online calculators) have built-in functions or routines to solve polynomial equations numerically. These tools are highly recommended for practical applications.
-
Q: What are the applications of solving such equations? A: Solving higher-order polynomial equations has numerous applications in various fields, including engineering (e.g., determining stability of systems, analyzing oscillations), physics (e.g., solving equations of motion), and computer graphics (e.g., curve fitting).
Conclusion
Solving the equation x⁵ + 2x = 3, while seemingly simple, demonstrates the complexities inherent in solving higher-order polynomial equations. While an analytical solution for the complete equation is impractical, we can find one root directly (x=1) and then use numerical methods like Newton-Raphson, Bisection, or Secant methods to approximate the remaining roots. Understanding these techniques provides crucial skills in mathematics and engineering, emphasizing the power of both analytical approaches and the necessity of numerical methods when dealing with complex mathematical problems. Remember to always leverage computational tools to find precise and efficient solutions in practical applications.
Latest Posts
Latest Posts
-
What Is 12 Of 75000
Sep 13, 2025
-
On And Off Light Switch
Sep 13, 2025
-
What Is Freezing Point Fahrenheit
Sep 13, 2025
-
Properties Of The Scalar Product
Sep 13, 2025
-
Does Tap Water Conduct Electricity
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Solve X 5 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.