4 X 3 X 4
thesills
Sep 13, 2025 · 6 min read
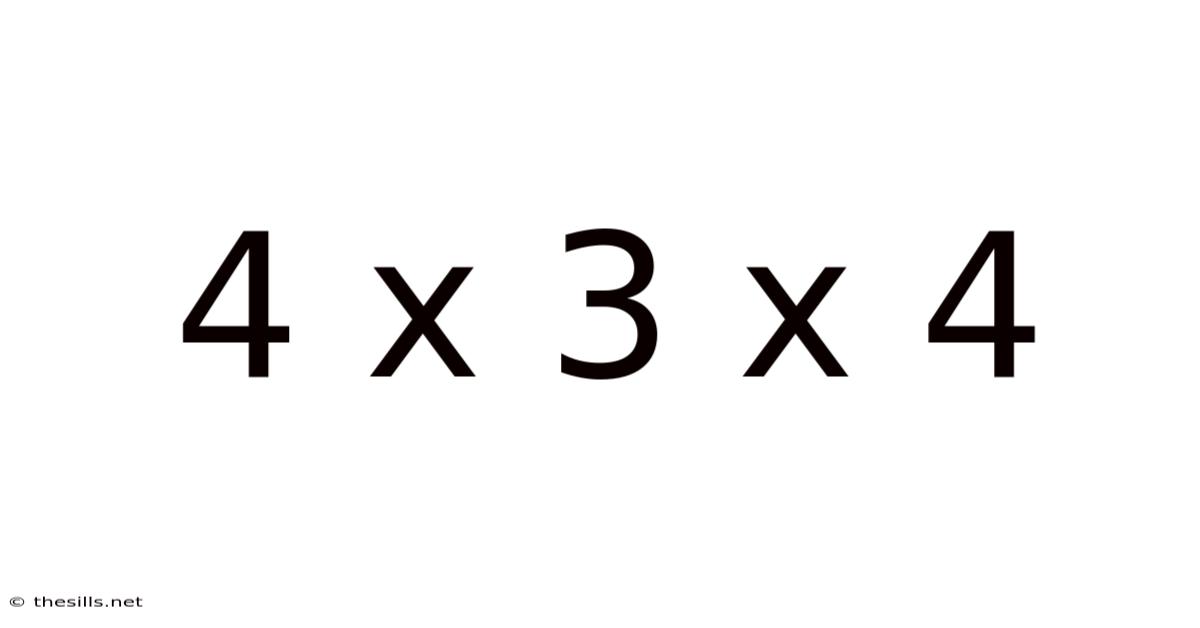
Table of Contents
Decoding 4 x 3 x 4: Exploring Dimensions, Volume, and Beyond
This article delves into the seemingly simple mathematical expression "4 x 3 x 4," exploring its implications beyond basic multiplication. We'll unpack its significance in various contexts, from calculating volumes to understanding spatial reasoning and even touching upon its abstract mathematical interpretations. This seemingly straightforward equation opens doors to a surprisingly rich world of mathematical concepts. Let's begin!
Understanding the Fundamentals: Multiplication and Dimensions
At its core, "4 x 3 x 4" represents a multiplication problem. In the simplest terms, it means multiplying four by three, and then multiplying the result by four. The answer, 48, is straightforward to calculate. However, the true power of this expression lies in its ability to represent something beyond a simple numerical result: dimensions.
The numbers in the equation—4, 3, and 4—can be interpreted as representing the lengths of the sides of a three-dimensional rectangular prism (or cuboid). Imagine a box: one side measures 4 units long, another 3 units wide, and the third 4 units high. The multiplication then calculates the volume of this box.
This leads us to the concept of volume. Volume is a measure of the three-dimensional space occupied by an object. It's essentially how much "stuff" can fit inside. For our rectangular prism, the volume calculation "4 x 3 x 4 = 48" tells us that it has a volume of 48 cubic units. The "cubic units" part is crucial; it indicates that the volume is measured in three dimensions.
Applications in Real-World Scenarios
The concept of calculating volume using multiplication, as illustrated by "4 x 3 x 4," has countless real-world applications. Here are a few examples:
-
Construction and Architecture: Architects and builders use these calculations to determine the amount of materials needed for various projects. For instance, calculating the volume of a room helps determine the amount of paint needed for the walls or the amount of concrete required for a foundation. Larger structures such as warehouses or buildings rely on similar calculations, but with much larger dimensions.
-
Packaging and Shipping: Companies that manufacture and ship goods use volume calculations extensively. Knowing the volume of a package allows them to determine the shipping costs and ensure the package fits within shipping containers or trucks. Optimizing package sizes to minimize wasted space is a crucial element in logistics and cost efficiency.
-
Engineering: Engineers use volume calculations in a broad range of applications. For example, determining the capacity of a water tank, calculating the amount of fuel a car's tank can hold, or assessing the size of a storage silo for grains all rely on accurately determining volume using three-dimensional measurements.
-
Agriculture: Farmers utilize volume calculations to understand the capacity of silos, barns, and irrigation systems. Accurate calculations ensure efficient storage and distribution of crops and water, crucial for maximizing yield and managing resources.
Expanding the Concept: Beyond Rectangular Prisms
While we've focused on rectangular prisms, the fundamental principle of multiplying dimensions to find volume applies to other shapes, although the calculations may become more complex. For instance:
-
Cylinders: The volume of a cylinder is calculated using the formula πr²h, where 'r' is the radius and 'h' is the height. While the calculation is different, the underlying concept of multiplying dimensions to find the volume remains the same.
-
Spheres: The volume of a sphere is calculated using (4/3)πr³. Again, different formula but the same principle – three dimensional space is quantified by multiplying certain dimensions.
-
Irregular Shapes: Calculating the volume of irregular shapes is more challenging and often requires techniques like water displacement or numerical integration.
Mathematical Extensions and Abstract Interpretations
The seemingly simple expression "4 x 3 x 4" also opens doors to more complex mathematical concepts:
-
Matrices and Linear Algebra: In linear algebra, numbers can be arranged into matrices, which are rectangular arrays of numbers. Matrix multiplication involves operations similar to what we see in "4 x 3 x 4," but extended to multiple dimensions.
-
Tensor Calculus: This branch of mathematics deals with tensors, which are multi-dimensional arrays that generalize vectors and matrices. Tensor calculus is vital in physics, particularly in general relativity and quantum mechanics, where it’s used to represent physical quantities.
-
Abstract Algebra: The multiplicative nature of "4 x 3 x 4" resonates with the concept of group theory in abstract algebra, which studies algebraic structures with operations that obey certain rules.
Frequently Asked Questions (FAQs)
Q: What are the units involved in the calculation 4 x 3 x 4?
A: The units depend on the context. If the dimensions (4, 3, and 4) are measured in centimeters (cm), then the volume will be in cubic centimeters (cm³). Similarly, if the dimensions are in meters (m), the volume will be in cubic meters (m³), and so on. The crucial point is that the volume is always expressed in cubic units.
Q: Can the order of numbers in "4 x 3 x 4" be changed?
A: Yes, due to the commutative property of multiplication, the order of the numbers can be changed without affecting the result. 4 x 3 x 4 is the same as 3 x 4 x 4, 4 x 4 x 3, and so on. The volume remains 48 cubic units regardless of the order.
Q: What if one of the numbers is zero?
A: If any of the numbers in the expression is zero, the entire product will be zero. This makes intuitive sense because a box with zero length, width, or height will have zero volume.
Q: What if the numbers are decimals or fractions?
A: The same principles apply. If the dimensions are given as decimals or fractions, the volume will be calculated using the same multiplication process, yielding a result in cubic units that reflects the fractional or decimal nature of the dimensions.
Q: How does this relate to surface area?
A: While this article focuses on volume, it's important to distinguish it from surface area. Surface area is the total area of all the surfaces of a three-dimensional object. For a rectangular prism, the surface area is calculated using a different formula, involving the lengths of all its sides.
Conclusion: The Richness of a Simple Equation
The seemingly simple mathematical expression "4 x 3 x 4" reveals a wealth of mathematical concepts and real-world applications. From calculating the volume of everyday objects to understanding complex mathematical principles, this equation serves as a gateway to appreciating the power and elegance of mathematics. Its significance extends beyond a simple numerical result, highlighting the interconnectedness of mathematics with various aspects of our lives and the universe around us. The seemingly simple act of multiplication unlocks a world of spatial reasoning, problem-solving, and abstract mathematical exploration. So next time you encounter a simple multiplication problem, remember the depth and breadth of understanding that it can reveal.
Latest Posts
Latest Posts
-
How Long Is 420 Months
Sep 13, 2025
-
Does Density Change With Size
Sep 13, 2025
-
Largest Circle In A Square
Sep 13, 2025
-
Volume Of The Chamber Decreasing
Sep 13, 2025
-
Maximum Displacement Of A Wave
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 4 X 3 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.