Square Root Of 98 Simplified
thesills
Sep 14, 2025 · 5 min read
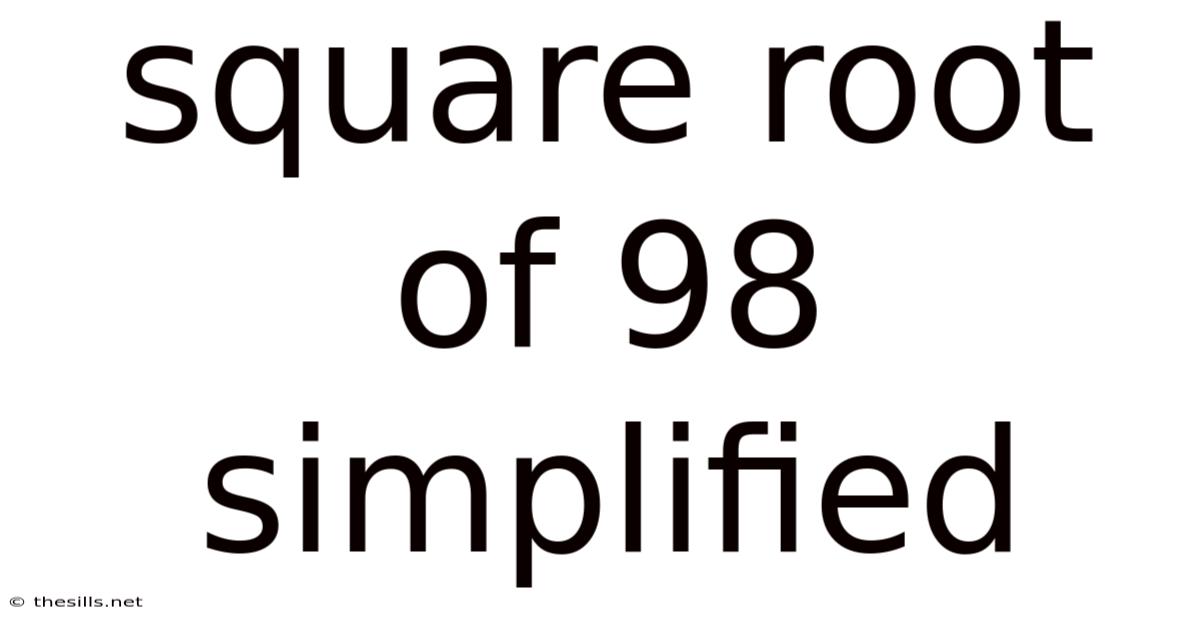
Table of Contents
Simplifying the Square Root of 98: A Comprehensive Guide
Finding the square root of 98 might seem like a straightforward task, but simplifying the answer reveals a deeper understanding of mathematical principles. This comprehensive guide will walk you through the process of simplifying √98, explaining the underlying concepts and offering additional insights into square root simplification. We'll delve into the prime factorization method, demonstrate how to handle different types of square roots, and even explore the historical context of these mathematical concepts. By the end, you'll not only know the simplified form of √98 but also possess the tools to tackle similar problems with confidence.
Understanding Square Roots
Before diving into the simplification of √98, let's refresh our understanding of square roots. A square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. Square roots are essentially the inverse operation of squaring a number. However, not all square roots result in whole numbers. Many square roots, like √98, produce irrational numbers – numbers that cannot be expressed as a simple fraction. This is where simplification becomes crucial.
Prime Factorization: The Key to Simplification
The most effective method for simplifying square roots like √98 is through prime factorization. Prime factorization involves breaking down a number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this to 98:
- Find the prime factors of 98: We start by dividing 98 by the smallest prime number, 2: 98 ÷ 2 = 49.
- Continue factoring: 49 is not divisible by 2, but it is divisible by 7: 49 ÷ 7 = 7. 7 is a prime number, so we've reached the end of our factorization.
- Express 98 as a product of its prime factors: Therefore, 98 = 2 x 7 x 7, or 2 x 7².
Simplifying √98 using Prime Factorization
Now that we've expressed 98 as 2 x 7², we can rewrite √98 as √(2 x 7²). The key to simplification lies in recognizing that √(a x b) = √a x √b. Applying this rule, we get:
√(2 x 7²) = √2 x √7²
Since √7² = 7 (because 7 x 7 = 49), our simplified expression becomes:
7√2
Therefore, the simplified form of √98 is 7√2. This means that 7√2, when multiplied by itself, will equal 98.
Visualizing the Simplification
Imagine a square with an area of 98 square units. We're trying to find the length of one side of this square. By factoring 98 into 2 x 7², we can visualize this square as a rectangle with sides of length 7 and 7√2. The area of this rectangle is indeed 7 x 7√2 = 49√2, which is approximately 98. This visual representation helps solidify the concept of simplification.
Handling Different Types of Square Roots
The method we used for √98 applies to a wide range of square roots. Let's consider some examples:
-
√12: Prime factorization of 12 is 2² x 3. Therefore, √12 = √(2² x 3) = √2² x √3 = 2√3.
-
√75: Prime factorization of 75 is 3 x 5². Therefore, √75 = √(3 x 5²) = √3 x √5² = 5√3.
-
√147: Prime factorization of 147 is 3 x 7². Therefore, √147 = √(3 x 7²) = √3 x √7² = 7√3
-
√200: Prime factorization of 200 is 2³ x 5². Therefore, √200 = √(2³ x 5²) = √(2² x 2 x 5²) = √2² x √5² x √2 = 10√2
These examples illustrate the consistent application of prime factorization and the rule √(a x b) = √a x √b for simplifying various square roots.
Beyond Simplification: Approximating Irrational Numbers
While 7√2 is the simplified form, it's still an irrational number. To find its approximate decimal value, we can use a calculator: 7√2 ≈ 9.899. This approximation helps us understand the magnitude of the square root.
Historical Context: The Evolution of Square Roots
The concept of square roots has a rich history, dating back to ancient civilizations. Babylonian mathematicians, as early as the 2nd millennium BC, developed methods for approximating square roots. The Greeks, particularly Pythagoras and his followers, explored the relationship between numbers and geometry, furthering our understanding of square roots and their geometric interpretations. The development of algebra and calculus further refined the techniques for working with and calculating square roots.
Frequently Asked Questions (FAQ)
Q: Why is prime factorization important in simplifying square roots?
A: Prime factorization allows us to identify perfect squares within the number, which can then be extracted from the square root, leading to a simplified expression. Without prime factorization, simplification would be significantly more difficult, if not impossible.
Q: Can all square roots be simplified?
A: No. Square roots of perfect squares (like √16 = 4) simplify to whole numbers. However, square roots of numbers that are not perfect squares (like √98) can be simplified to a form containing a radical, but they remain irrational numbers.
Q: What if I get a negative number inside the square root?
A: The square root of a negative number is not a real number. It involves imaginary numbers, represented by the symbol 'i', where i² = -1. This is a topic explored in more advanced mathematics.
Q: Are there other methods to simplify square roots?
A: While prime factorization is the most efficient and widely used method, other approaches exist, but they often rely on prior knowledge of perfect squares or involve more complex calculations. Prime factorization provides a systematic and universally applicable approach.
Conclusion
Simplifying the square root of 98, or any square root for that matter, is a fundamental skill in mathematics. By mastering the technique of prime factorization, you equip yourself with a powerful tool for simplifying radical expressions. This process not only provides a concise and mathematically correct answer (7√2 in this case) but also enhances your understanding of fundamental mathematical concepts and their applications. Remember that simplification is about expressing the answer in its most efficient and manageable form, while retaining its mathematical integrity. The process, explained here in detail, not only provides the answer but illustrates the logical steps and the underlying principles, making it easier for you to solve similar problems independently and with confidence. So go ahead, try simplifying other square roots, and watch your mathematical skills flourish!
Latest Posts
Latest Posts
-
15 Inches By 15 Inches
Sep 14, 2025
-
Factor 3x 2 11x 6
Sep 14, 2025
-
Factor 2x 2 X 10
Sep 14, 2025
-
No Ball Rules In Cricket
Sep 14, 2025
-
What Tools To Measure Mass
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 98 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.