Factor 2x 2 X 10
thesills
Sep 14, 2025 · 6 min read
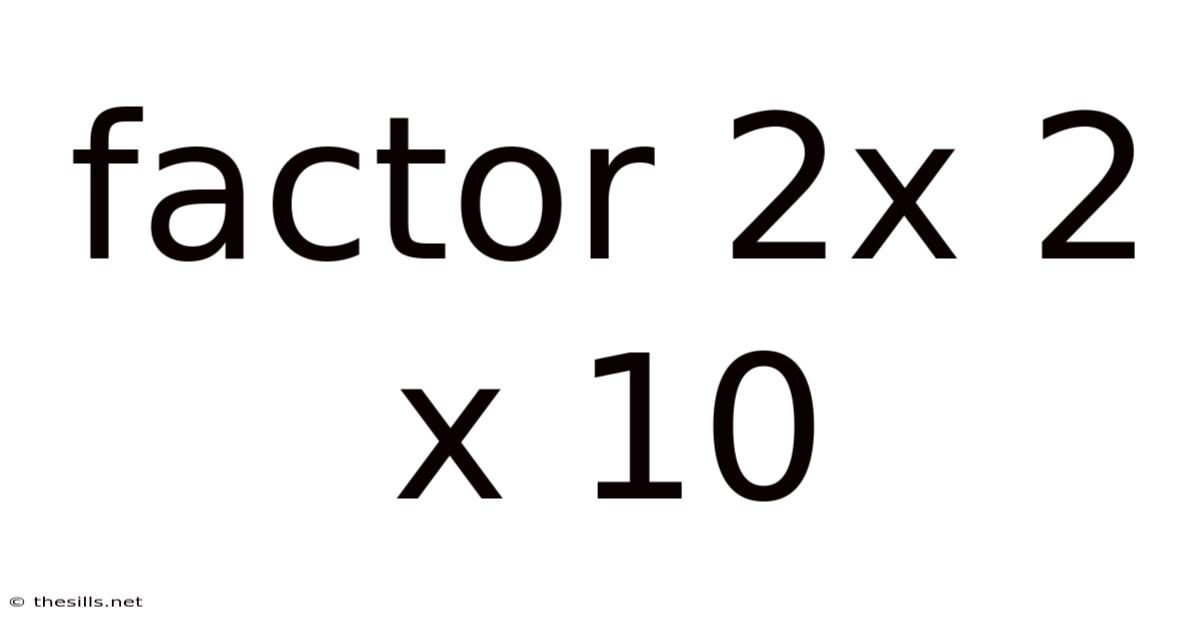
Table of Contents
Decoding 2 x 2 x 10: A Deep Dive into Factorization and its Applications
This article explores the seemingly simple mathematical expression "2 x 2 x 10," delving beyond the immediate answer to uncover the underlying principles of factorization, its practical applications, and its connections to broader mathematical concepts. We will dissect this expression, examining its prime factorization, its relevance in different mathematical fields, and its implications in real-world problem-solving. Understanding this simple equation lays the foundation for grasping more complex mathematical operations and concepts.
Understanding Factorization: Breaking Down Numbers
Factorization, at its core, is the process of breaking down a number into smaller numbers that, when multiplied together, produce the original number. These smaller numbers are called factors. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12, because 1 x 12 = 12, 2 x 6 = 12, and 3 x 4 = 12. In our case, we're examining the factorization of the result of 2 x 2 x 10. Let's first calculate the product:
2 x 2 x 10 = 40
Now, we can explore the factorization of 40.
Prime Factorization of 40: The Building Blocks
Prime factorization is a specific type of factorization where a number is expressed as a product of only prime numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...). Prime factorization is unique for every number, meaning there's only one way to express a number as a product of prime numbers (ignoring the order of the factors).
To find the prime factorization of 40, we can use a factor tree:
40
/ \
2 20
/ \
2 10
/ \
2 5
Following the branches, we see that 40 can be expressed as 2 x 2 x 2 x 5. This is its prime factorization. We can write this more concisely using exponents: 2³ x 5. This representation highlights the fundamental building blocks of the number 40. This process is crucial in various mathematical operations, especially simplifying fractions and solving equations.
Beyond the Basics: Applications of Factorization
The seemingly simple act of factorization has far-reaching implications across numerous areas of mathematics and beyond:
1. Simplifying Fractions:
Factorization is essential for simplifying fractions to their lowest terms. For example, consider the fraction 40/60. By factoring both the numerator (40) and the denominator (60), we can simplify:
40 = 2³ x 5 60 = 2² x 3 x 5
Therefore, 40/60 can be written as (2³ x 5) / (2² x 3 x 5). We can cancel out common factors (2² and 5) from both the numerator and denominator, leaving us with 2/3.
2. Solving Equations:
Factorization plays a vital role in solving polynomial equations. Consider a quadratic equation like x² + 7x + 12 = 0. Factoring the quadratic expression allows us to find the roots (solutions) of the equation. In this case, the expression factors to (x + 3)(x + 4) = 0, meaning the solutions are x = -3 and x = -4.
3. Greatest Common Divisor (GCD) and Least Common Multiple (LCM):
Factorization is the key to efficiently calculating the GCD and LCM of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder, while the LCM is the smallest number that is a multiple of all the given numbers. By comparing the prime factorizations of numbers, we can easily determine their GCD and LCM. For example, let's find the GCD and LCM of 40 and 60:
40 = 2³ x 5 60 = 2² x 3 x 5
GCD(40, 60) = 2² x 5 = 20 (we take the lowest power of common prime factors) LCM(40, 60) = 2³ x 3 x 5 = 120 (we take the highest power of all prime factors)
4. Cryptography:
Prime factorization is at the heart of many modern encryption algorithms. The difficulty of factoring very large numbers into their prime components forms the basis of the security of these systems. This is because while multiplying two large prime numbers is relatively easy, factoring their product back into the original primes is computationally extremely intensive.
5. Modular Arithmetic and Number Theory:
Factorization is fundamental in number theory, a branch of mathematics focused on the properties of integers. Concepts like modular arithmetic, used extensively in cryptography and computer science, rely heavily on prime factorization and the understanding of divisors.
Real-World Applications: From Packaging to Programming
The mathematical principles behind factorization extend beyond abstract theory; they have tangible applications in various real-world scenarios:
-
Packaging and Logistics: Optimizing package sizes often involves finding factors to efficiently use space and materials. For example, a company might need to determine the dimensions of a box that can hold a specific number of items, requiring knowledge of factors and divisors.
-
Construction and Engineering: Factorization helps in calculating measurements and proportions in construction projects, ensuring structural integrity and efficient resource allocation.
-
Computer Science and Programming: Factorization algorithms are used in various computer science applications, including cryptography, data compression, and database management. Understanding prime factorization is crucial for developing efficient and secure software.
-
Scheduling and Time Management: Finding common multiples (using LCM) is essential for scheduling tasks or events that need to occur at regular intervals.
Frequently Asked Questions (FAQ)
Q: What is the difference between factorization and prime factorization?
A: Factorization is the general process of breaking down a number into smaller numbers that multiply to give the original number. Prime factorization is a specific type of factorization where the number is expressed as a product of only prime numbers.
Q: Is there only one prime factorization for a number?
A: Yes, the fundamental theorem of arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers (disregarding the order of the factors).
Q: Why is prime factorization important in cryptography?
A: The difficulty of factoring very large numbers into their prime components is the foundation of the security of many modern encryption algorithms. The computational cost of factoring large numbers makes it practically impossible to break these systems.
Q: How can I improve my factorization skills?
A: Practice is key! Start with smaller numbers and gradually increase the complexity. Use factor trees and learn to recognize common factors and prime numbers. There are also many online resources and exercises available to help you hone your factorization skills.
Conclusion: The Enduring Power of a Simple Equation
While seemingly straightforward, the equation 2 x 2 x 10 = 40, and its subsequent prime factorization (2³ x 5), provides a gateway to understanding fundamental mathematical concepts like factorization, prime numbers, and their far-reaching implications. From simplifying fractions to securing online transactions, the ability to factor numbers efficiently is a valuable tool across diverse fields. Mastering this seemingly simple process empowers you not only to solve mathematical problems but also to appreciate the elegance and power of fundamental mathematical principles in our everyday lives. It's a testament to how seemingly simple concepts can form the bedrock of complex and fascinating mathematical structures. The journey of understanding 2 x 2 x 10 is just the beginning of a much wider and more enriching mathematical exploration.
Latest Posts
Latest Posts
-
Enthalpy Of Formation Carbon Monoxide
Sep 14, 2025
-
What Is An Anhydrous Salt
Sep 14, 2025
-
Kg Per Meter Second Squared
Sep 14, 2025
-
Vascular Bundles Of Monocot Stem
Sep 14, 2025
-
Non Examples Of Igneous Rocks
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Factor 2x 2 X 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.