Factor 3x 2 11x 6
thesills
Sep 14, 2025 · 6 min read
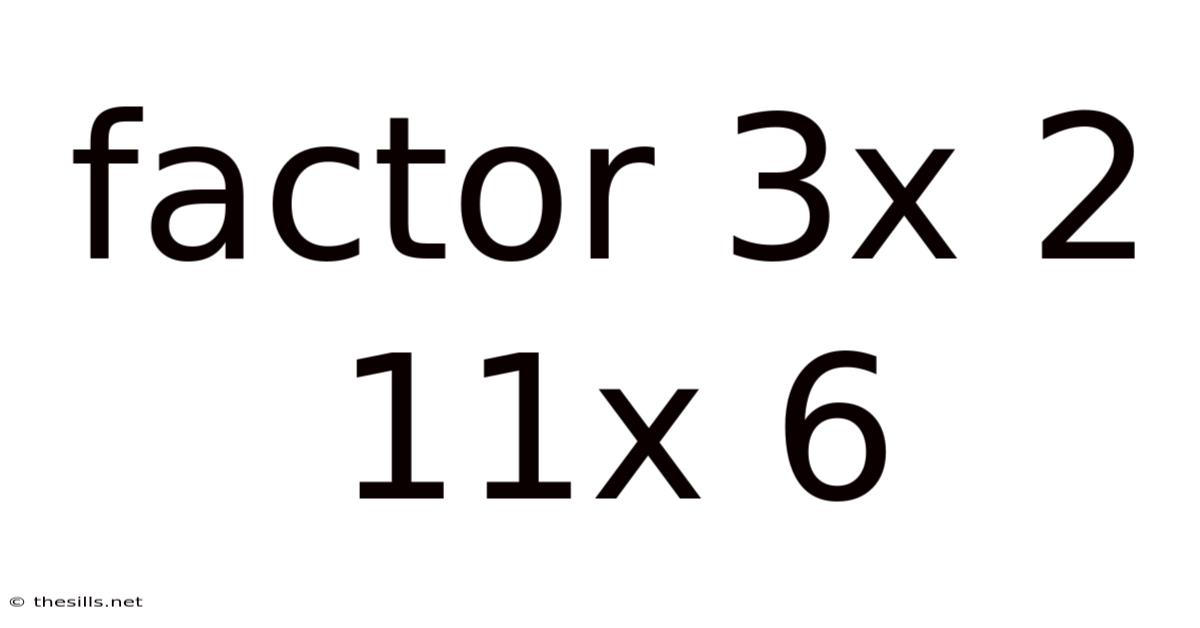
Table of Contents
Factoring the Quadratic Expression 3x² + 11x + 6: A Comprehensive Guide
Factoring quadratic expressions is a fundamental skill in algebra. Understanding how to factor allows you to solve quadratic equations, simplify complex expressions, and delve deeper into the world of polynomial functions. This article provides a thorough explanation of how to factor the quadratic expression 3x² + 11x + 6, covering various methods and offering insights into the underlying mathematical principles. We'll move beyond simply finding the answer and explore the 'why' behind each step, making this process clear and understandable for students of all levels.
Understanding Quadratic Expressions
Before diving into the factoring process, let's briefly review what a quadratic expression is. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. It generally takes the form ax² + bx + c, where 'a', 'b', and 'c' are constants (numbers). In our case, a = 3, b = 11, and c = 6. Our goal is to rewrite this expression as a product of two simpler expressions, typically two binomials.
Method 1: AC Method (Product-Sum Method)
The AC method, also known as the product-sum method, is a widely used technique for factoring quadratic expressions. It's particularly helpful when the coefficient of x² (the 'a' value) is not 1.
Steps:
-
Find the product 'ac': Multiply the coefficient of x² (a) by the constant term (c). In our example, ac = 3 * 6 = 18.
-
Find two numbers that add up to 'b' and multiply to 'ac': We need two numbers that add up to 11 (the coefficient of x, which is 'b') and multiply to 18. These numbers are 9 and 2 (9 + 2 = 11 and 9 * 2 = 18).
-
Rewrite the middle term: Replace the middle term (11x) with the two numbers we found, keeping the x variable: 3x² + 9x + 2x + 6.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
- 3x(x + 3) + 2(x + 3)
-
Factor out the common binomial: Notice that both terms now share the common binomial (x + 3). Factor this out: (x + 3)(3x + 2).
Therefore, the factored form of 3x² + 11x + 6 is (x + 3)(3x + 2).
Method 2: Trial and Error
This method involves a bit of guesswork and checking, but it can be quicker once you become proficient.
Steps:
-
Set up the binomial factors: Since the coefficient of x² is 3, the first terms in the binomials must multiply to 3x². The possibilities are (3x _)(x _).
-
Find factors of the constant term: The constant term is 6. Its factor pairs are (1, 6), (2, 3), (3, 2), and (6, 1).
-
Test the factor pairs: We need to find a combination that, when multiplied out using the FOIL (First, Outer, Inner, Last) method, results in the original expression. Let's test a few:
- (3x + 1)(x + 6) = 3x² + 18x + x + 6 = 3x² + 19x + 6 (Incorrect)
- (3x + 2)(x + 3) = 3x² + 9x + 2x + 6 = 3x² + 11x + 6 (Correct!)
Therefore, the factored form is again (x + 3)(3x + 2). This method requires more intuition and practice but can be faster for simpler quadratic expressions.
Method 3: Quadratic Formula (Indirect Factoring)
While not a direct factoring method, the quadratic formula can be used to find the roots (solutions) of the quadratic equation 3x² + 11x + 6 = 0. These roots can then be used to determine the factors.
The quadratic formula is: x = [-b ± √(b² - 4ac)] / 2a
Substituting our values (a = 3, b = 11, c = 6):
x = [-11 ± √(11² - 4 * 3 * 6)] / (2 * 3) x = [-11 ± √(121 - 72)] / 6 x = [-11 ± √49] / 6 x = [-11 ± 7] / 6
This gives us two solutions:
x₁ = (-11 + 7) / 6 = -4 / 6 = -2/3 x₂ = (-11 - 7) / 6 = -18 / 6 = -3
The factors are then found by setting each solution equal to x and solving for the expression in parentheses:
- x = -2/3 => 3x = -2 => 3x + 2 = 0
- x = -3 => x + 3 = 0
Therefore, the factors are (3x + 2) and (x + 3), leading to the same factored form: (x + 3)(3x + 2).
The Significance of Factoring
Factoring quadratic expressions is more than just a mathematical manipulation; it's a crucial stepping stone to understanding higher-level concepts. Here's why factoring is important:
-
Solving Quadratic Equations: Setting a quadratic expression equal to zero creates a quadratic equation. Factoring allows you to find the roots (solutions) of the equation by setting each factor equal to zero and solving for x. This is a fundamental technique in various applications, from physics to engineering.
-
Simplifying Expressions: Factoring simplifies complex algebraic expressions, making them easier to manipulate and analyze. This simplification is essential for solving more intricate problems.
-
Graphing Quadratic Functions: The factored form of a quadratic expression reveals the x-intercepts (where the graph crosses the x-axis) of the corresponding quadratic function. This is invaluable for sketching the graph of the function.
-
Understanding Polynomial Behavior: Factoring provides insight into the behavior of polynomial functions. For example, the multiplicity of a root (how many times a factor appears) influences the graph's behavior near the x-intercept.
Frequently Asked Questions (FAQ)
-
What if the quadratic expression cannot be factored? Some quadratic expressions are not factorable using integers. In such cases, the quadratic formula or completing the square can be used to find the roots, which are then expressed as irrational numbers.
-
Is there a specific order for the factors? The order of the factors doesn't matter. (x + 3)(3x + 2) is equivalent to (3x + 2)(x + 3). Both represent the same factored form.
-
Can I use other factoring methods? While the AC method, trial and error, and the quadratic formula are common, other techniques like completing the square can also be used to indirectly obtain the factors. The best method depends on the specific quadratic expression and individual preference.
-
How do I check my answer? Always verify your factored form by expanding it using the FOIL method. If you get back the original quadratic expression, your factoring is correct.
Conclusion
Factoring the quadratic expression 3x² + 11x + 6, whether using the AC method, trial and error, or indirectly through the quadratic formula, ultimately leads to the same factored form: (x + 3)(3x + 2). This article has explored these methods in detail, emphasizing the underlying principles and highlighting the importance of factoring in algebra and beyond. Mastering factoring techniques is a cornerstone of algebraic proficiency, empowering you to tackle more complex problems and gain a deeper understanding of polynomial functions and their applications. Remember practice is key! The more you practice factoring different quadratic expressions, the more comfortable and efficient you will become. Don't hesitate to work through additional examples to solidify your understanding.
Latest Posts
Latest Posts
-
Enthalpy Of Formation Carbon Monoxide
Sep 14, 2025
-
What Is An Anhydrous Salt
Sep 14, 2025
-
Kg Per Meter Second Squared
Sep 14, 2025
-
Vascular Bundles Of Monocot Stem
Sep 14, 2025
-
Non Examples Of Igneous Rocks
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Factor 3x 2 11x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.