Factor 2x 2 1x 1
thesills
Sep 12, 2025 · 5 min read
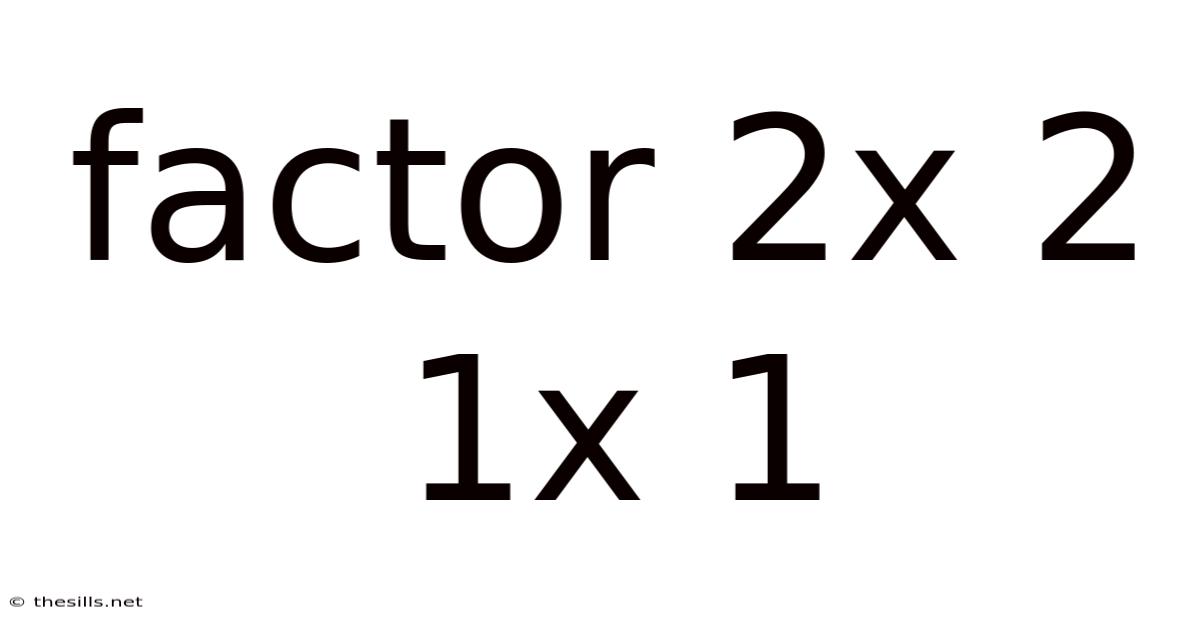
Table of Contents
Decoding the Mystery: A Deep Dive into Factorization of 2x² + 2x + 1
Factoring quadratic expressions is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding a wide range of mathematical concepts. While some quadratics factor easily, others present a greater challenge. This article will delve deep into the factorization of the quadratic expression 2x² + 2x + 1, exploring its properties, attempting different factorization methods, and ultimately determining whether it's possible to factor it using standard techniques. We'll also touch upon more advanced methods and explore the broader context of quadratic factorization.
Introduction: Understanding Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and a ≠ 0. Factoring a quadratic means expressing it as a product of two simpler expressions, usually linear binomials. This process is essential for solving quadratic equations (setting the expression equal to zero and finding the values of x that satisfy the equation).
Attempting Traditional Factoring Methods
Let's try to factor 2x² + 2x + 1 using the common methods:
-
Greatest Common Factor (GCF): The first step in any factoring problem is to check for a greatest common factor among the terms. In this case, there is no common factor (other than 1) among 2x², 2x, and 1.
-
Simple Trinomial Factoring: This method works when the quadratic can be expressed as (px + q)(rx + s), where p, q, r, and s are constants. Expanding this gives prx² + (ps + qr)x + qs. We need to find p, q, r, and s such that pr = 2, ps + qr = 2, and qs = 1. Trying various combinations, we find it’s impossible to find integers that satisfy all three conditions simultaneously.
-
AC Method: For quadratics of the form ax² + bx + c, the AC method involves finding two numbers that multiply to ac and add up to b. In our case, a = 2, b = 2, and c = 1. Therefore, we need two numbers that multiply to 2(1) = 2 and add up to 2. The only integer pairs that multiply to 2 are (1, 2) and (-1, -2), neither of which adds up to 2. Therefore, this method doesn't yield a simple factorization.
The Discriminant and the Quadratic Formula
When simple factoring methods fail, we can turn to the quadratic formula or examine the discriminant. The discriminant (Δ) is the part of the quadratic formula under the square root: Δ = b² - 4ac. It tells us about the nature of the roots (solutions) of the quadratic equation ax² + bx + c = 0.
- Δ > 0: Two distinct real roots.
- Δ = 0: One real root (a repeated root).
- Δ < 0: Two complex roots (roots involving the imaginary unit i, where i² = -1).
For 2x² + 2x + 1, the discriminant is:
Δ = (2)² - 4(2)(1) = 4 - 8 = -4
Since the discriminant is negative, the quadratic equation 2x² + 2x + 1 = 0 has two complex roots. This strongly suggests that the quadratic expression itself cannot be factored using real numbers. We can only factor it using complex numbers.
Factoring with Complex Numbers
To factor 2x² + 2x + 1 using complex numbers, we need to find the roots of the corresponding quadratic equation using the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
Substituting a = 2, b = 2, and c = 1, we get:
x = [-2 ± √(-4)] / 4 = [-2 ± 2i] / 4 = -1/2 ± i/2
The roots are x₁ = -1/2 + i/2 and x₂ = -1/2 - i/2.
Therefore, the factored form using complex numbers is:
2(x - (-1/2 + i/2))(x - (-1/2 - i/2)) = 2(x + 1/2 - i/2)(x + 1/2 + i/2)
This can be further simplified, but it remains a factorization involving complex numbers, not real numbers.
Completing the Square
Another technique is completing the square. This method involves manipulating the quadratic expression to create a perfect square trinomial, which can then be factored easily. Let's try this method:
2x² + 2x + 1 = 0
Divide by 2:
x² + x + 1/2 = 0
To complete the square, we take half of the coefficient of x (which is 1), square it (1/4), and add and subtract it:
x² + x + 1/4 - 1/4 + 1/2 = 0
(x + 1/2)² + 1/4 = 0
(x + 1/2)² = -1/4
Taking the square root:
x + 1/2 = ±√(-1/4) = ±i/2
x = -1/2 ± i/2
This again confirms the complex roots, reinforcing the fact that the original quadratic cannot be factored using real numbers.
Why is Factoring Important? Applications of Quadratic Equations
The inability to factor 2x² + 2x + 1 using real numbers doesn't diminish the importance of quadratic factorization. Quadratic equations and their solutions have wide-ranging applications across numerous fields:
- Physics: Describing projectile motion, calculating the trajectory of objects under gravity.
- Engineering: Designing structures, analyzing stresses and strains in materials.
- Economics: Modeling supply and demand, optimizing production and pricing strategies.
- Computer Science: Developing algorithms, solving optimization problems.
- Mathematics: Solving various problems in calculus, geometry, and other advanced mathematical areas.
Frequently Asked Questions (FAQ)
-
Q: Can all quadratic expressions be factored? A: No, not all quadratic expressions can be factored using real numbers. As demonstrated with 2x² + 2x + 1, some quadratics have complex roots and therefore cannot be factored using only real numbers.
-
Q: What if I need to solve a quadratic equation that doesn't factor easily? A: The quadratic formula always provides a solution, even if the quadratic doesn't factor nicely. This formula gives the roots, whether they are real or complex.
-
Q: Is there any other way to factor this expression besides using complex numbers? A: No, there's no way to factor 2x² + 2x + 1 into real linear factors. The nature of its roots dictates this. Using complex numbers is the only way to achieve a complete factorization.
Conclusion: The Significance of Unfactorable Quadratics
While the inability to factor 2x² + 2x + 1 using real numbers might seem limiting, it highlights the rich and nuanced nature of quadratic expressions and their solutions. The appearance of complex roots opens doors to more advanced mathematical concepts and demonstrates that even seemingly simple expressions can lead to unexpected and fascinating results. Understanding the limitations of traditional factoring methods, alongside the power of the quadratic formula and the concept of the discriminant, provides a complete understanding of quadratic expressions and their applications in various fields. The exploration of this specific example serves as a valuable lesson in the broader context of algebra and mathematics.
Latest Posts
Latest Posts
-
Boric Acid Reaction With Water
Sep 12, 2025
-
Balance Na H2o Naoh H2
Sep 12, 2025
-
1 4 Equals How Many Sixteenths
Sep 12, 2025
-
I M The Most Beautiful Count
Sep 12, 2025
-
Simplify Square Root Of 39
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Factor 2x 2 1x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.