1/4 Equals How Many Sixteenths
thesills
Sep 12, 2025 · 6 min read
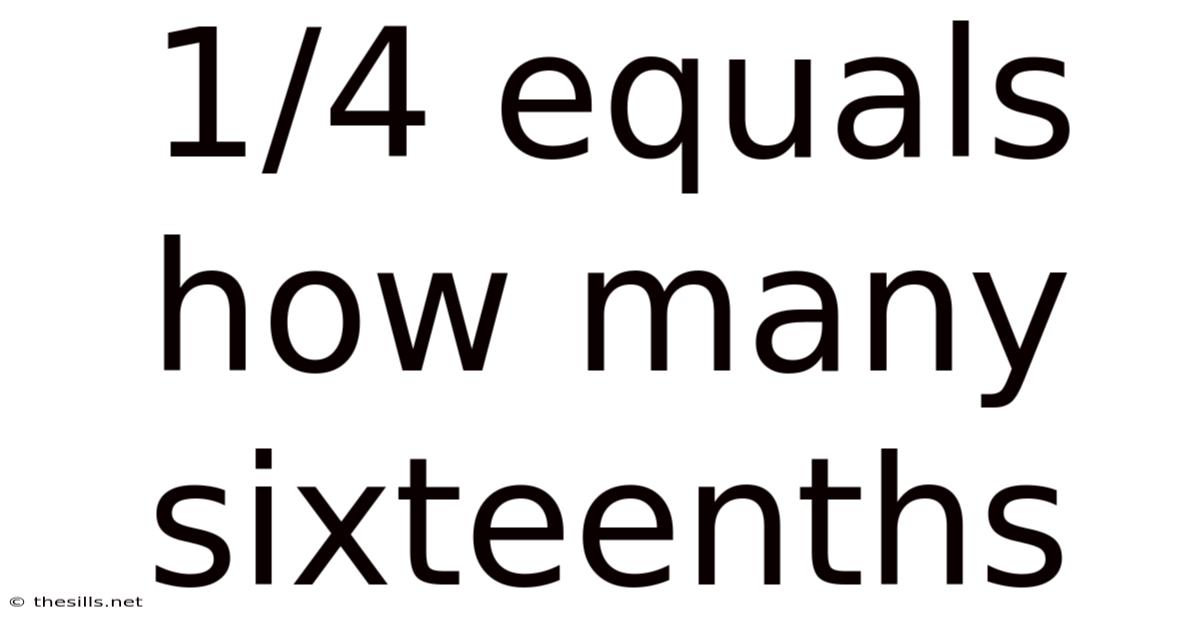
Table of Contents
1/4 Equals How Many Sixteenths? Understanding Fractions and Equivalents
This article explores the fundamental concept of equivalent fractions, focusing specifically on the question: how many sixteenths are equal to one-quarter (1/4)? We'll delve into the underlying mathematical principles, providing a clear and comprehensive understanding suitable for learners of all levels. We’ll cover various methods for solving this problem, including visual representations and step-by-step calculations, ensuring a strong grasp of the concept. By the end, you'll not only know the answer but also possess the tools to solve similar fractional equivalence problems independently.
Understanding Fractions: A Quick Recap
Before diving into the specifics of converting 1/4 to sixteenths, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number, indicating the number of parts we're considering.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/4, the numerator (1) represents one part, and the denominator (4) means the whole is divided into four equal parts.
Visualizing 1/4 and Sixteenths
A visual approach can greatly aid comprehension. Imagine a square divided into four equal parts. Shading one of these parts represents 1/4.
Now, imagine the same square, but this time divided into sixteen equal parts. How many of these sixteen smaller parts would be equivalent to the single shaded part representing 1/4? If you were to carefully count, you would find that four of the sixteenths equal one-quarter.
Method 1: Finding Equivalent Fractions through Multiplication
The most common method for converting fractions involves finding an equivalent fraction by multiplying both the numerator and the denominator by the same number. This doesn't change the value of the fraction; it simply represents the same proportion using different numbers.
To convert 1/4 to sixteenths, we need to find a number that, when multiplied by the denominator 4, results in 16. That number is 4 (because 4 x 4 = 16).
Therefore, we multiply both the numerator and the denominator of 1/4 by 4:
(1 x 4) / (4 x 4) = 4/16
This shows that 1/4 is equal to 4/16.
Method 2: Using Division to Simplify Fractions
Conversely, we can start with a larger fraction and simplify it to find an equivalent fraction. Let’s say we start with 4/16. To simplify, we find the greatest common divisor (GCD) of both the numerator and the denominator. The GCD of 4 and 16 is 4. Dividing both the numerator and the denominator by 4 gives:
(4 ÷ 4) / (16 ÷ 4) = 1/4
This demonstrates that 4/16 simplifies to 1/4, confirming our previous finding.
Method 3: Understanding the Relationship Between Fractions and Decimals
Converting fractions to decimals can also help visualize the equivalence. 1/4 as a decimal is 0.25. To express this as sixteenths, we can divide 0.25 by (1/16), which is equivalent to multiplying 0.25 by 16:
0.25 x 16 = 4
Again, this confirms that 1/4 is equal to 4/16.
The Importance of Equivalent Fractions in Mathematics
Understanding equivalent fractions is a cornerstone of many mathematical concepts. It's crucial for:
- Adding and subtracting fractions: Before you can add or subtract fractions, they must have a common denominator. Finding equivalent fractions allows you to achieve this.
- Simplifying fractions: Reducing fractions to their simplest form improves clarity and makes calculations easier.
- Solving equations: Many algebraic equations involve fractions, and understanding equivalent fractions is essential for solving them.
- Working with ratios and proportions: Ratios and proportions are often expressed as fractions, and finding equivalent fractions is necessary for comparing and manipulating them.
- Understanding percentages: Percentages are essentially fractions with a denominator of 100. Understanding equivalent fractions allows for easy conversion between fractions and percentages.
Expanding the Concept: Other Equivalents of 1/4
While we focused on sixteenths, 1/4 can be expressed as many equivalent fractions. For instance:
- Eighths: 1/4 = 2/8 (multiply numerator and denominator by 2)
- Thirty-seconds: 1/4 = 8/32 (multiply numerator and denominator by 8)
- Hundredths: 1/4 = 25/100 (multiply numerator and denominator by 25)
The possibilities are endless, as long as you multiply both the numerator and the denominator by the same number.
Practical Applications of Equivalent Fractions
Equivalent fractions are not just an abstract mathematical concept; they have numerous real-world applications. Consider these examples:
- Cooking and Baking: Recipes often require fractions of ingredients. Understanding equivalent fractions allows you to adjust recipes based on the quantities available. If a recipe calls for 1/4 cup of sugar, and you only have measuring spoons, you can easily convert it to 4/16 cup (which is easier to measure using a 1/16 cup measuring spoon).
- Construction and Engineering: Precise measurements are vital in construction and engineering. Converting fractions to equivalent fractions with smaller denominators often makes accurate measurements easier and more practical.
- Finance and Budgeting: Understanding fractions is important for managing personal finances and understanding proportions of income and expenditure. Converting fractions helps with calculations involving budgeting and saving.
- Data Analysis and Statistics: Fractions are frequently used in data analysis to represent proportions and percentages. Understanding equivalent fractions simplifies the interpretation and comparison of different data sets.
Frequently Asked Questions (FAQ)
Q: Why is it important to multiply both the numerator and the denominator by the same number when finding equivalent fractions?
A: Multiplying both the numerator and the denominator by the same number maintains the ratio of the fraction. It's like scaling a map; you enlarge or reduce the size, but the relative positions remain the same. If you only multiplied the numerator or the denominator, you would change the value of the fraction.
Q: Can I divide the numerator and denominator by the same number to find an equivalent fraction?
A: Yes! This is the process of simplifying a fraction. You find the greatest common divisor (GCD) of the numerator and the denominator and divide both by the GCD. This gives you the simplest form of the fraction.
Q: What if I have a fraction with a very large denominator? How do I find an equivalent fraction with a smaller denominator?
A: Find the greatest common divisor (GCD) of the numerator and denominator. Divide both by the GCD. This will simplify the fraction to its lowest terms. If you need a specific denominator, you may need to find the least common multiple (LCM) and adjust accordingly.
Q: Is there a limit to the number of equivalent fractions that can be found for a given fraction?
A: No, there is no limit. You can always find another equivalent fraction by multiplying the numerator and the denominator by any non-zero number.
Conclusion: Mastering the Art of Fractional Equivalence
Understanding equivalent fractions is a vital skill in mathematics and has far-reaching practical applications. We've explored various methods for determining that 1/4 equals 4/16, solidifying this fundamental concept through visual representations, step-by-step calculations, and real-world examples. Remember, the key to finding equivalent fractions is to multiply or divide both the numerator and the denominator by the same non-zero number. By mastering this skill, you'll build a strong foundation for tackling more complex mathematical problems and applying this knowledge to various aspects of your life.
Latest Posts
Latest Posts
-
Type Of Bonding In Hcl
Sep 12, 2025
-
X 3 3x 1 0
Sep 12, 2025
-
Fe2o3 Co Fe Co2 Balanced
Sep 12, 2025
-
What Is 1 20 Slope
Sep 12, 2025
-
Are Plant Unicellular Or Multicellular
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Equals How Many Sixteenths . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.