X 3 3x 1 0
thesills
Sep 12, 2025 · 6 min read
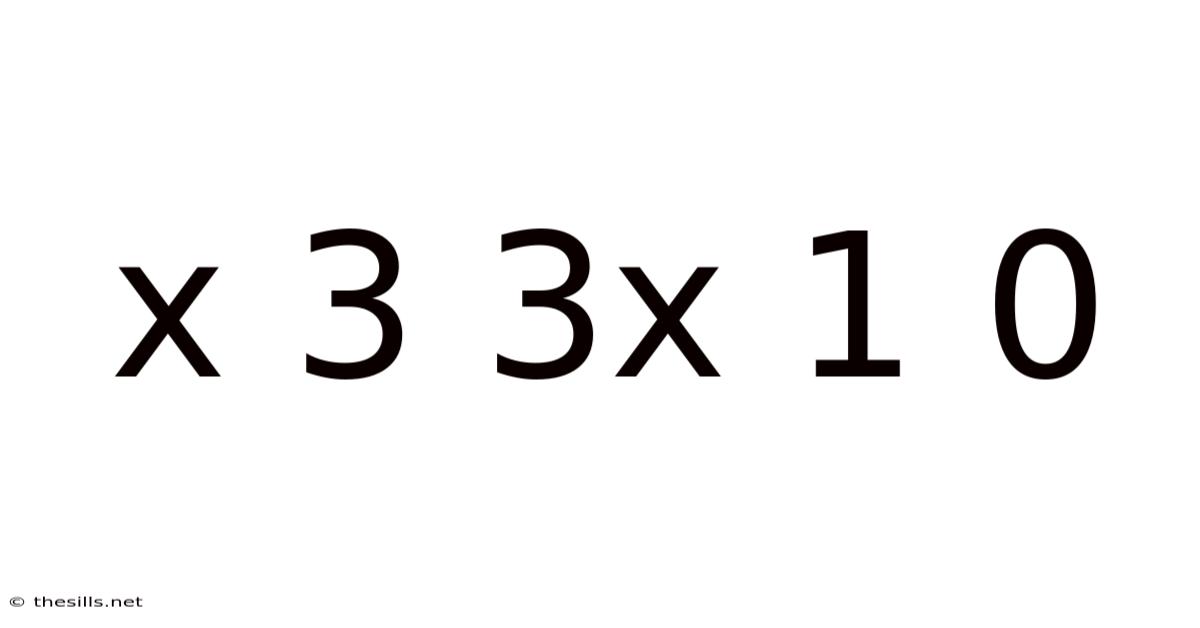
Table of Contents
Decoding the Mystery: Exploring the Mathematical Significance of "x 3 3x 1 0"
This article delves into the mathematical expression "x 3 3x 1 0," exploring its meaning, solutions, and broader implications within algebra and beyond. We'll unpack its structure, demonstrate how to solve it using various methods, and discuss the significance of finding its roots. This seemingly simple equation holds a wealth of mathematical concepts that are fundamental to understanding more complex problems. Whether you're a high school student grappling with algebra or a curious individual seeking to expand your mathematical knowledge, this comprehensive guide will provide a clear and insightful understanding.
Understanding the Equation: A Breakdown
The expression "x 3 3x 1 0" represents a cubic equation. A cubic equation is a polynomial equation of degree three, meaning the highest power of the variable x is 3. The general form of a cubic equation is ax³ + bx² + cx + d = 0, where a, b, c, and d are constants, and 'a' is not equal to zero. In our specific case:
- a = 1: The coefficient of x³ is 1.
- b = 0: The coefficient of x² is 0.
- c = 3: The coefficient of x is 3.
- d = -1: The constant term is -1.
This seemingly simple change in coefficients significantly impacts the solutions and the methods used to find them. The absence of an x² term simplifies the equation somewhat, but the presence of the other terms necessitates a more sophisticated approach than simply factoring.
Methods for Solving Cubic Equations: A Comparative Analysis
Several methods exist for solving cubic equations, each with its own advantages and disadvantages. Let's explore some of the most common approaches to solving "x³ + 3x - 1 = 0."
1. The Rational Root Theorem
The Rational Root Theorem helps us identify potential rational roots (roots that are fractions). It states that any rational root of the polynomial equation must be of the form p/q, where p is a factor of the constant term (d) and q is a factor of the leading coefficient (a).
In our equation (x³ + 3x - 1 = 0), the constant term is -1 and the leading coefficient is 1. Therefore, the potential rational roots are ±1. Let's test these:
- If x = 1: 1³ + 3(1) - 1 = 3 ≠ 0
- If x = -1: (-1)³ + 3(-1) - 1 = -5 ≠ 0
Since neither ±1 are roots, this method doesn't directly provide a solution. This indicates that the roots are likely irrational or complex.
2. Numerical Methods: Approximating the Solutions
When analytical methods fail to provide exact solutions, numerical methods offer approximations. These methods iteratively refine an initial guess to approach the true root. Popular numerical methods include:
-
Newton-Raphson Method: This iterative method uses the derivative of the function to refine the approximation. The formula is: x_(n+1) = x_n - f(x_n) / f'(x_n), where x_n is the current approximation, f(x_n) is the function value at x_n, and f'(x_n) is the derivative at x_n.
-
Bisection Method: This method repeatedly halves an interval known to contain a root. It's simpler than Newton-Raphson but converges more slowly.
These methods require an initial guess and involve iterative calculations. While they don't yield exact solutions in symbolic form, they provide accurate numerical approximations to the roots. Applying these methods to our equation would reveal that there is one real root and two complex conjugate roots.
3. Cardano's Method: A Classical Approach
Cardano's method is a general algebraic method for solving cubic equations. It involves a series of substitutions and manipulations to reduce the cubic equation to a simpler form that can be solved. However, this method can be quite complex and involves dealing with complex numbers, even when the final solutions are real numbers. Applying Cardano's method to x³ + 3x - 1 = 0 involves the following steps:
-
Depressing the Cubic: A substitution is used to eliminate the quadratic term (x²). This results in a depressed cubic equation of the form y³ + py + q = 0.
-
Solving the Depressed Cubic: Cardano's formula provides a solution for y in terms of p and q. This formula involves cube roots and complex numbers, even if the final solution for y is a real number.
-
Back Substitution: Once the value(s) of y are found, they are substituted back into the original substitution equation to find the value(s) of x.
The application of Cardano's method to our equation is algebraically intensive and will be omitted here due to space constraints, but it would reveal the exact values (both real and complex) of x that satisfy the equation. While powerful, it's often computationally demanding and is best left to symbolic computation software.
The Significance of the Roots and their Implications
The roots of the equation x³ + 3x - 1 = 0 hold significant mathematical importance. Finding these roots allows us to:
-
Understand the function's behavior: The roots represent the points where the function y = x³ + 3x - 1 intersects the x-axis. Knowing these points allows us to sketch the graph of the function accurately.
-
Solve related problems: This equation might represent a physical model in various applications, such as engineering or physics. Solving the equation is crucial in understanding and predicting the system's behavior.
-
Further mathematical explorations: The equation serves as a basis for exploring more advanced concepts in algebra, such as field extensions, Galois theory, and the study of polynomial equations.
The real root of the equation is approximately 0.322, while the other two roots are complex conjugates. The presence of complex roots is not uncommon in cubic equations and often indicates phenomena not directly observable in the real world but crucial for a complete mathematical description.
Frequently Asked Questions (FAQ)
Q1: Are there other methods to solve cubic equations?
A1: Yes, several other methods exist, including graphical methods, iterative numerical techniques like the secant method and the regula falsi method, and advanced techniques from numerical analysis. The choice of method depends on the specific equation and the desired accuracy of the solution.
Q2: Why is finding the roots of this equation important?
A2: Finding the roots allows us to completely characterize the behavior of the cubic function. The roots are critical points on the graph, and they provide valuable insight into the function's properties and potential applications in diverse fields.
Q3: Can all cubic equations be solved algebraically?
A3: While there is a general algebraic solution (like Cardano's method), it can become extremely cumbersome for certain cubic equations. Numerical methods often provide a more practical approach for complex or high-degree polynomials.
Q4: What does it mean when a cubic equation has complex roots?
A4: Complex roots often appear in mathematical models of physical systems and represent aspects that are not immediately observable in the real world. While the imaginary part might not have direct physical significance, the presence of complex roots indicates the full mathematical solution requires this extension beyond real numbers.
Conclusion: Beyond the Equation
The seemingly simple equation, x³ + 3x - 1 = 0, opens a door to a fascinating world of mathematical concepts and techniques. Solving this equation involves a blend of algebraic manipulation, numerical approximation, and a deep understanding of polynomial behavior. While the methods presented here provide a comprehensive overview, the true beauty lies in the interconnectedness of these mathematical tools and their applications in diverse fields, underscoring the fundamental importance of understanding polynomial equations, especially cubic equations, in our pursuit of mathematical knowledge. The exploration extends beyond just finding a solution; it's about comprehending the underlying mathematical principles and appreciating the elegance and power of mathematical methods.
Latest Posts
Latest Posts
-
Difference Between Microscope And Telescope
Sep 12, 2025
-
Copper Wiring Vs Silver Wiring
Sep 12, 2025
-
Sentence Using The Word Constitution
Sep 12, 2025
-
Indefinite Shape And Indefinite Volume
Sep 12, 2025
-
What Is 2x Times 3x
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about X 3 3x 1 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.