What Is 2x Times 3x
thesills
Sep 12, 2025 · 5 min read
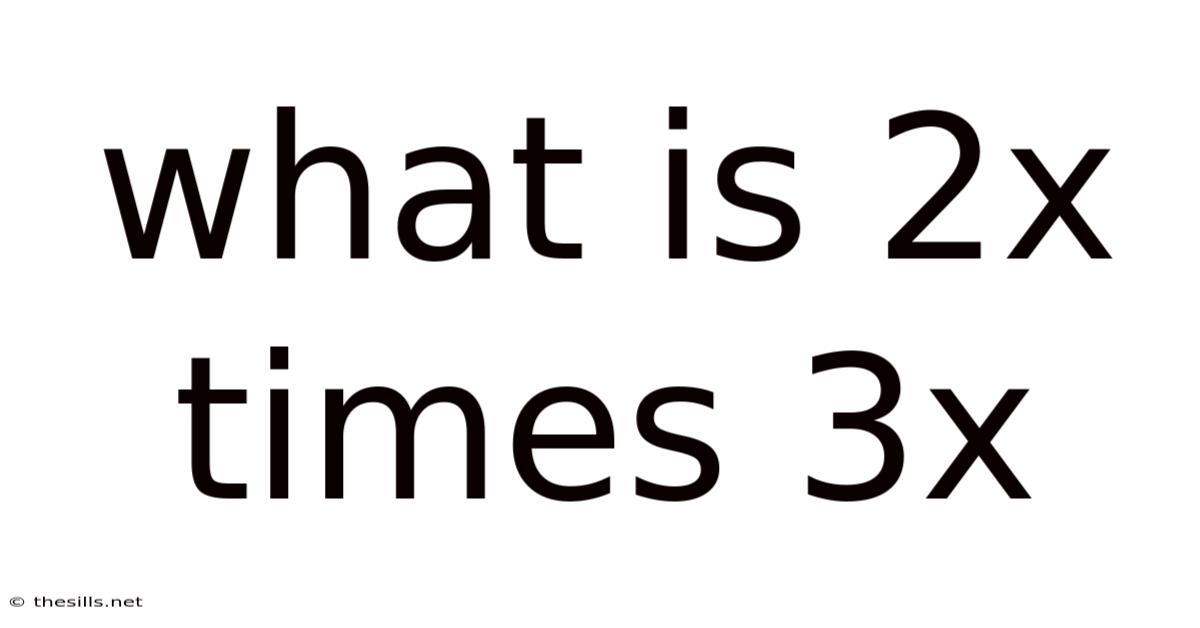
Table of Contents
What is 2x times 3x? Unlocking the Power of Algebraic Multiplication
This article will delve into the seemingly simple yet fundamentally important question: what is 2x times 3x? While the answer might appear straightforward at first glance, understanding the underlying principles of algebraic multiplication is crucial for success in mathematics, particularly algebra and beyond. We'll explore this calculation step-by-step, explaining the rules and providing a deeper understanding of the concepts involved, including the use of coefficients and variables, and extending this understanding to more complex scenarios.
Understanding the Fundamentals: Coefficients and Variables
Before we tackle the multiplication of 2x and 3x, let's break down the components of these algebraic expressions. In algebra, we frequently encounter expressions containing two main elements:
-
Coefficients: These are the numerical values that precede a variable. In 2x, the coefficient is 2. Similarly, in 3x, the coefficient is 3. Coefficients represent the quantity or multiplier of the variable.
-
Variables: These are usually represented by letters (often x, y, or z) and stand for unknown or unspecified values. In both 2x and 3x, 'x' is the variable. The variable represents a quantity that can change or vary.
Multiplying 2x and 3x: A Step-by-Step Guide
Now, let's address the main question: what is 2x times 3x? This involves multiplying two algebraic terms together. The process can be broken down into these simple steps:
-
Multiply the Coefficients: First, multiply the coefficients of the two terms together. In this case, we multiply 2 and 3: 2 * 3 = 6
-
Multiply the Variables: Next, multiply the variables together. Since both terms have the variable 'x', we multiply x by x: x * x = x²
-
Combine the Results: Combine the result of the coefficient multiplication and the variable multiplication. This gives us the final answer: 6x²
Therefore, 2x times 3x equals 6x².
The Power of Exponents: Understanding x²
The result, 6x², includes the term x². This term uses exponents, a crucial concept in algebra. An exponent indicates how many times a base number is multiplied by itself. In x², the base is 'x', and the exponent is 2. This means x² is equivalent to x * x. Understanding exponents is crucial for solving many algebraic problems and equations.
Expanding the Concept: Multiplying More Complex Algebraic Expressions
The principles discussed above can be extended to more complex expressions. Let's consider a few examples:
-
Example 1: (2x)(5y): Here, we have different variables. We multiply the coefficients (2 * 5 = 10) and then multiply the variables (x * y = xy). The result is 10xy.
-
Example 2: (4x²)(3x): This involves multiplying terms with exponents. Multiply the coefficients (4 * 3 = 12). Then, multiply the variables (x² * x = x³). Remember that when multiplying variables with exponents, you add the exponents (2 + 1 = 3). The result is 12x³.
-
Example 3: (2x + 3)(x - 1): This is an example of multiplying binomials (expressions with two terms). This requires the use of the distributive property or the FOIL method (First, Outer, Inner, Last).
- FOIL Method:
- First: (2x)(x) = 2x²
- Outer: (2x)(-1) = -2x
- Inner: (3)(x) = 3x
- Last: (3)(-1) = -3
- Combine Like Terms: 2x² - 2x + 3x - 3 = 2x² + x - 3
Therefore, (2x + 3)(x - 1) = 2x² + x - 3.
- FOIL Method:
These examples demonstrate the adaptability of the fundamental principles of algebraic multiplication to more intricate scenarios. Mastering the basic concepts of multiplying coefficients and variables is the foundation for tackling more advanced algebraic problems.
The Importance of Order of Operations (PEMDAS/BODMAS)
In more complex algebraic expressions, remember the order of operations. PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) dictates the sequence of operations. Multiplication and division are performed before addition and subtraction. Always follow the order of operations to arrive at the correct result.
Real-World Applications of Algebraic Multiplication
Algebraic multiplication isn't just a theoretical concept; it has numerous real-world applications across various fields:
-
Physics: Calculating area, volume, velocity, and acceleration often involves algebraic multiplication.
-
Engineering: Designing structures, circuits, and systems relies heavily on algebraic manipulations, including multiplication.
-
Finance: Calculating compound interest, determining investment returns, and analyzing financial models all necessitate algebraic skills.
-
Computer Science: Programming and algorithm development often involve algebraic operations to solve complex computational problems.
Understanding and mastering algebraic multiplication is crucial for success in these and many other fields.
Frequently Asked Questions (FAQ)
Q: What if the variables are different?
A: If the variables are different (e.g., 2x * 3y), you multiply the coefficients as usual (2 * 3 = 6), but the variables remain separate (x * y = xy). The result is 6xy.
Q: What if one term has a negative coefficient?
A: Treat the negative sign as part of the coefficient. For example, (-2x)(3x) = -6x². Remember that a negative times a positive is negative.
Q: What happens if the expression involves more than two terms?
A: You apply the distributive property. Multiply each term in the first expression by each term in the second expression and then combine like terms.
Q: Can I use a calculator for this type of multiplication?
A: While a standard calculator might struggle with algebraic expressions directly, scientific calculators or computer algebra systems can handle these calculations. However, understanding the manual process is crucial for deeper comprehension and problem-solving.
Conclusion: Mastering the Fundamentals of Algebraic Multiplication
Understanding how to multiply algebraic expressions, particularly the basic multiplication of terms like 2x and 3x, is a fundamental building block in mathematics. By grasping the concepts of coefficients, variables, exponents, and the order of operations, you build a strong foundation for tackling more complex algebraic problems and applying these principles to various real-world situations. Remember, consistent practice and a clear understanding of the underlying principles are key to mastering algebraic multiplication. Keep practicing and soon you'll be confidently solving even the most challenging algebraic expressions.
Latest Posts
Latest Posts
-
Rotational Constant Of Diatomic Molecules
Sep 12, 2025
-
Acetic Acid And Ammonia Reaction
Sep 12, 2025
-
Integral X 2e X 2
Sep 12, 2025
-
Aroy D Coconut Milk Ingredients
Sep 12, 2025
-
Why Is Replication Called Semi Conservative
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 2x Times 3x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.