Integral X 2e X 2
thesills
Sep 12, 2025 · 6 min read
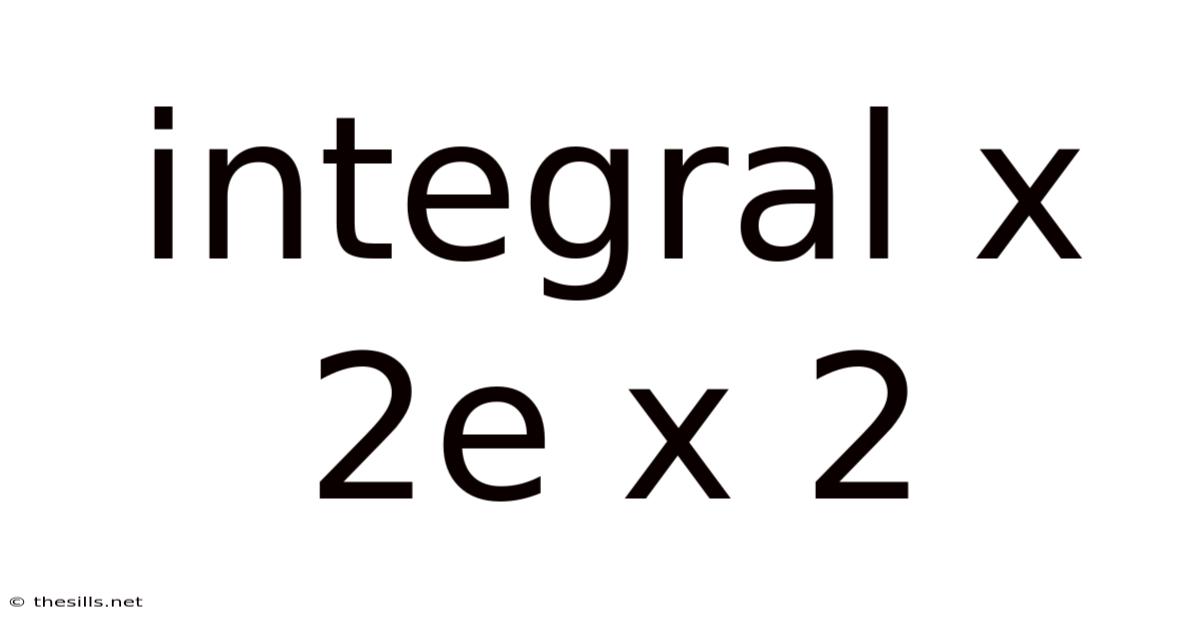
Table of Contents
Solving the Integral of x²e^(x²)
This article delves into the intricacies of solving the definite integral ∫x²e^(x²) dx. While this integral doesn't possess a solution expressible in terms of elementary functions (like polynomials, exponentials, logarithms, trigonometric functions, and their inverses), understanding the approaches to solving it provides valuable insights into advanced calculus techniques. We'll explore various methods, highlighting their limitations and offering a deeper appreciation for the nature of integration. This guide is perfect for students studying calculus, particularly those encountering more challenging integration problems.
Introduction: Why This Integral is Challenging
The integral ∫x²e^(x²) dx presents a significant challenge because there's no straightforward antiderivative. Unlike simpler integrals, such as ∫xe^x dx (which can be solved using integration by parts), this integral resists elementary techniques. The presence of both a polynomial (x²) and an exponential function (e^(x²)) intertwined makes direct integration difficult. This necessitates exploring alternative strategies and understanding the limitations of standard calculus methods.
Attempting Integration by Parts
A common approach to tackling integrals involving products of functions is integration by parts. The formula is:
∫u dv = uv - ∫v du
Let's attempt to apply this method. We could choose:
- u = x² => du = 2x dx
- dv = e^(x²) dx => v = ?
The problem arises in finding 'v'. There isn't an elementary antiderivative for e^(x²) dx. This highlights the core difficulty: the exponential function with a quadratic exponent lacks a simple antiderivative within the realm of elementary functions.
Exploring Other Techniques
Since integration by parts fails, we might explore other techniques, such as:
- Substitution: Substitution typically involves identifying a suitable substitution (u) to simplify the integral. However, no obvious substitution simplifies the given integral sufficiently.
- Partial Fraction Decomposition: This method applies to rational functions (ratios of polynomials). The given integral involves an exponential function and therefore doesn't lend itself to this technique.
- Trigonometric Substitution: This technique is valuable for integrals involving square roots of quadratic expressions. This integral does not contain such expressions.
The limitations of these standard techniques underscore the need for more advanced approaches or accepting the integral in its current form (without an elementary antiderivative).
Advanced Approaches and Special Functions
To evaluate definite integrals of this type, we must resort to numerical methods or introduce special functions beyond the scope of elementary calculus.
-
Numerical Integration Techniques: Methods like the Trapezoidal Rule, Simpson's Rule, or Gaussian Quadrature can approximate the definite integral over a specified interval. These methods rely on numerical computation rather than finding an analytical solution. The accuracy of the approximation depends on the chosen method and the number of intervals used.
-
Error Function (erf) and Related Functions: The integral ∫e^(-x²) dx is closely related to the error function, denoted as erf(x). While not directly applicable to our integral, understanding the error function illuminates the challenges associated with integrals involving Gaussian functions. The error function itself is a special function that doesn't have an elementary antiderivative expression.
-
Series Expansions: We can express e^(x²) using its Maclaurin series expansion:
e^(x²) = 1 + x² + (x²)²/2! + (x²)³/3! + ...
Substituting this into the integral, we obtain:
∫x²e^(x²) dx = ∫x²(1 + x² + (x²)²/2! + (x²)³/3! + ...) dx
This simplifies to a series of power integrals that are solvable. However, the resulting series representation is an infinite series, not a closed-form solution using elementary functions.
Numerical Integration: A Practical Approach
Let's illustrate a numerical approach using the Trapezoidal Rule. Suppose we want to approximate the definite integral:
∫₀¹ x²e^(x²) dx
The Trapezoidal Rule approximates the integral as:
∫ₐᵇ f(x) dx ≈ (b-a)/2n * [f(x₀) + 2f(x₁) + 2f(x₂) + ... + 2f(xₙ₋₁) + f(xₙ)]
where:
- a = 0
- b = 1
- n is the number of intervals (let's choose n = 10 for simplicity)
- xᵢ = a + i(b-a)/n
Applying the Trapezoidal Rule with n=10 will yield an approximation of the definite integral. However, it's crucial to understand this is only an approximation, not the exact analytical solution. Higher values of 'n' will generally result in a more accurate approximation.
The Importance of Understanding Limitations
The integral ∫x²e^(x²) dx serves as a valuable lesson. It demonstrates that not all integrals possess solutions expressible in terms of elementary functions. While standard integration techniques might fail, advanced numerical methods or series expansions can provide approximate or series solutions, respectively. Understanding these limitations is essential for developing a comprehensive understanding of calculus and its applications.
Frequently Asked Questions (FAQ)
Q1: Can this integral be solved using any standard integration techniques?
A1: No, standard techniques like integration by parts, substitution, partial fraction decomposition, and trigonometric substitution are not sufficient to find an elementary antiderivative for this integral.
Q2: What are some numerical methods for approximating the definite integral?
A2: The Trapezoidal Rule, Simpson's Rule, and Gaussian Quadrature are examples of numerical integration techniques that can be used to approximate the definite integral over a specified interval.
Q3: Does this integral have a closed-form solution?
A3: No, it does not have a closed-form solution expressible using elementary functions. The solution would involve infinite series or special functions.
Q4: Why is this integral considered challenging?
A4: The combination of a polynomial (x²) and an exponential function (e^(x²)) with a quadratic exponent creates an integral that resists standard integration techniques. The exponential term with the quadratic exponent lacks a simple antiderivative within the realm of elementary functions.
Q5: What is the significance of the error function in relation to this problem?
A5: The error function (erf(x)) is closely related to integrals involving Gaussian functions (e^(-x²)). While not directly applicable to solving ∫x²e^(x²) dx, it highlights the challenges associated with integrals of similar structure that require special functions for a solution.
Conclusion: A Deeper Understanding of Integration
The journey of attempting to solve the integral ∫x²e^(x²) dx reveals the rich landscape of calculus. While standard integration techniques fall short, this integral illustrates the importance of numerical methods and the existence of special functions beyond the realm of elementary functions. This exploration reinforces the concept that not all integrals yield neat, closed-form solutions, and alternative approaches are necessary to gain insights and approximate solutions. Understanding this limitation is a crucial step in mastering more advanced calculus concepts. The integral serves as an excellent example showcasing the interplay between analytical and numerical approaches in solving complex mathematical problems. It underscores the power and limitations of different mathematical tools, ultimately leading to a more complete and nuanced understanding of integration.
Latest Posts
Latest Posts
-
Conditions For Total Internal Reflection
Sep 12, 2025
-
Difference Between Orbit And Orbital
Sep 12, 2025
-
Bond Order Of O2 2
Sep 12, 2025
-
71 250 As A Decimal
Sep 12, 2025
-
Difference Between Hormone And Enzyme
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Integral X 2e X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.