Derivative Of Sec X Tanx
thesills
Sep 18, 2025 · 5 min read
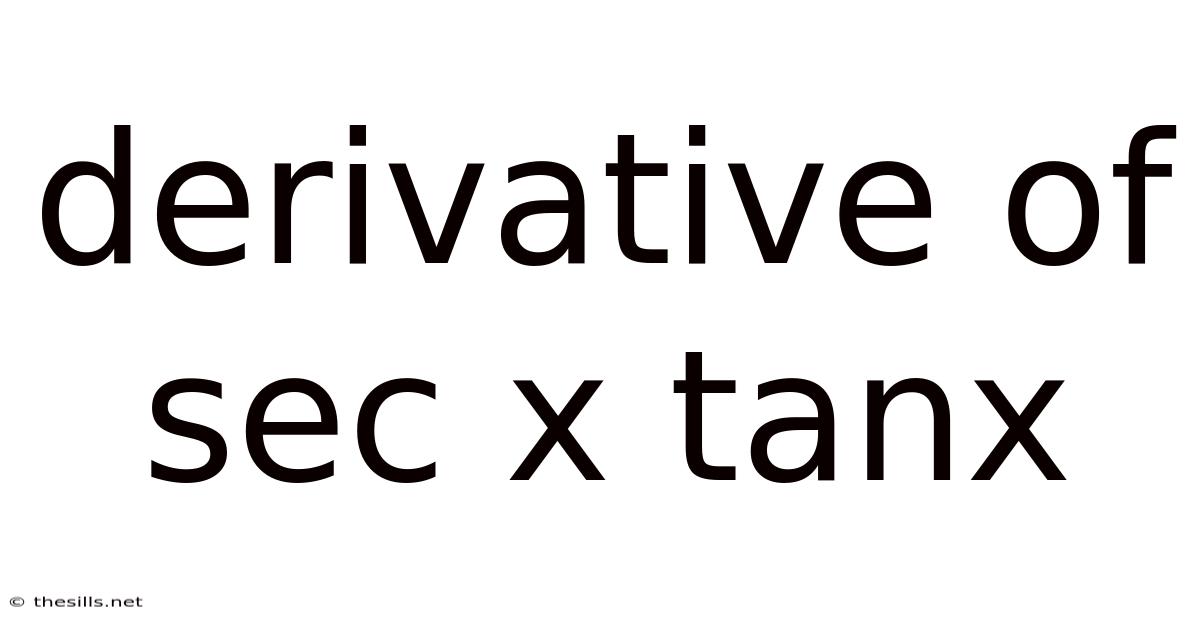
Table of Contents
Delving Deep into the Derivative of sec x tan x: A Comprehensive Guide
Finding the derivative of sec x tan x might seem daunting at first, but with a systematic approach and a solid understanding of trigonometric functions and differentiation rules, it becomes surprisingly straightforward. This comprehensive guide will walk you through the process step-by-step, explaining the underlying principles and providing you with a deeper understanding of the topic. We'll cover various methods, explore the underlying mathematical concepts, and address frequently asked questions to ensure a complete grasp of this important calculus concept.
Introduction: Understanding the Building Blocks
Before we tackle the derivative of sec x tan x, let's refresh our understanding of the fundamental trigonometric functions and their derivatives. Remember that:
- sec x = 1/cos x (The secant of x is the reciprocal of the cosine of x)
- tan x = sin x / cos x (The tangent of x is the ratio of the sine of x to the cosine of x)
Knowing these definitions is crucial because we'll be using them extensively in our derivations. Furthermore, we need to be familiar with the basic derivative rules, including the product rule, quotient rule, and the derivatives of common trigonometric functions:
- d/dx (sin x) = cos x
- d/dx (cos x) = -sin x
Method 1: Applying the Product Rule
The most straightforward approach to finding the derivative of sec x tan x involves the product rule. The product rule states that the derivative of a product of two functions, u(x) and v(x), is given by:
d/dx [u(x)v(x)] = u'(x)v(x) + u(x)v'(x)
In our case, u(x) = sec x and v(x) = tan x. Therefore, we need to find the derivatives of sec x and tan x individually.
- Derivative of sec x: Using the quotient rule on sec x = 1/cos x, we get:
d/dx (sec x) = d/dx (1/cos x) = [0 * cos x - 1 * (-sin x)] / (cos x)² = sin x / (cos x)² = sec x tan x
- Derivative of tan x: Using the quotient rule on tan x = sin x / cos x, we get:
d/dx (tan x) = d/dx (sin x / cos x) = [cos x * cos x - sin x * (-sin x)] / (cos x)² = (cos²x + sin²x) / (cos²x) = 1 / (cos²x) = sec²x
Now, let's apply the product rule:
d/dx (sec x tan x) = (d/dx (sec x)) * tan x + sec x * (d/dx (tan x))
Substituting the derivatives we found:
d/dx (sec x tan x) = (sec x tan x) * tan x + sec x * (sec²x) = sec x tan²x + sec³x
Therefore, the derivative of sec x tan x is sec x tan²x + sec³x.
Method 2: Rewriting in terms of Sine and Cosine
An alternative approach involves rewriting sec x tan x entirely in terms of sine and cosine before differentiating. This method might seem longer, but it reinforces the fundamental definitions and provides a deeper understanding of the manipulation involved.
Remember:
sec x tan x = (1/cos x) * (sin x / cos x) = sin x / cos²x
Now, we can use the quotient rule to differentiate:
d/dx (sin x / cos²x) = [(cos²x)(cos x) - (sin x)(2cos x)(-sin x)] / (cos²x)²
Simplifying:
= (cos³x + 2sin²x cos x) / cos⁴x = cos x (cos²x + 2sin²x) / cos⁴x = (cos²x + 2sin²x) / cos³x
Since cos²x = 1 - sin²x, we can rewrite:
= (1 - sin²x + 2sin²x) / cos³x = (1 + sin²x) / cos³x
We can further manipulate this expression to arrive at the same result as Method 1:
= (cos²x + sin²x + sin²x) / cos³x = (1 + sin²x) / cos³x = (1/cos³x) + (sin²x/cos³x) = sec³x + sec x tan²x
Again, we arrive at the derivative: sec x tan²x + sec³x.
Explanation of the Result: A Deeper Dive
The derivative we obtained, sec x tan²x + sec³x, might seem complex at first glance. However, it's a perfectly valid and simplified expression derived from the fundamental rules of calculus and trigonometry. This derivative represents the instantaneous rate of change of the function sec x tan x at any given point x. Understanding this rate of change is crucial in various applications of calculus, particularly in physics and engineering where trigonometric functions often model oscillatory or periodic phenomena. The presence of both sec x and tan x (and their powers) in the derivative is expected, given that these are the building blocks of the original function.
Frequently Asked Questions (FAQ)
-
Q: Can I simplify the derivative further? A: While the expression sec x tan²x + sec³x is already simplified, you could factor out a sec x, resulting in sec x (tan²x + sec²x). This factored form might be useful in certain applications.
-
Q: What are some practical applications of this derivative? A: The derivative finds application in problems involving related rates, optimization, and the study of curves defined by trigonometric functions. For example, it could be used to find the rate of change of an angle in a rotating system or to determine the maximum or minimum values of a function involving sec x tan x.
-
Q: Are there other methods to find this derivative? A: While the product rule and rewriting using sine and cosine are the most direct methods, more advanced techniques like logarithmic differentiation could also be used. However, for a clear understanding of fundamental calculus principles, the methods described above are the most pedagogically effective.
-
Q: Why is it important to understand the underlying trigonometric identities? A: A strong understanding of trigonometric identities is crucial for simplifying expressions and manipulating equations, facilitating the derivation process. Without a good grasp of these identities, the simplification steps can become significantly more complex and error-prone.
Conclusion: Mastering the Derivative of sec x tan x
Finding the derivative of sec x tan x is a valuable exercise that strengthens your understanding of trigonometric functions, differentiation rules (specifically the product rule and quotient rule), and algebraic manipulation. By mastering this concept, you build a strong foundation for tackling more complex calculus problems involving trigonometric functions. Remember, practice is key. The more examples you work through, the more comfortable and confident you'll become in applying these techniques. The seemingly complex expression of the derivative, sec x tan²x + sec³x, ultimately represents a fundamental concept in calculus with practical applications in numerous fields. Understanding its derivation deepens your overall mathematical capabilities.
Latest Posts
Latest Posts
-
X Sin Pi X Integral
Sep 18, 2025
-
Reciprocal Of 1 1 2
Sep 18, 2025
-
Fathometer Is Used To Measure
Sep 18, 2025
-
Factor X 2 4x 1
Sep 18, 2025
-
2x 2 3x 4 0
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of Sec X Tanx . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.