2x 2 3x 4 0
thesills
Sep 18, 2025 · 6 min read
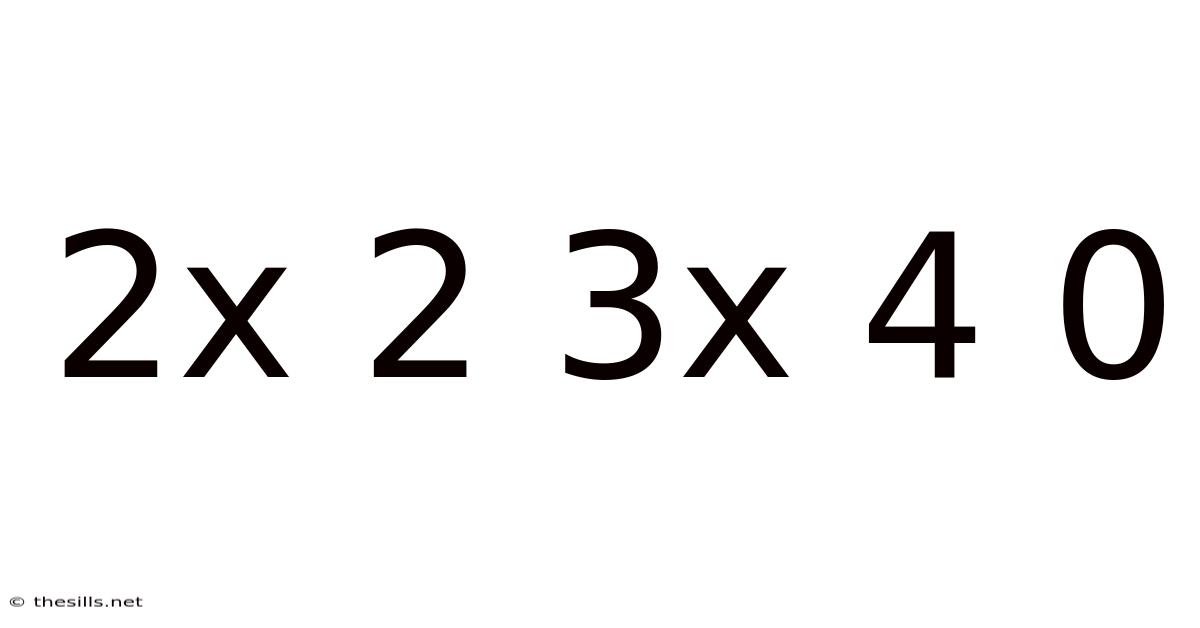
Table of Contents
Decoding the Mysterious Sequence: 2x2, 3x4, 0 – Unraveling Patterns and Possibilities
This article delves into the seemingly cryptic sequence "2x2, 3x4, 0," exploring its potential interpretations, underlying mathematical principles, and possible extensions. While the sequence itself is short and lacks immediate obvious patterns, we can employ various mathematical and logical approaches to analyze it, uncover hidden structures, and potentially generate a longer, more meaningful sequence. This investigation will explore different perspectives, from simple arithmetic operations to more complex considerations of sequences and series. Understanding this seemingly simple sequence requires creative problem-solving and a willingness to consider multiple possibilities.
Introduction: The Enigma of a Short Sequence
The sequence "2x2, 3x4, 0" presents a fascinating challenge. Its brevity makes it difficult to immediately identify a definitive pattern. However, this ambiguity is precisely what makes it an engaging problem. Instead of a single, definitive answer, we can explore multiple hypotheses, each revealing different facets of mathematical thinking and pattern recognition. The goal is not just to find a pattern, but to understand how we find patterns, and to develop a critical eye for analyzing numerical sequences. The "0" at the end is particularly intriguing, suggesting a potential shift or discontinuity in the pattern.
Exploring Potential Arithmetic Relationships
One approach to analyzing the sequence is to examine the arithmetic relationships between the elements.
-
Direct Calculation: The first two elements, 2x2 and 3x4, represent simple multiplications resulting in 4 and 12 respectively. The stark contrast between these values and the abrupt ending with "0" hints at a more complex pattern.
-
Difference Analysis: Examining the difference between consecutive elements, we find 12 - 4 = 8. However, this difference doesn't readily lead to a predictable next element. The significant jump from 12 to 0 disrupts any simple arithmetic progression.
-
Ratio Analysis: Calculating the ratio between consecutive elements yields 12/4 = 3. This ratio, while intriguing, again doesn't easily extend to incorporate the final 0.
The initial explorations using basic arithmetic operations are not sufficient to fully decipher this sequence. This leads us to investigate more sophisticated mathematical concepts.
Investigating Advanced Mathematical Concepts
The limitations of simple arithmetic operations encourage us to explore more complex mathematical patterns and relationships.
-
Sequences and Series: The sequence could be part of a larger sequence or series governed by a more intricate rule. Perhaps the sequence represents partial sums of another underlying sequence, or even a subsequence extracted from a larger pattern. This approach requires a significant leap of faith and demands a broader consideration of mathematical concepts. It's possible that the sequence is intentionally designed to be deceptive, with the apparent simplicity masking a more elaborate underlying structure.
-
Modular Arithmetic: Considering modular arithmetic, we might find a pattern that works within a specific modulus. However, without further data, finding a suitable modulus proving a consistent pattern is highly speculative. This line of inquiry demands additional numbers in the sequence to accurately identify a pattern within modular arithmetic.
-
Polynomial Functions: Another possible approach is to fit the sequence to a polynomial function. This would involve finding a polynomial equation that correctly produces the given values (4, 12, 0) for specific inputs. However, given only three data points, multiple polynomials could fit, making this approach less conclusive without further data. The low number of data points limits the ability to uniquely define the generating polynomial.
-
Geometric Progressions: Although the raw numbers themselves don't seem to form a direct geometric progression, a transformation of the numbers might. We can explore various transformations, like taking logarithms, square roots or other mathematical operations before testing for a geometric pattern. However, the presence of 0 severely complicates the search for geometric patterns.
-
Matrix Operations: While a stretch, we could hypothesize a matrix representation. Perhaps the sequence represents transformations within a matrix, where the 0 signifies a null or termination state. However, without any further context or additional data, this is purely speculative and provides no definitive answer.
Beyond Numerical Patterns: Exploring Alternative Interpretations
Given the limited information, we should consider interpretations beyond strictly numerical patterns.
-
Symbolic Representation: The 'x' symbol could have a meaning other than multiplication. It might denote a specific operation or relation, potentially leading to a non-arithmetic interpretation. The context or source of the sequence is crucial for deciphering such symbolic representation.
-
Code or Cipher: The sequence could be part of a code or cipher. The numbers might represent letters or symbols according to a specific encoding scheme. Without a key or additional information, cracking such a code is impossible.
-
Logical Sequence: The sequence might be related to a logical puzzle or game. For instance, the sequence could describe steps in a process or represent states in a system. This interpretation demands knowledge of the context where the sequence appears.
The Significance of "0"
The presence of "0" is particularly significant. It breaks any simple arithmetic or geometric progression, strongly indicating a change or termination point. It could represent:
-
A Reset: The 0 could symbolize a reset or a return to a starting point.
-
A Boundary Condition: It might indicate a boundary condition in a mathematical system or model.
-
A Termination Condition: It could signify the end of a process or the termination of a sequence.
Generating Hypotheses and Testing: A Scientific Approach
The lack of a clear pattern necessitates a more systematic and hypothesis-driven approach. We should generate several hypotheses about the possible meaning or structure of the sequence and then test each one.
-
Hypothesis 1: The sequence represents the results of a specific function applied to the numbers 2 and 3, and 0 serves as a termination condition.
-
Hypothesis 2: The sequence is a subsequence of a larger, more complex pattern, with 0 acting as a pivot point.
-
Hypothesis 3: The sequence encodes information using a specific encoding scheme.
-
Hypothesis 4: The sequence represents a pattern within a finite domain or a specific modular arithmetic system.
Each of these hypotheses would require further investigation and analysis to determine its validity. The process of testing these hypotheses may also suggest modifications or new avenues of exploration.
Conclusion: The Ongoing Search for Meaning
The sequence "2x2, 3x4, 0" remains an enigma, challenging our abilities to recognize patterns and apply diverse mathematical principles. The brevity of the sequence and the surprising inclusion of "0" significantly limit conclusive interpretations. While several potential explanations have been explored, without additional context or data, a definitive solution remains elusive. The exercise of attempting to unravel this short sequence, however, highlights the importance of creative problem-solving, a thorough understanding of various mathematical concepts, and the crucial role of context in deciphering patterns. The true beauty lies not just in finding an answer, but in the exploration of possibilities and the rigorous process of mathematical investigation. This sequence serves as a powerful reminder that even seemingly simple numerical arrangements can pose complex challenges, encouraging us to expand our mathematical toolkit and to think outside the box. The journey to understand this sequence mirrors the wider endeavor of mathematical discovery: a continual process of questioning, exploring, and refining our understanding.
Latest Posts
Latest Posts
-
Nonliving Things In The Rainforest
Sep 18, 2025
-
The Enzyme Substrate Complex Is
Sep 18, 2025
-
Mode Of Nutrition For Animalia
Sep 18, 2025
-
Can Marginal Product Be Negative
Sep 18, 2025
-
Food Web Of The Grassland
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 2x 2 3x 4 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.