Factor X 2 4x 1
thesills
Sep 18, 2025 · 6 min read
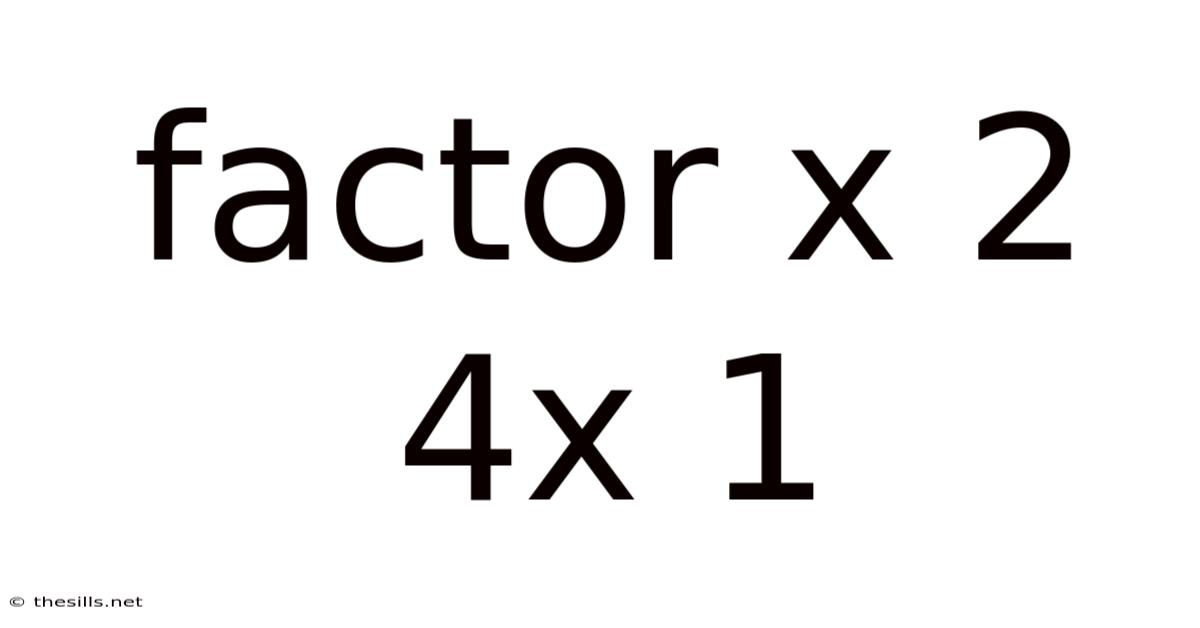
Table of Contents
Unraveling the Mysteries of the Quadratic Expression: x² + 4x + 1
Understanding quadratic expressions is fundamental to success in algebra and beyond. This comprehensive guide delves into the properties and solutions of the specific quadratic expression x² + 4x + 1, exploring its various forms, methods of solving it, and its applications in real-world scenarios. We'll move beyond simply finding the solutions and explore the deeper mathematical concepts involved.
Introduction: What Makes Quadratics Special?
Quadratic expressions, characterized by the presence of a variable raised to the power of two (x²), represent a significant step up from linear equations. Their solutions aren't always straightforward, requiring a deeper understanding of algebraic manipulation and sometimes the application of more advanced techniques. The specific expression x² + 4x + 1, while seemingly simple, provides a rich opportunity to explore these techniques and concepts. This article will guide you through understanding its properties, solving for its roots (or zeros), and appreciating its significance within a broader mathematical context.
Understanding the Components of x² + 4x + 1
Before we delve into solving the equation, let's break down its components:
-
x²: This term represents the quadratic term. It's the highest power of the variable x and gives the expression its characteristic parabolic shape when graphed.
-
4x: This is the linear term, a multiple of the variable x. It influences the position and slope of the parabola.
-
1: This is the constant term, an independent numerical value. It determines the y-intercept of the parabola (where the graph intersects the y-axis).
Understanding these individual components helps predict the overall behavior of the quadratic expression and its graphical representation.
Method 1: Solving using the Quadratic Formula
The quadratic formula is a powerful tool for solving any quadratic equation of the form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants. For our expression x² + 4x + 1, we have a = 1, b = 4, and c = 1. Plugging these values into the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
we get:
x = [-4 ± √(4² - 4 * 1 * 1)] / (2 * 1)
x = [-4 ± √(16 - 4)] / 2
x = [-4 ± √12] / 2
x = [-4 ± 2√3] / 2
Simplifying further:
x = -2 ± √3
Therefore, the two roots (or solutions) of the equation x² + 4x + 1 = 0 are:
- x = -2 + √3 ≈ -0.268
- x = -2 - √3 ≈ -3.732
These are the x-intercepts of the parabola represented by the equation.
Method 2: Completing the Square
Completing the square is another algebraic technique for solving quadratic equations. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. Let's apply this to x² + 4x + 1 = 0:
-
Move the constant term to the right side: x² + 4x = -1
-
Take half of the coefficient of the linear term (4), square it (4), and add it to both sides: x² + 4x + 4 = -1 + 4 x² + 4x + 4 = 3
-
Factor the perfect square trinomial: (x + 2)² = 3
-
Take the square root of both sides: x + 2 = ±√3
-
Solve for x: x = -2 ± √3
This yields the same solutions as the quadratic formula: x ≈ -0.268 and x ≈ -3.732.
Method 3: Graphical Representation
Graphing the quadratic equation provides a visual representation of its solutions. The x-intercepts of the parabola directly correspond to the roots of the equation. Plotting the equation y = x² + 4x + 1 will show a parabola intersecting the x-axis at approximately x = -0.268 and x = -3.732, confirming our earlier calculations. The vertex of the parabola can also be found using the formula x = -b/2a, which in this case is x = -2. Substituting this into the original equation gives the y-coordinate of the vertex as y = (-2)² + 4(-2) + 1 = -3. Therefore, the vertex of the parabola is (-2,-3).
This visual approach offers valuable intuition, illustrating the relationship between the equation's roots and its graphical representation.
The Discriminant: A Window into the Nature of Roots
The expression inside the square root in the quadratic formula (b² - 4ac) is called the discriminant. It provides valuable information about the nature of the roots:
- If b² - 4ac > 0: The equation has two distinct real roots (as in our case).
- If b² - 4ac = 0: The equation has one real root (a repeated root).
- If b² - 4ac < 0: The equation has two complex roots (involving imaginary numbers).
In our example, b² - 4ac = 16 - 4 = 12 > 0, indicating two distinct real roots.
Applications of Quadratic Equations in Real-World Scenarios
Quadratic equations are not merely abstract mathematical concepts; they have numerous practical applications:
-
Projectile Motion: The trajectory of a projectile (e.g., a ball thrown in the air) can be modeled using a quadratic equation, where the roots represent the points where the projectile hits the ground.
-
Area Calculations: Determining the dimensions of a rectangle with a given area and constraint on the sides often involves solving a quadratic equation.
-
Engineering and Physics: Many physical phenomena, such as the oscillation of a pendulum or the behavior of electrical circuits, can be described by quadratic equations.
-
Optimization Problems: Finding the maximum or minimum values of a function often requires solving quadratic equations. For instance, maximizing the area of a rectangular field given a fixed amount of fencing involves a quadratic equation.
Frequently Asked Questions (FAQ)
Q: Can I solve x² + 4x + 1 = 0 using factoring?
A: While the quadratic formula and completing the square are more direct methods for this specific equation, factoring is generally used when the quadratic expression can be easily factored into two binomial expressions. x² + 4x + 1 cannot be easily factored using integers.
Q: What does it mean if a quadratic equation has no real roots?
A: If the discriminant (b² - 4ac) is negative, the quadratic equation has no real roots. This means the parabola does not intersect the x-axis, and the roots are complex numbers involving the imaginary unit 'i' (√-1).
Q: Are there other methods to solve quadratic equations besides the ones mentioned?
A: Yes, numerical methods such as the Newton-Raphson method can be used to approximate the roots of quadratic equations, particularly when analytical methods are difficult to apply.
Conclusion: Mastering Quadratic Expressions
The seemingly simple quadratic expression x² + 4x + 1 offers a rich landscape for exploring fundamental algebraic concepts. Through various methods – the quadratic formula, completing the square, and graphical representation – we've uncovered its solutions and understood the underlying principles. This understanding isn't limited to theoretical mathematics; it extends to numerous real-world applications across diverse fields. By mastering quadratic equations, you equip yourself with a powerful tool for tackling complex problems and deepening your understanding of the world around us. Remember, the key to mastering mathematics lies in consistent practice and a willingness to explore different approaches to problem-solving. Keep exploring, keep questioning, and keep learning!
Latest Posts
Latest Posts
-
The Enzyme Substrate Complex Is
Sep 18, 2025
-
Mode Of Nutrition For Animalia
Sep 18, 2025
-
Can Marginal Product Be Negative
Sep 18, 2025
-
Food Web Of The Grassland
Sep 18, 2025
-
3 8 As A Percent
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 4x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.