A Number Decreased By 8
thesills
Sep 15, 2025 · 6 min read
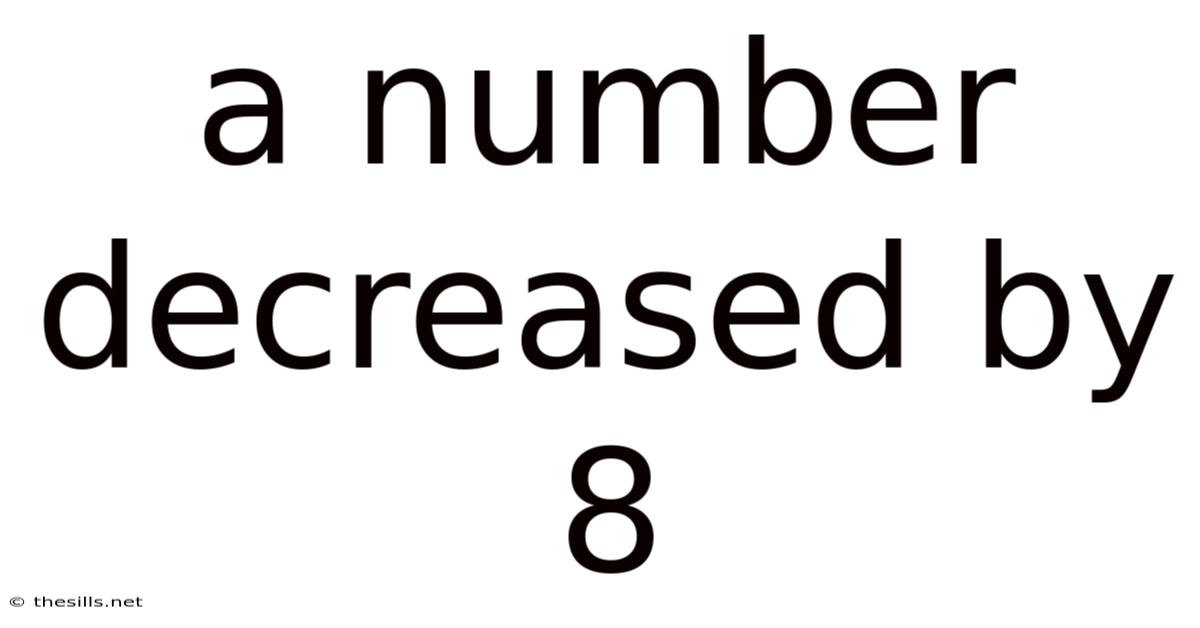
Table of Contents
Exploring the Mathematical Concept: A Number Decreased by 8
This article delves into the seemingly simple yet fundamentally important mathematical concept of "a number decreased by 8." While the phrase might appear basic, it forms the bedrock of algebraic thinking, equation solving, and a deeper understanding of arithmetic operations. We'll explore this concept from various angles, moving from basic arithmetic to more advanced applications, ensuring a comprehensive understanding for readers of all levels. Understanding this concept is crucial for building a strong foundation in mathematics and problem-solving.
Understanding the Fundamentals: Subtraction and Variables
At its core, "a number decreased by 8" describes a subtraction operation. We're taking away 8 from an unknown quantity, which we'll represent using a variable. In mathematics, a variable is a symbol, typically a letter like x, y, or n, that represents an unknown number or a quantity that can change.
Therefore, "a number decreased by 8" can be mathematically expressed as:
x - 8
where x represents the unknown number. This simple expression encapsulates the entire concept. Let's explore this further with examples.
Illustrative Examples: Bringing it to Life
Let's consider several examples to solidify our understanding:
-
Example 1: If the number is 15, then "a number decreased by 8" becomes 15 - 8 = 7.
-
Example 2: If the number is 22, the expression evaluates to 22 - 8 = 14.
-
Example 3: If the number is 5, then the result is 5 - 8 = -3. This example highlights the importance of understanding negative numbers in mathematics. Decreasing a small number by a larger number results in a negative outcome.
-
Example 4: If the number is 0, then the result is 0 - 8 = -8. This illustrates that even starting with zero, the operation still produces a result.
These examples demonstrate the straightforward application of the concept. However, the true power of understanding "a number decreased by 8" lies in its application within more complex mathematical scenarios.
Moving Beyond the Basics: Word Problems and Equations
The phrase "a number decreased by 8" frequently appears in word problems, requiring you to translate the verbal description into a mathematical equation. Let's consider a few scenarios:
- Word Problem 1: John had x apples. He gave away 8 apples. How many apples does John have left?
This translates directly into the equation: x - 8 = y, where y represents the number of apples John has left. To solve this, we need to know the initial number of apples (x).
- Word Problem 2: The temperature was x degrees Celsius. The temperature dropped by 8 degrees. What is the new temperature?
This again leads to the equation: x - 8 = z, where z represents the new temperature. Solving this requires knowing the initial temperature (x).
These examples highlight the importance of translating verbal descriptions into mathematical expressions. This skill is crucial for solving real-world problems that involve unknown quantities.
Solving Equations: Finding the Unknown
Often, word problems don't directly give you the value of the unknown number (x). Instead, they might provide the result of the operation ("a number decreased by 8 is 12," for example). This introduces the concept of solving equations.
Let's say we have the equation: x - 8 = 12. To solve for x, we need to isolate the variable. We can do this by adding 8 to both sides of the equation:
x - 8 + 8 = 12 + 8
This simplifies to:
x = 20
Therefore, the unknown number (x) is 20. This process of manipulating equations to isolate the variable is a fundamental skill in algebra.
Advanced Applications: Inequalities and Beyond
The concept extends beyond simple equations. It can be applied to inequalities as well. For example:
x - 8 > 5
This inequality reads as "a number decreased by 8 is greater than 5." To solve this, we add 8 to both sides:
x > 13
This means that x can be any number greater than 13. This demonstrates the application of the concept within the realm of inequalities. Furthermore, "a number decreased by 8" can also form part of more complex expressions and functions in higher-level mathematics.
The Significance of Negative Numbers
As seen in earlier examples, the result of "a number decreased by 8" can be a negative number. Understanding negative numbers is crucial for mastering this concept. Negative numbers represent values less than zero and play a vital role in various mathematical and real-world applications. They are essential for understanding concepts like debt, temperature below zero, and coordinates in a Cartesian plane.
Real-World Applications: Practical Examples
The concept of "a number decreased by 8" isn't confined to theoretical mathematical problems. It has numerous real-world applications:
-
Finance: Calculating remaining balance after a withdrawal of $8 from an account.
-
Temperature: Determining the temperature after an 8-degree drop.
-
Inventory: Calculating the remaining stock after selling 8 units.
-
Measurement: Finding the remaining length after cutting 8 centimeters from a piece of wood.
-
Game scores: Determining the score after losing 8 points.
These examples show that this seemingly simple mathematical concept has broad applicability in various aspects of our daily lives.
Frequently Asked Questions (FAQ)
-
Q: What if the number is negative?
A: The operation remains the same. For instance, if the number is -5, then "a number decreased by 8" becomes -5 - 8 = -13.
-
Q: Can I use different variables?
A: Absolutely! You can use any letter or symbol to represent the unknown number; x, y, n, or even a more descriptive variable like apples are all acceptable.
-
Q: How do I solve more complex equations involving "a number decreased by 8"?
A: Apply the principles of algebraic manipulation. Use inverse operations (addition to undo subtraction) to isolate the variable and solve for its value. Remember to perform the same operation on both sides of the equation to maintain balance.
-
Q: What are some common mistakes students make when working with this concept?
A: Common mistakes include incorrect subtraction (especially with negative numbers), misinterpreting word problems, and failing to isolate the variable correctly when solving equations.
-
Q: What are some resources to further improve my understanding?
A: Textbooks on pre-algebra and algebra, online educational videos, and practice exercises focusing on equation solving and word problems are valuable resources.
Conclusion: Mastering a Fundamental Concept
Understanding "a number decreased by 8" is more than just knowing how to perform a simple subtraction. It’s about grasping the fundamental principles of algebra, equation solving, and the application of these concepts to real-world scenarios. By mastering this seemingly simple concept, you build a solid foundation for more advanced mathematical studies and problem-solving skills. This understanding will serve as a stepping stone to tackling more complex mathematical problems and developing your analytical abilities. The ability to translate verbal descriptions into mathematical expressions and solve equations is invaluable, not only in mathematics but also in various fields that require problem-solving and analytical skills. Remember to practice regularly and seek help when needed – consistent effort is key to mastering this fundamental mathematical concept and building a solid foundation for your future mathematical endeavors.
Latest Posts
Latest Posts
-
What Is 3 Of 20
Sep 15, 2025
-
Examples Of Black Body Objects
Sep 15, 2025
-
Amino Acid With Hydroxyl Group
Sep 15, 2025
-
5x 2 3x 2 0
Sep 15, 2025
-
Glycogen Is An Example Of
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about A Number Decreased By 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.