What Is 3 Of 20
thesills
Sep 15, 2025 · 5 min read
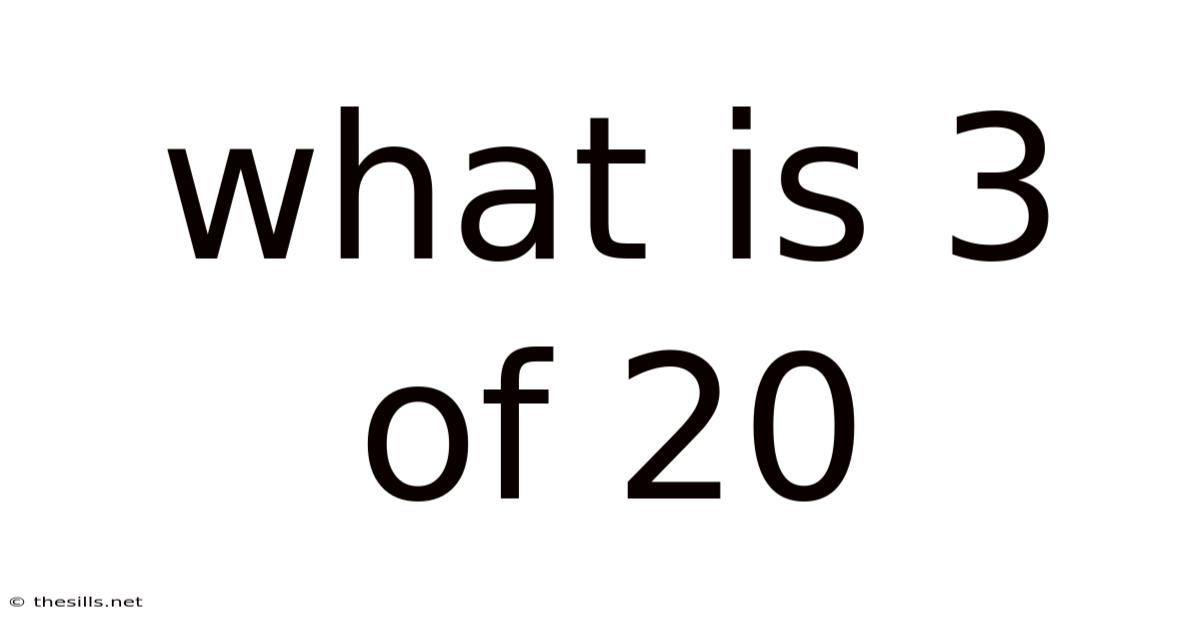
Table of Contents
What is 3 of 20? Understanding Fractions, Ratios, and Percentages
What is 3 of 20? This seemingly simple question opens the door to a deeper understanding of fundamental mathematical concepts like fractions, ratios, and percentages. While the immediate answer might seem obvious, exploring this question allows us to delve into the various ways we represent parts of a whole and their practical applications in everyday life. This article will explore this question thoroughly, providing clear explanations and examples to solidify your understanding.
Understanding the Basic Concepts
Before diving into the specifics of "3 of 20," let's establish a firm grasp of the core mathematical ideas involved.
-
Fractions: A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, ½ represents one out of two equal parts.
-
Ratios: A ratio compares two or more quantities. It shows the relative size of one quantity to another. Ratios can be expressed in different ways: using the colon symbol (e.g., 3:20), as a fraction (e.g., 3/20), or using the word "to" (e.g., 3 to 20).
-
Percentages: A percentage is a fraction or ratio expressed as a number out of 100. It represents a proportion of a whole and is denoted by the symbol "%". For instance, 50% means 50 out of 100, or ½.
Calculating 3 of 20: Different Perspectives
Now, let's tackle "3 of 20" using the concepts mentioned above:
1. As a Fraction:
"3 of 20" can be directly translated into a fraction: 3/20. This fraction represents three parts out of a total of twenty equal parts. This is the simplest and most direct representation of the problem.
2. As a Ratio:
The ratio of 3 to 20 is expressed as 3:20 or 3/20. This shows the relative proportion of 3 compared to 20. This is particularly useful when comparing different quantities or proportions.
3. As a Percentage:
To express "3 of 20" as a percentage, we need to convert the fraction 3/20 into a percentage. We do this by dividing the numerator by the denominator and then multiplying by 100:
(3 ÷ 20) x 100 = 15%
Therefore, 3 out of 20 is equivalent to 15%. This means that 3 represents 15% of the total quantity of 20.
4. Decimal Representation:
We can also represent 3/20 as a decimal. Dividing 3 by 20 gives us 0.15. This decimal representation is another way of expressing the proportion of 3 out of 20.
Real-World Applications
Understanding how to calculate "3 of 20" and similar proportions has numerous practical applications:
-
Shopping: Imagine a sale offering a 15% discount. If an item costs $20, the discount amount would be 15% of $20, which is $3 (as calculated above).
-
Surveys and Statistics: If a survey of 20 people reveals that 3 prefer a particular brand, this represents 15% preference for that brand.
-
Baking and Cooking: Recipe adjustments often involve scaling up or down. If a recipe calls for 20 units of an ingredient and you only want to use 3, you're using 15% of the original amount.
-
Finance: Calculating interest, returns on investments, or loan repayments often involves working with percentages and fractions. Understanding proportions is crucial for making informed financial decisions.
Further Exploration: Expanding the Concept
While the basic calculation of "3 of 20" is straightforward, we can expand our understanding by considering related concepts:
-
Finding the Whole: If we know that 3 represents 15% of a total quantity, we can work backward to find the whole. This involves using the concept of inverse proportions. If 15% is 3, then 1% would be 3/15 = 0.2, and 100% (the whole) would be 0.2 x 100 = 20. This confirms our original understanding that 3 is part of a whole of 20.
-
Comparing Proportions: We can compare different proportions to see which one is larger or smaller. For example, we could compare "3 of 20" with "5 of 25". Converting both into percentages (15% and 20%, respectively) reveals that "5 of 25" is a larger proportion than "3 of 20".
-
Complex Proportions: More complex problems may involve multiple proportions and require a step-by-step approach to solve. For instance, we might need to calculate a percentage of a percentage or combine different proportions to arrive at a final answer.
Frequently Asked Questions (FAQ)
Q: What if the numbers are not integers?
A: The same principles apply whether the numbers are integers or decimals. You can use the same methods (fractions, ratios, percentages) to determine the proportion. For instance, "1.5 of 10" can be expressed as the fraction 1.5/10, which simplifies to 3/20 (equivalent to 15%).
Q: Can this be applied to larger numbers?
A: Absolutely! The methods described above work equally well with larger numbers. The principle remains the same: express the part as a fraction, ratio, or percentage of the whole.
Q: What are the common mistakes when dealing with proportions?
A: Common mistakes include:
- Incorrectly identifying the numerator and denominator in a fraction.
- Miscalculating percentages.
- Not converting units consistently (e.g., mixing percentages with decimals).
- Failing to understand the context of the problem.
Q: How can I improve my understanding of proportions?
A: Practice is key! Solve various problems involving fractions, ratios, and percentages. Start with simple problems and gradually move towards more complex ones. Use visual aids like diagrams or charts to better understand the concepts.
Conclusion
Understanding "what is 3 of 20" extends far beyond a simple calculation. It's a gateway to understanding fractions, ratios, percentages, and their various applications in daily life. Mastering these fundamental mathematical concepts empowers you to solve problems, analyze data, and make informed decisions in a wide range of contexts. By applying the techniques described in this article and practicing regularly, you'll build a strong foundation in proportional reasoning, a critical skill for both academic success and real-world problem-solving. Remember to always approach problem-solving systematically, ensuring that you clearly understand the question and apply the appropriate mathematical tools. With consistent effort and practice, you'll become proficient in understanding and calculating proportions efficiently and accurately.
Latest Posts
Latest Posts
-
Why Is Nh3 A Base
Sep 15, 2025
-
Can Opportunity Cost Be Negative
Sep 15, 2025
-
Structure Of Ribose And Deoxyribose
Sep 15, 2025
-
Sodium Acetate With Hydrochloric Acid
Sep 15, 2025
-
Can All Living Things Breathe
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.