5x 2 3x 2 0
thesills
Sep 15, 2025 · 6 min read
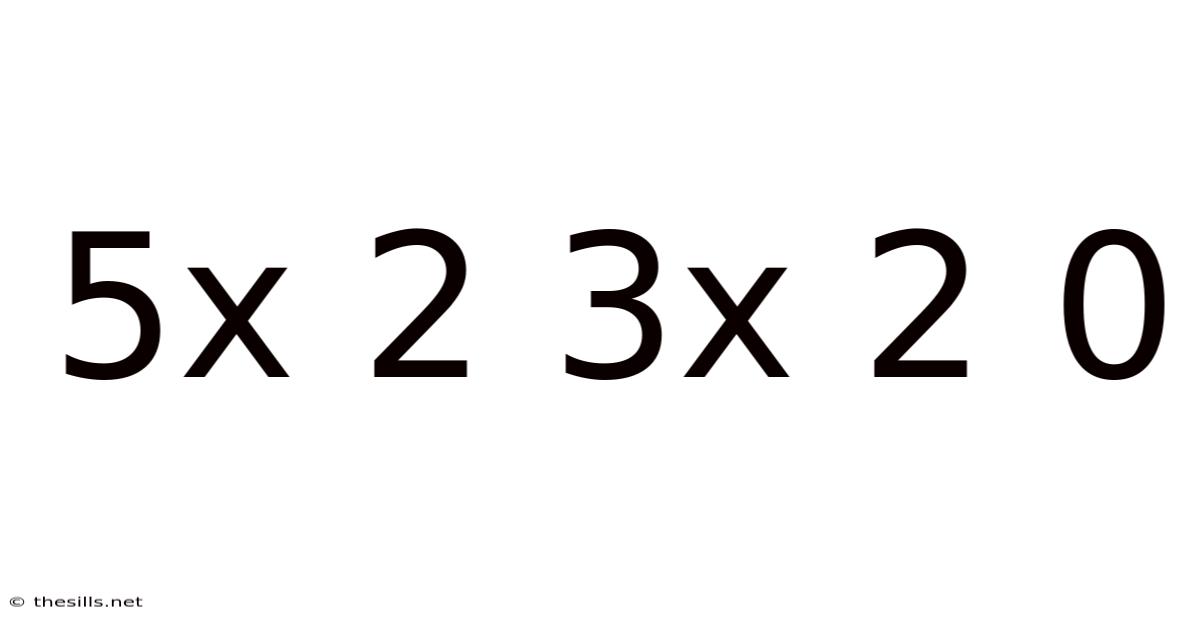
Table of Contents
Decoding the Mystery: 5x² + 3x² = 0 – A Deep Dive into Quadratic Equations
This article explores the seemingly simple equation 5x² + 3x² = 0, unraveling its mathematical implications and providing a comprehensive understanding of quadratic equations, their solutions, and their applications. We'll move beyond simply finding the answer to delve into the underlying concepts, offering a robust educational experience for students and anyone interested in strengthening their mathematical skills. This exploration will cover the fundamental principles, solution methods, and real-world applications of such equations.
Understanding the Fundamentals: What are Quadratic Equations?
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually x) is 2. The general form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a is not equal to zero (if a were zero, it would no longer be a quadratic equation). Our equation, 5x² + 3x² = 0, is a special case of a quadratic equation where b and c are both zero.
This seemingly simple equation presents a valuable opportunity to understand the core principles of solving quadratic equations. It allows us to focus on the manipulation of algebraic expressions and the significance of the solutions obtained.
Solving the Equation: Step-by-Step Process
Let's solve 5x² + 3x² = 0 step-by-step:
-
Combine like terms: The first step is to simplify the equation by combining the terms with x². Both 5x² and 3x² are like terms, meaning they have the same variable raised to the same power. Adding them together gives us:
8x² = 0
-
Isolate x²: To isolate x², we need to divide both sides of the equation by 8:
x² = 0
-
Solve for x: To find the value of x, we take the square root of both sides of the equation:
√x² = √0
x = 0
Therefore, the solution to the equation 5x² + 3x² = 0 is x = 0.
The Significance of the Solution and the Zero Product Property
The solution x = 0 might seem trivial at first glance. However, it's crucial to understand its significance in the context of quadratic equations and the zero product property. The zero product property states that if the product of two or more factors is zero, then at least one of the factors must be zero.
In our simplified equation, 8x² = 0, we can rewrite it as 8 * x * x = 0. According to the zero product property, this equation is only true if either 8 = 0 (which is false) or x = 0. This highlights the importance of the zero product property in solving quadratic equations – it allows us to break down complex equations into simpler factors and solve for the unknown variable.
Expanding Our Understanding: General Quadratic Equations and Solution Methods
While our initial equation was straightforward, let's expand our understanding by examining the general form of a quadratic equation: ax² + bx + c = 0. Several methods can be used to solve for x, including:
-
Factoring: If the quadratic expression can be factored easily, this is often the quickest method. Factoring involves rewriting the equation as a product of two linear expressions. For example, x² + 5x + 6 = 0 can be factored into (x + 2)(x + 3) = 0, leading to solutions x = -2 and x = -3.
-
The Quadratic Formula: The quadratic formula is a powerful tool that provides solutions for any quadratic equation, regardless of whether it can be factored easily. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
This formula provides two potential solutions, reflecting the possibility of a parabola (the graphical representation of a quadratic equation) intersecting the x-axis at two points, one point, or not at all (depending on the discriminant, b² - 4ac).
-
Completing the Square: Completing the square is a method used to manipulate the equation into a perfect square trinomial, making it easier to solve. This method is particularly useful when factoring isn't straightforward.
-
Graphical Methods: Quadratic equations can be solved graphically by plotting the corresponding parabola and identifying the x-intercepts (points where the parabola crosses the x-axis). These x-intercepts represent the solutions to the equation.
The Discriminant and the Nature of Roots
The discriminant (b² - 4ac) within the quadratic formula provides valuable information about the nature of the roots (solutions) of a quadratic equation:
-
b² - 4ac > 0: The equation has two distinct real roots. The parabola intersects the x-axis at two different points.
-
b² - 4ac = 0: The equation has one real root (a repeated root). The parabola touches the x-axis at only one point (its vertex).
-
b² - 4ac < 0: The equation has no real roots. The parabola does not intersect the x-axis. The roots are complex numbers involving the imaginary unit i (√-1).
Real-World Applications of Quadratic Equations
Quadratic equations are far from abstract mathematical concepts; they have numerous practical applications across various fields:
-
Physics: Calculating the trajectory of a projectile, determining the height of an object thrown upwards, and understanding the motion of objects under constant acceleration all involve quadratic equations.
-
Engineering: Designing bridges, parabolic antennas, and other structures often utilizes quadratic equations to model curves and optimize designs.
-
Business and Economics: Quadratic equations can model profit, revenue, and cost functions, helping businesses make informed decisions about pricing and production.
-
Computer Graphics: Creating curves and shapes in computer graphics often relies on quadratic equations and related mathematical concepts.
-
Data Analysis: Quadratic regression is used to model data that follows a parabolic trend.
Frequently Asked Questions (FAQs)
Q: What if the coefficient of x² is zero?
A: If the coefficient of x² (the a in ax² + bx + c = 0) is zero, the equation is no longer quadratic but becomes a linear equation. It can be solved using simpler algebraic techniques.
Q: Can a quadratic equation have more than two solutions?
A: No, a quadratic equation can have at most two solutions (roots). This is a fundamental property of quadratic functions.
Q: What if I get a negative number under the square root in the quadratic formula?
A: If you obtain a negative number under the square root in the quadratic formula, it means that the quadratic equation has no real solutions. The solutions are complex numbers, involving the imaginary unit i.
Q: Which method of solving quadratic equations is the best?
A: The best method depends on the specific equation. Factoring is easiest if the expression factors easily. The quadratic formula works for all quadratic equations but can be more time-consuming. Completing the square is useful when factoring is difficult.
Conclusion: Beyond the Surface
Our exploration of the equation 5x² + 3x² = 0 has taken us far beyond a simple algebraic calculation. We've delved into the core concepts of quadratic equations, their solution methods, the implications of the zero product property, and the rich tapestry of real-world applications. By understanding these concepts, we gain a stronger foundation in mathematics, preparing us to tackle more complex problems and appreciate the power and elegance of mathematical principles. This journey underscores the importance of not just finding the answer, but understanding the "why" behind the mathematics. The seemingly simple equation serves as a gateway to a deeper appreciation of quadratic equations and their significant role in various aspects of our world.
Latest Posts
Latest Posts
-
Why Is Nh3 A Base
Sep 15, 2025
-
Can Opportunity Cost Be Negative
Sep 15, 2025
-
Structure Of Ribose And Deoxyribose
Sep 15, 2025
-
Sodium Acetate With Hydrochloric Acid
Sep 15, 2025
-
Can All Living Things Breathe
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 5x 2 3x 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.