2x 3 3x 7 0
thesills
Sep 14, 2025 · 6 min read
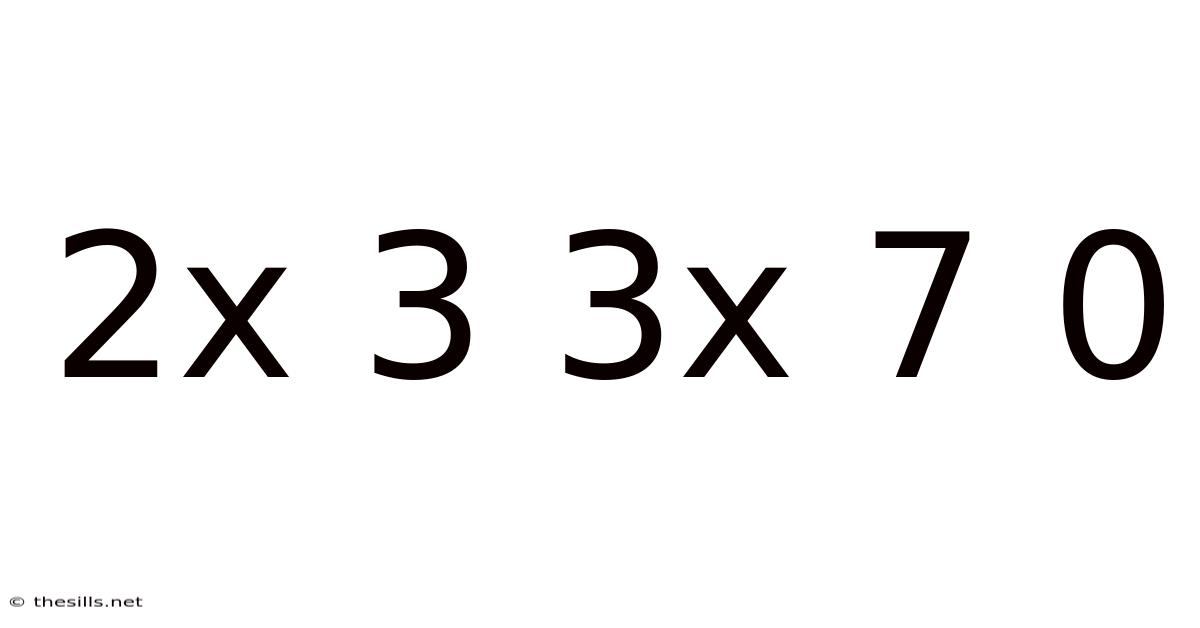
Table of Contents
Decoding the Mystery: 2x3, 3x7, 0 – A Deep Dive into Number Patterns, Mathematical Operations, and Problem-Solving Strategies
This article delves into the seemingly simple sequence "2x3, 3x7, 0," exploring its potential interpretations, underlying mathematical principles, and broader implications for problem-solving and critical thinking. We'll move beyond simple arithmetic to uncover the rich possibilities hidden within this enigmatic sequence and develop strategies for tackling similar number puzzles. Understanding this sequence unlocks a pathway to mastering more complex mathematical concepts and sharpening analytical skills.
Understanding the Basics: Multiplication and the Zero
Before embarking on an in-depth analysis, let's establish a firm grasp of the fundamentals. The sequence "2x3, 3x7, 0" involves basic multiplication. Multiplication, a fundamental arithmetic operation, represents repeated addition. For example, 2x3 means adding 2 three times (2+2+2 = 6), resulting in a product of 6. Similarly, 3x7 signifies adding 3 seven times (3+3+3+3+3+3+3 = 21). Zero, on the other hand, is a unique number representing the absence of quantity. It plays a crucial role in various mathematical concepts, including multiplication (where anything multiplied by zero equals zero) and addition (where adding zero does not change the value).
Potential Interpretations and Hidden Patterns:
The sequence’s simplicity is deceptive. There isn't one single definitive "answer" but several valid interpretations depending on the context and assumptions made. Let's explore some possibilities:
1. A Sequence of Multiplication Operations:
The most straightforward interpretation is that the sequence presents a series of distinct multiplication operations:
- 2 x 3 = 6
- 3 x 7 = 21
- 0 (This zero might represent a break in the pattern, an intentional inclusion, or a placeholder for an unknown value.)
This interpretation highlights the basic arithmetic involved but doesn't reveal any immediately obvious underlying pattern connecting the numbers.
2. A Pattern Based on the Products:
Let's focus on the results of the multiplication: 6 and 21. Is there a connection?
- We could examine the factors of each product. The factors of 6 are 1, 2, 3, and 6. The factors of 21 are 1, 3, 7, and 21. The only common factor is 3.
- We could also look at the differences: 21 - 6 = 15. This difference doesn't immediately suggest a clear pattern.
- We might consider the sums of the digits: 6 (6) and 21 (2+1=3). Again, no clear pattern emerges at first glance.
The presence of zero complicates the search for a discernible pattern among the products.
3. A Pattern Based on the Operands:
Instead of focusing on the products, let's analyze the operands (the numbers being multiplied): 2, 3, 3, 7.
- We could look for a relationship between consecutive numbers: 3-2 = 1, 7-3 = 4. This difference isn't consistent.
- Perhaps there's a pattern in the order of operations? The first operation uses smaller numbers (2 and 3), while the second uses larger numbers (3 and 7). The zero might signal a change in this pattern.
- We might even explore prime numbers. 3 and 7 are prime numbers, while 2 is the only even prime number. This might indicate a possible underlying pattern related to prime numbers, especially if we consider the zero as a termination point.
4. Considering Zero as a Placeholder or a Missing Number:
The presence of zero is intriguing. It could signify several things:
- A break in the pattern: The sequence might simply stop.
- A missing number: Perhaps there's a missing operation or a missing result in the sequence, which would necessitate solving for the unknown value.
- A mathematical operation: The zero could be the result of an operation not explicitly stated. For example, it might be derived by subtracting the first product from the second (21 - 6 = 15) or solving an equation involving the given values.
5. Contextual Considerations:
The interpretation might depend heavily on the context where this sequence is found. Is it part of a larger mathematical problem? Is it part of a coding sequence? Without additional information, multiple interpretations are possible.
Expanding the Possibilities: Introducing Algebraic Thinking
To further explore the possibilities, we can use algebraic reasoning. Let's assume a pattern exists and try to represent it using variables. Let's say the sequence follows the pattern:
- a x b = c
- d x e = f
- g
We know that a=2, b=3, c=6, d=3, e=7, f=21, and g=0. However, this doesn't help us uncover a consistent relationship between these variables. To find a pattern, we might need additional information or data points. Alternatively, we could hypothesize different mathematical relationships between these variables and attempt to verify them.
Developing Problem-Solving Strategies:
Tackling such number puzzles requires a systematic approach:
- Identify the givens: Clearly state the information provided (2x3, 3x7, 0).
- Look for patterns: Examine the relationships between the numbers – differences, sums, factors, prime numbers, etc.
- Formulate hypotheses: Develop possible interpretations based on your observations.
- Test your hypotheses: Check if your interpretations hold true for all the given numbers.
- Consider alternative approaches: If one approach fails, explore other mathematical concepts or problem-solving strategies (algebra, geometry, etc.)
- Seek additional information: If the puzzle lacks sufficient information, seek additional details or context.
Frequently Asked Questions (FAQ):
-
Q: Is there only one correct answer to this sequence?
- A: No, without additional context or information, there isn't a single definitive "answer." Multiple interpretations are plausible.
-
Q: What if the zero isn't significant?
- A: If we disregard the zero, we are left with two distinct multiplications with no immediately apparent connection.
-
Q: Could this sequence be part of a larger problem?
- A: Absolutely! This sequence could be a small piece of a more extensive mathematical problem requiring a deeper level of analysis and problem-solving techniques.
-
Q: How can I improve my skills in solving such number puzzles?
- A: Practice regularly, explore different mathematical concepts, and develop a systematic approach to problem-solving.
Conclusion:
The seemingly simple sequence "2x3, 3x7, 0" provides a rich platform for exploring mathematical thinking and problem-solving strategies. The ambiguity inherent in the sequence underscores the importance of critical thinking, creative interpretation, and the iterative process of formulating and testing hypotheses. While there isn't a singular solution, the journey of exploring its potential interpretations enhances one's mathematical understanding and sharpens problem-solving skills. The presence of zero adds an intriguing layer of complexity, prompting us to consider its potential meanings within the context of the sequence. This puzzle serves as a valuable reminder that in mathematics, as in life, there are often multiple perspectives and approaches to understanding any given situation. Continued exploration and a flexible approach to problem-solving are key to unlocking the hidden patterns and insights within this, and other, similar mathematical challenges. The quest for understanding transcends the simple act of calculating products; it's about nurturing analytical skills and developing a deeper appreciation for the power of mathematical thinking.
Latest Posts
Latest Posts
-
Integral Of Xsin 2x Dx
Sep 14, 2025
-
What Is Half In Decimals
Sep 14, 2025
-
3x 2 X 2 4
Sep 14, 2025
-
Reduction Of Ketone To Alcohol
Sep 14, 2025
-
15 Inches By 15 Inches
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2x 3 3x 7 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.