Integral Of Xsin 2x Dx
thesills
Sep 14, 2025 · 6 min read
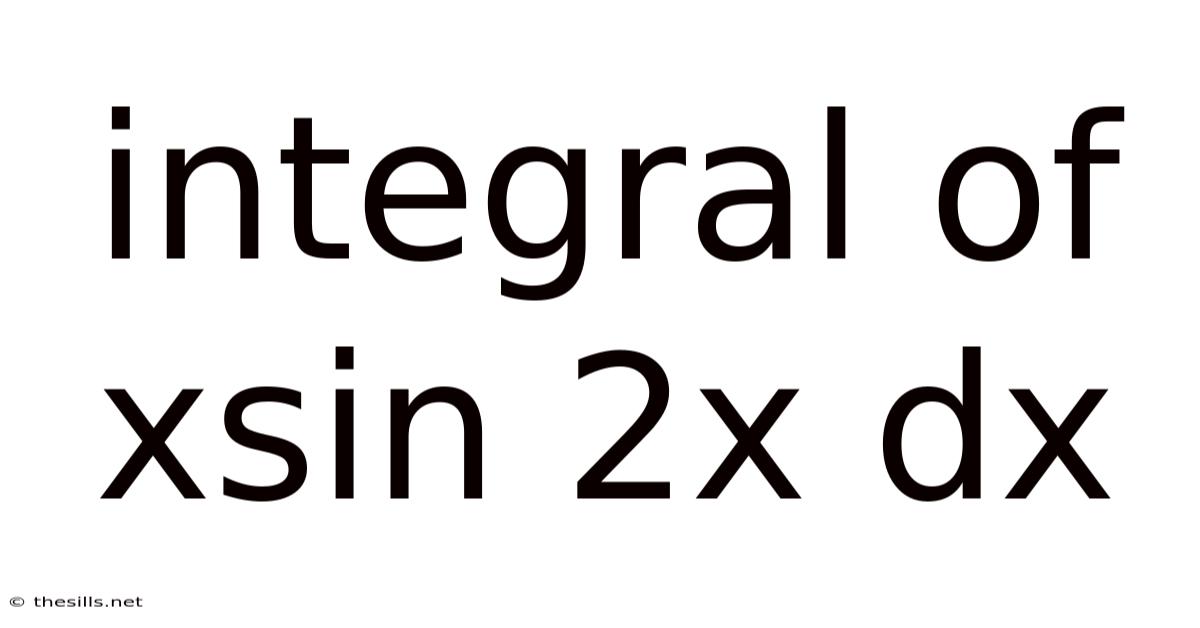
Table of Contents
Solving the Integral of x sin(2x) dx: A Comprehensive Guide
This article provides a comprehensive walkthrough of how to solve the integral ∫x sin(2x) dx. Understanding this integral is crucial for students of calculus and anyone working with trigonometric functions and integration techniques. We'll cover the necessary steps, explain the underlying principles, and explore common pitfalls to avoid. This detailed explanation will equip you with the skills to tackle similar integration problems.
Introduction: Understanding the Problem
The integral ∫x sin(2x) dx presents a challenge because it involves the product of a polynomial function (x) and a trigonometric function (sin(2x)). Direct integration isn't possible; we need a technique to simplify the expression before integrating. This is where integration by parts comes into play. We'll explore this method step-by-step, ensuring a clear understanding of each stage. This guide aims to be accessible to students with a foundational knowledge of calculus and trigonometry.
Integration by Parts: The Key Technique
Integration by parts is a powerful technique derived from the product rule of differentiation. It allows us to integrate products of functions by transforming the integral into a more manageable form. The formula for integration by parts is:
∫u dv = uv - ∫v du
Where 'u' and 'v' are functions of x. The key is to strategically choose 'u' and 'dv' to simplify the integral on the right-hand side.
Step-by-Step Solution: Applying Integration by Parts
Let's apply integration by parts to solve ∫x sin(2x) dx.
Step 1: Choosing u and dv
We need to choose 'u' and 'dv' carefully. A good rule of thumb is to choose 'u' as the function that simplifies when differentiated and 'dv' as the function that is easily integrated. In this case:
- u = x (because its derivative, du/dx = 1, is simpler)
- dv = sin(2x) dx (because its integral, v, is readily available)
Step 2: Finding du and v
Now, we find the derivative of 'u' and the integral of 'dv':
- du = dx (the derivative of x with respect to x)
- v = -1/2 cos(2x) (the integral of sin(2x) dx. Remember the chain rule for integration!)
Step 3: Applying the Integration by Parts Formula
Substituting our values into the integration by parts formula:
∫x sin(2x) dx = uv - ∫v du = x(-1/2 cos(2x)) - ∫(-1/2 cos(2x)) dx
Step 4: Simplifying and Integrating
Let's simplify and integrate the remaining integral:
∫x sin(2x) dx = -1/2 x cos(2x) + 1/2 ∫cos(2x) dx
The integral of cos(2x) is 1/2 sin(2x). Therefore:
∫x sin(2x) dx = -1/2 x cos(2x) + 1/2 (1/2 sin(2x)) + C
Step 5: Final Result
Simplifying the expression, we arrive at the final solution:
∫x sin(2x) dx = -1/2 x cos(2x) + 1/4 sin(2x) + C
where 'C' is the constant of integration. This constant represents the family of antiderivatives of x sin(2x).
Mathematical Explanation and Justification
The success of this method hinges on the careful selection of 'u' and 'dv'. The LIATE rule often helps in this process:
- Logarithmic functions
- Inverse trigonometric functions
- Algebraic functions (polynomials)
- Trigonometric functions
- Exponential functions
This order suggests prioritizing logarithmic functions for 'u', then inverse trigonometric, algebraic, and so on. In our case, the algebraic function (x) precedes the trigonometric function (sin(2x)), justifying our choice.
The integration by parts method essentially transforms a more complex integral into a simpler one that can be directly evaluated. The process leverages the relationship between differentiation and integration, ultimately leading to the solution. The constant of integration, 'C', is crucial because the derivative of a constant is zero. Therefore, any constant can be added to the antiderivative without changing its derivative.
Common Mistakes and How to Avoid Them
-
Incorrectly choosing u and dv: This is the most common mistake. Choosing the wrong functions can lead to a more complex integral, not a simpler one. Always consider the LIATE rule and choose 'u' to be a function that simplifies upon differentiation.
-
Errors in differentiation and integration: Double-check your derivative and integral calculations. Even a minor mistake can significantly impact the final result.
-
Forgetting the constant of integration (C): This is a crucial step, often overlooked. Remember that the indefinite integral represents a family of functions, all differing by a constant.
-
Sign errors: Be cautious with signs, particularly when integrating trigonometric functions or dealing with negative values. A misplaced negative sign can invalidate the entire solution.
Frequently Asked Questions (FAQ)
Q1: Can this integral be solved using other methods?
A1: While integration by parts is the most straightforward approach for this specific integral, other methods might be possible but would likely be more convoluted. There is no simpler or more efficient method for this particular problem.
Q2: What if the argument of the sine function was different (e.g., sin(3x) or sin(x))?
A2: The procedure remains largely the same. The only difference would lie in the integral of 'dv' (the integral of the trigonometric function). For example, if it was sin(3x), the integral would be -1/3cos(3x).
Q3: Why is the constant of integration important?
A3: The constant of integration represents the family of antiderivatives. Without it, the solution represents only one specific antiderivative, neglecting the infinite number of others that differ only by a constant.
Q4: Can this method be applied to other integrals involving products of functions?
A4: Yes, absolutely. Integration by parts is a widely applicable technique used to solve integrals involving products of various functions, including exponential and logarithmic functions.
Q5: What if I get stuck during the process?
A5: Don't panic! Carefully review each step. Ensure you correctly chose 'u' and 'dv', and meticulously check your calculations for differentiation and integration. If you're still struggling, try working through the problem with a different approach, or consult relevant learning materials.
Conclusion: Mastering Integration Techniques
Solving the integral ∫x sin(2x) dx requires a clear understanding of integration by parts. This comprehensive guide not only provides a step-by-step solution but also delves into the underlying mathematical principles and emphasizes common pitfalls to avoid. By mastering this technique, you'll be well-equipped to tackle a wide range of similar integration problems, solidifying your understanding of calculus and integral calculus. Remember to practice regularly, and don't hesitate to consult additional resources or seek assistance when needed. The more you practice, the more intuitive and effortless integration by parts will become. Continuous practice is key to mastery in calculus.
Latest Posts
Latest Posts
-
1 15th Of A Second
Sep 14, 2025
-
Which Phase Changes Are Endothermic
Sep 14, 2025
-
Four More Than A Number
Sep 14, 2025
-
Derivative Of Sin X 1
Sep 14, 2025
-
Is No2 Ewg Or Edg
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Integral Of Xsin 2x Dx . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.