Four More Than A Number
thesills
Sep 14, 2025 · 6 min read
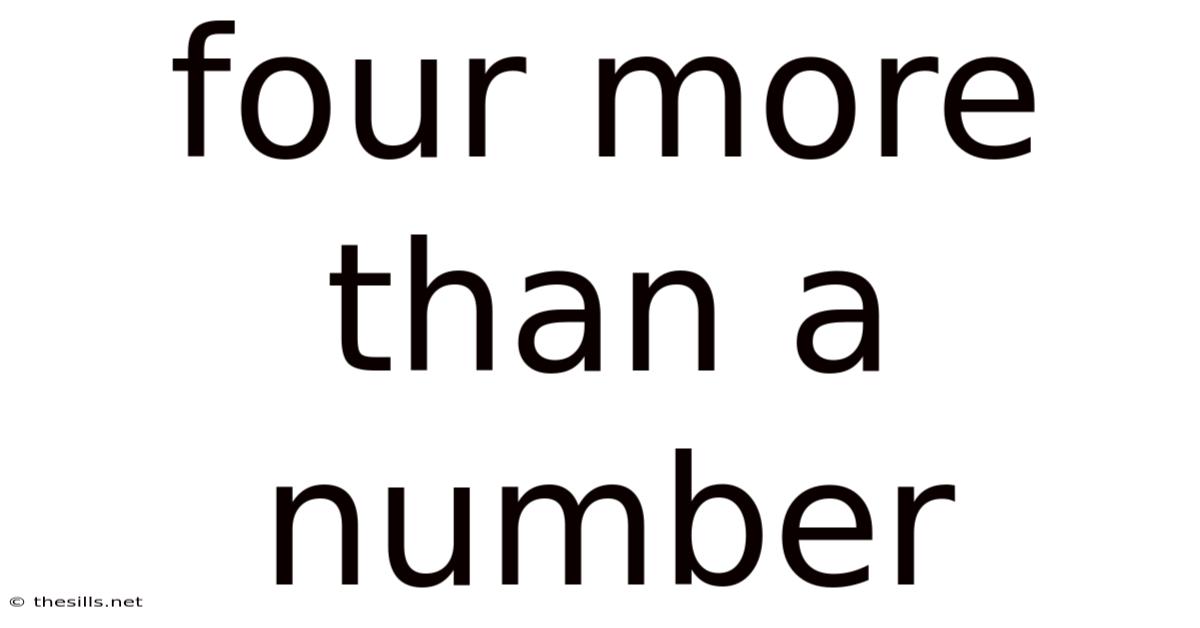
Table of Contents
Four More Than a Number: Exploring the Concept in Math and Beyond
Understanding the simple phrase "four more than a number" might seem trivial at first glance. However, this seemingly basic concept forms the foundation for a wide range of mathematical operations, problem-solving strategies, and even abstract thinking. This article will delve deep into this concept, exploring its mathematical representation, its applications in various problem scenarios, and its importance in developing a strong mathematical foundation. We'll uncover the nuances of translating words into algebraic expressions, solving equations involving this concept, and even touch upon its conceptual significance in higher-level mathematics.
Understanding the Core Concept: "Four More Than a Number"
At its heart, "four more than a number" signifies the addition of four to an unknown quantity. This unknown quantity is typically represented by a variable, most commonly x. Therefore, the phrase translates directly into the algebraic expression: x + 4. This seemingly simple expression is the cornerstone for understanding how we represent verbal descriptions mathematically. It lays the groundwork for more complex equations and problem-solving strategies.
Representing "Four More Than a Number" Algebraically
The beauty of algebra lies in its ability to transform ambiguous word problems into precise mathematical statements. The phrase "four more than a number" is a perfect illustration of this. Let's break down the process:
- Identify the unknown: The phrase highlights an "unknown number," which we represent algebraically as x.
- Interpret the operation: "More than" indicates addition.
- Combine the elements: This gives us the algebraic expression: x + 4.
This simple expression can now be manipulated and used within larger equations to solve a variety of problems.
Solving Equations Involving "Four More Than a Number"
The expression x + 4 becomes part of a larger equation when we introduce a relationship to the unknown quantity. Let's explore a few examples:
Example 1: Simple Equation
"Four more than a number is equal to 9." This translates into the equation: x + 4 = 9. To solve for x, we subtract 4 from both sides of the equation:
x + 4 - 4 = 9 - 4
x = 5
Therefore, the number is 5.
Example 2: Equation with Multiple Steps
"Three times four more than a number is 21." This translates into: 3(x + 4) = 21. This requires multiple steps to solve:
- Distribute the 3: 3x + 12 = 21
- Subtract 12 from both sides: 3x = 9
- Divide both sides by 3: x = 3
Thus, the number is 3.
Example 3: Equation with a Negative Result
"Four more than a number is -2." This translates to: x + 4 = -2. Solving for x:
x + 4 - 4 = -2 - 4
x = -6
This demonstrates that the unknown number can also be negative.
Word Problems Involving "Four More Than a Number"
The true power of understanding "four more than a number" lies in its application to real-world scenarios. Let’s consider some examples:
Example 1: Age Problem
"John is four years older than Mary. If Mary is 12 years old, how old is John?"
Here, Mary's age (x) is the unknown, and John's age is represented by x + 4. Since Mary is 12, we have:
12 + 4 = 16
John is 16 years old.
Example 2: Geometry Problem
"The length of a rectangle is four centimeters more than its width. If the width is 7 centimeters, what is the length?"
Similar to the previous example, the width (x) is the unknown, and the length is x + 4. With a width of 7 cm, the length is:
7 + 4 = 11
The length of the rectangle is 11 centimeters.
Example 3: Financial Problem
"Sarah has four dollars more than David. If Sarah has 15 dollars, how much money does David have?"
Here, David's money (x) is the unknown, and Sarah's money is x + 4. Therefore:
x + 4 = 15
x = 11
David has 11 dollars.
Expanding the Concept: Variations and Extensions
The core concept of "four more than a number" can be extended in various ways:
- Different constants: Instead of four, we can use any other number. For example, "seven more than a number" becomes x + 7.
- Subtraction: The opposite of "more than" is "less than." "Four less than a number" translates to x - 4.
- Combined operations: More complex word problems involve a combination of addition, subtraction, multiplication, and division, all based on variations of this core concept. For example, "Twice the number that is four more than x" would be 2(x+4).
- Inequalities: The concept can also be applied to inequalities. "Four more than a number is greater than 10" would be expressed as x + 4 > 10.
The Importance of Conceptual Understanding
While mastering the mechanics of solving equations is essential, a deep conceptual understanding is even more crucial. Understanding the translation from words to algebraic expressions allows students to approach more complex problems with confidence. This ability is fundamental to success in higher-level mathematics and problem-solving in various fields.
Frequently Asked Questions (FAQ)
Q1: What if the number is negative?
A1: The concept applies equally to negative numbers. For instance, "four more than -3" is -3 + 4 = 1.
Q2: Can "four more than a number" be represented in other ways?
A2: While x + 4 is the most common representation, you could also write it as 4 + x due to the commutative property of addition.
Q3: How does this concept relate to other mathematical concepts?
A3: It's foundational to linear equations, functions, and even calculus. Understanding this basic concept is crucial for building a strong mathematical foundation.
Q4: What are some common mistakes students make?
A4: Common errors include misinterpreting "more than" as subtraction, incorrectly applying the order of operations (PEMDAS/BODMAS), and struggling with translating word problems into algebraic expressions.
Conclusion: A Foundation for Mathematical Success
The seemingly simple phrase "four more than a number" offers a powerful introduction to the world of algebra and problem-solving. By mastering the translation from words to algebraic expressions and practicing solving equations, students build a strong foundation for tackling more complex mathematical concepts. This understanding isn't just about solving equations; it’s about developing critical thinking skills, logical reasoning, and a deeper appreciation for the power of mathematics to model and solve real-world problems. The ability to translate words into mathematical symbols is a cornerstone of mathematical literacy and a crucial skill for success in various academic and professional pursuits. The seemingly simple concept of "four more than a number" is, in reality, a stepping stone to a much broader understanding of mathematics and its applications.
Latest Posts
Latest Posts
-
Decomposers Role In An Ecosystem
Sep 14, 2025
-
Animals Are Better Than Humans
Sep 14, 2025
-
Is Ch3 A Strong Base
Sep 14, 2025
-
What Is 5 Of 225
Sep 14, 2025
-
X 4 3x 2 2
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Four More Than A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.