X 4 3x 2 2
thesills
Sep 14, 2025 · 6 min read
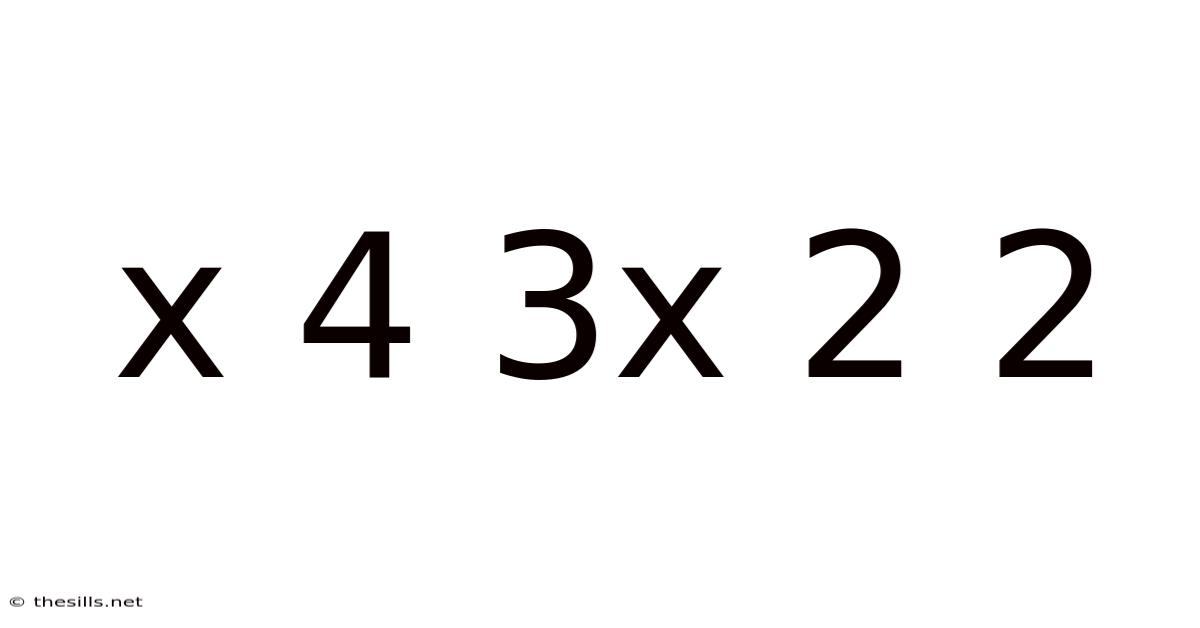
Table of Contents
Decoding the Mathematical Expression: x⁴ + 3x² + 2
This article delves into the fascinating world of polynomial expressions, specifically focusing on the seemingly simple yet richly nuanced equation: x⁴ + 3x² + 2. We will explore its various aspects, from basic factorization to advanced applications, providing a comprehensive understanding accessible to a wide range of readers. This exploration will include techniques for solving, analyzing its graphical representation, and discussing its relevance in various mathematical contexts.
I. Introduction: Understanding Polynomial Expressions
Before diving into the specifics of x⁴ + 3x² + 2, let's establish a foundational understanding of polynomial expressions. A polynomial is an algebraic expression consisting of variables (like 'x') and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents. Our expression, x⁴ + 3x² + 2, is a polynomial of degree 4, meaning the highest power of the variable 'x' is 4. This type of polynomial is also known as a quartic polynomial. Understanding polynomials is crucial in various fields, including calculus, physics, engineering, and computer science.
II. Factoring the Polynomial: A Step-by-Step Approach
Factoring a polynomial involves expressing it as a product of simpler polynomials. This process is essential for solving equations, simplifying expressions, and gaining deeper insights into the polynomial's behavior. Let's factor x⁴ + 3x² + 2. Notice that this polynomial is actually a quadratic in disguise. If we let u = x², then the expression becomes u² + 3u + 2. This is a much simpler quadratic expression that we can easily factor.
- Step 1: Identify the Quadratic Structure: Recognize that the expression can be treated as a quadratic in terms of x².
- Step 2: Factor the Quadratic: We look for two numbers that add up to 3 (the coefficient of u) and multiply to 2 (the constant term). These numbers are 1 and 2. Therefore, u² + 3u + 2 factors as (u + 1)(u + 2).
- Step 3: Substitute Back: Remember that u = x². Substituting this back into the factored form gives us (x² + 1)(x² + 2).
Therefore, the complete factorization of x⁴ + 3x² + 2 is (x² + 1)(x² + 2). This factorization reveals important information about the polynomial's roots (or zeros), as we'll see later.
III. Finding the Roots (Zeros) of the Polynomial
The roots or zeros of a polynomial are the values of 'x' that make the polynomial equal to zero. Finding the roots is a critical step in understanding the behavior of the polynomial. To find the roots of x⁴ + 3x² + 2, we set the factored form equal to zero:
(x² + 1)(x² + 2) = 0
This equation is satisfied if either (x² + 1) = 0 or (x² + 2) = 0.
- Solving x² + 1 = 0: This gives x² = -1. The solutions are x = i and x = -i, where 'i' is the imaginary unit (√-1).
- Solving x² + 2 = 0: This gives x² = -2. The solutions are x = √2i and x = -√2i.
Therefore, the roots of the polynomial x⁴ + 3x² + 2 are i, -i, √2i, and -√2i. These are all complex roots, meaning they involve the imaginary unit 'i'. This indicates that the graph of the polynomial will not intersect the x-axis (the real number line).
IV. Graphical Representation and Analysis
The graph of x⁴ + 3x² + 2 provides a visual representation of the polynomial's behavior. Since all roots are complex, the graph will never cross the x-axis. It will be a curve entirely above the x-axis, exhibiting a characteristic "U" shape that's typical of even-degree polynomials with positive leading coefficients. The curve will have a minimum point, representing the lowest value the function takes on. Finding the exact coordinates of this minimum point requires calculus (finding the derivative and setting it to zero).
The graph illustrates the polynomial's positivity for all real values of x, a consequence of its factorization and the nature of its roots. This visual representation helps in understanding the polynomial's behavior across its domain.
V. Applications in Various Fields
Polynomials, including quartic polynomials like x⁴ + 3x² + 2, have numerous applications across diverse fields:
- Engineering: Polynomial equations are used to model various physical phenomena, including the displacement of a vibrating object, the trajectory of a projectile, and the stress distribution in a structure.
- Computer Science: Polynomials are fundamental in computer graphics, numerical analysis, and algorithm design. They are used in interpolation, approximation, and solving complex equations.
- Physics: Polynomial equations appear in classical mechanics, electromagnetism, and quantum mechanics, often used to approximate solutions to more complex problems.
- Economics: Polynomial functions can model economic growth, cost functions, and other economic relationships.
- Statistics: Polynomials are used in regression analysis, fitting curves to data sets, and constructing statistical models.
VI. Expanding the Understanding: Related Concepts
Understanding x⁴ + 3x² + 2 involves exploring several interconnected mathematical concepts:
- Complex Numbers: The presence of imaginary roots highlights the importance of complex numbers in algebra and their relevance in solving polynomial equations.
- Quadratic Formula: Although not directly used in this specific case, understanding the quadratic formula (used for solving second-degree polynomials) provides a foundation for tackling more complex polynomial equations.
- Fundamental Theorem of Algebra: This theorem states that a polynomial of degree 'n' has exactly 'n' roots (counting multiplicity), which is evident in our analysis of x⁴ + 3x² + 2 having four roots.
- Partial Fraction Decomposition: While not directly applicable here (since we have already factored the polynomial), this technique is crucial for working with rational functions which involves polynomials in the numerator and denominator.
VII. Frequently Asked Questions (FAQ)
Q1: Can this polynomial be factored in any other way?
A1: The factorization (x² + 1)(x² + 2) is the most straightforward and complete factorization using real coefficients. Further factorization would involve complex numbers.
Q2: What is the significance of the complex roots?
A2: The complex roots indicate that the graph of the polynomial doesn't intersect the x-axis. They are still important solutions to the equation x⁴ + 3x² + 2 = 0, playing a role in complete mathematical solutions and certain applications in advanced areas of mathematics and physics.
Q3: How can I find the minimum value of the function?
A3: Finding the minimum value requires using calculus. You'd need to find the first derivative, set it equal to zero, and solve for x. Then, substitute this x value back into the original polynomial to find the corresponding minimum y-value.
Q4: Are there any real-world applications directly related to this specific polynomial?
A4: While this specific polynomial might not have a direct, readily identifiable real-world application, it serves as a strong illustrative example for understanding the broader concepts related to polynomial functions, which are widely applied in various fields as explained earlier.
VIII. Conclusion: A Deeper Dive into Polynomial Analysis
This detailed analysis of the polynomial expression x⁴ + 3x² + 2 has provided a journey through factorization, root finding, graphical interpretation, and relevant applications. The seemingly simple equation unfolds to reveal deeper mathematical connections and demonstrates the power of polynomial analysis in various contexts. By understanding this example, readers can build a solid foundation for tackling more complex polynomial expressions and their significance in mathematics and its applications. The exploration of complex numbers and their role in the complete solution underscores the richness and depth of even seemingly simple mathematical expressions. This journey into the world of polynomials highlights the elegance and practicality of algebraic techniques, showcasing their power to unlock insights into a range of problems across multiple disciplines.
Latest Posts
Latest Posts
-
When Kcl Dissolves In Water
Sep 14, 2025
-
What Are The Accessory Organs
Sep 14, 2025
-
Bacterial Flagella Vs Eukaryotic Flagella
Sep 14, 2025
-
Why Enzymes Are Called Biocatalyst
Sep 14, 2025
-
Dorsal Blood Vessel Earthworm Function
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X 4 3x 2 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.