3x 2 X 2 4
thesills
Sep 14, 2025 · 6 min read
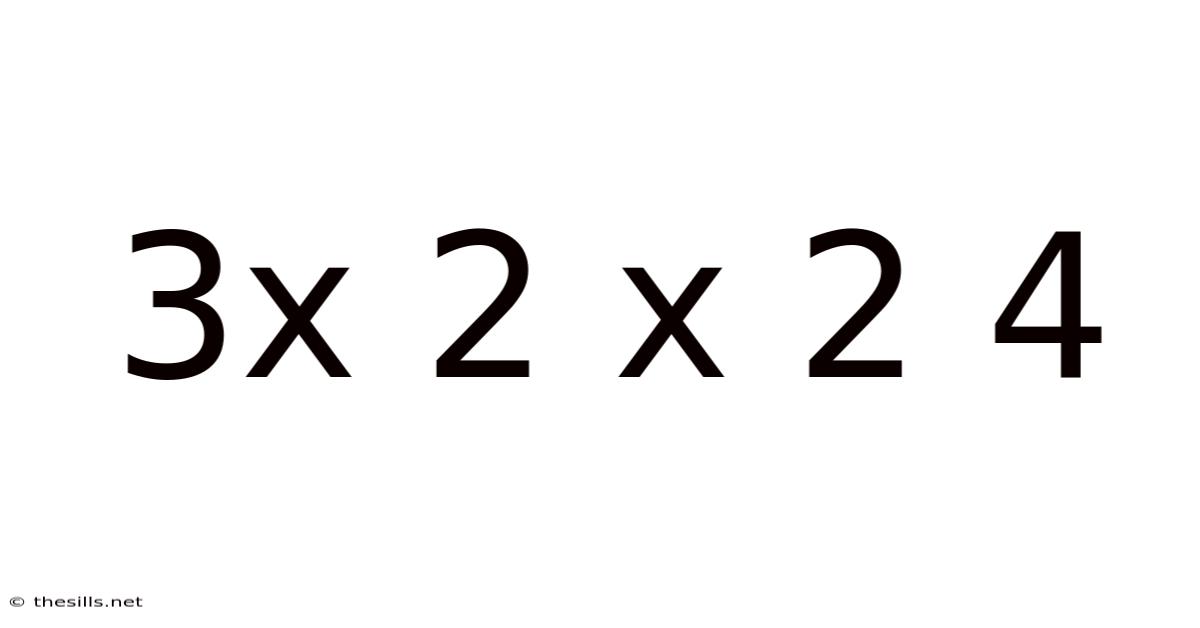
Table of Contents
Decoding the Seemingly Simple: Exploring the Mathematical Puzzle of "3 x 2 x 2 = 4"
This article delves into the intriguing mathematical statement "3 x 2 x 2 = 4," which at first glance appears incorrect. We will explore why this equation is initially perplexing, dissect the potential interpretations and underlying mathematical concepts, and examine various scenarios where such a statement might hold a degree of validity within specific contexts. Understanding this seemingly simple equation will require us to explore different mathematical perspectives and appreciate the importance of context in mathematical reasoning.
The Apparent Contradiction: Why 3 x 2 x 2 ≠ 12
Standard arithmetic dictates that 3 multiplied by 2, multiplied by 2, equals 12. This is a fundamental principle taught in elementary mathematics. Therefore, the statement "3 x 2 x 2 = 4" directly contradicts this basic arithmetic rule. This immediate contradiction is precisely what makes this puzzle so fascinating and prompts us to look beyond the obvious.
Potential Interpretations and Contextual Analysis
The key to unlocking this puzzle lies in exploring potential contexts where the equation might hold true, even if it contradicts standard arithmetic. Let's examine several possibilities:
1. Modular Arithmetic: A World Beyond Remainders
Modular arithmetic, often referred to as clock arithmetic, operates within a defined modulus. This means calculations are performed, and the results are reduced to the remainder after division by the modulus. For instance, in modulo 4 arithmetic (mod 4), any number is equivalent to its remainder when divided by 4.
Let's consider the equation within the context of mod 4:
- 3 x 2 x 2 = 12
When 12 is divided by 4, the remainder is 0. However, in mod 4, 0 is equivalent to 4. Therefore, within the framework of modulo 4 arithmetic, 3 x 2 x 2 ≡ 4 (mod 4). This equivalence holds true within this specific mathematical system. This highlights the importance of specifying the mathematical system when dealing with mathematical expressions.
2. Symbolic Representation and Hidden Operations
The equation could represent a more complex symbolic system. The numbers and symbols might represent elements in an abstract algebraic structure. In this case, the "x" symbol might not represent standard multiplication but a different operation entirely. For example:
- Let's define a new operation, '⊗', such that a ⊗ b = (a + b) mod 4.
Applying this new operation to our equation:
- 3 ⊗ 2 ⊗ 2 = (3 + 2) mod 4 ⊗ 2 = 1 ⊗ 2 = (1 + 2) mod 4 = 3
This still doesn't yield 4. However, this demonstrates how a different operational definition can completely change the outcome. The equation "3 x 2 x 2 = 4" could be a shorthand representation of a more intricate mathematical operation or system not immediately apparent from its simplistic form.
3. Error in Transcription or Presentation
The simplest and most likely explanation is an error. The equation could be a typographical error, a miscommunication, or a deliberate puzzle designed to highlight the importance of verifying mathematical statements. In this case, the equation is simply incorrect based on the standard rules of arithmetic.
4. Encoding and Cryptography
While less likely, the equation could be part of a simple code or cipher. The numbers could represent letters or symbols according to a substitution key. The equation itself is then part of a message requiring decoding. This interpretation suggests looking beyond the inherent mathematical properties and considering a completely different communicative context.
Exploring Related Mathematical Concepts
Understanding this puzzle necessitates exploring related mathematical concepts, further broadening our understanding of numbers and operations:
-
Order of Operations (PEMDAS/BODMAS): This rule governs the sequence of calculations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction). In our example, the order of operations does not affect the outcome since only multiplication is involved.
-
Associative and Commutative Properties: The associative property states that the grouping of numbers in multiplication does not affect the result (a x (b x c) = (a x b) x c). The commutative property states that the order of numbers in multiplication does not affect the result (a x b = b x a). Both properties are valid in standard arithmetic, but their application doesn't resolve the discrepancy between 12 and 4.
-
Distributive Property: This property states that a(b + c) = ab + ac. It is not directly applicable in solving this specific puzzle, but it's a crucial property in algebraic manipulation.
-
Boolean Algebra: This branch of algebra deals with binary values (true/false, 1/0). It’s possible that, within a Boolean system with redefined operators, the equation could have a valid interpretation.
Frequently Asked Questions (FAQ)
Q: Is it possible for 3 x 2 x 2 to ever equal 4?
A: Within the context of standard arithmetic, no. However, as demonstrated above, it can hold true within specific mathematical systems such as modular arithmetic, given a specific modulus.
Q: What are the practical applications of modular arithmetic?
A: Modular arithmetic finds significant applications in cryptography, computer science (particularly in hash functions and checksums), and number theory. It's fundamental to many aspects of modern technology and mathematics.
Q: Why is understanding the limitations of mathematical systems important?
A: Recognizing the limitations of a specific mathematical system is crucial for avoiding errors and ensuring accurate results. Different mathematical systems operate under different rules and assumptions. Applying the rules of one system to another can lead to incorrect conclusions.
Q: Can this puzzle be solved without altering the basic rules of arithmetic?
A: No. Without modifying the definition of the multiplication operation or introducing a different mathematical system, 3 x 2 x 2 will always equal 12 in standard arithmetic.
Conclusion: Embracing Mathematical Ambiguity
The seemingly simple equation "3 x 2 x 2 = 4" serves as a powerful illustration of the importance of context and the limitations of applying rules from one mathematical system to another. While it initially appears incorrect in standard arithmetic, we've explored various interpretations and mathematical systems where it might hold a degree of validity. This puzzle highlights the richness and complexity of mathematics, encouraging us to think critically, question assumptions, and appreciate the beauty of exploring diverse mathematical frameworks. The initial apparent contradiction ultimately leads us to a deeper appreciation of the nuanced nature of mathematical truth. It isn't always absolute and straightforward; often, it's highly dependent on the chosen system and the context within which we operate. This exploration underscores the significance of clear communication and precise definition in mathematics, preventing ambiguity and fostering deeper mathematical understanding. It's not about finding a single "correct" answer but appreciating the multiple perspectives and interpretations that can be uncovered by thoughtfully analyzing even a seemingly simple equation.
Latest Posts
Latest Posts
-
1 15th Of A Second
Sep 14, 2025
-
Which Phase Changes Are Endothermic
Sep 14, 2025
-
Four More Than A Number
Sep 14, 2025
-
Derivative Of Sin X 1
Sep 14, 2025
-
Is No2 Ewg Or Edg
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 3x 2 X 2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.