1 024 Divided By 32
thesills
Sep 18, 2025 · 6 min read
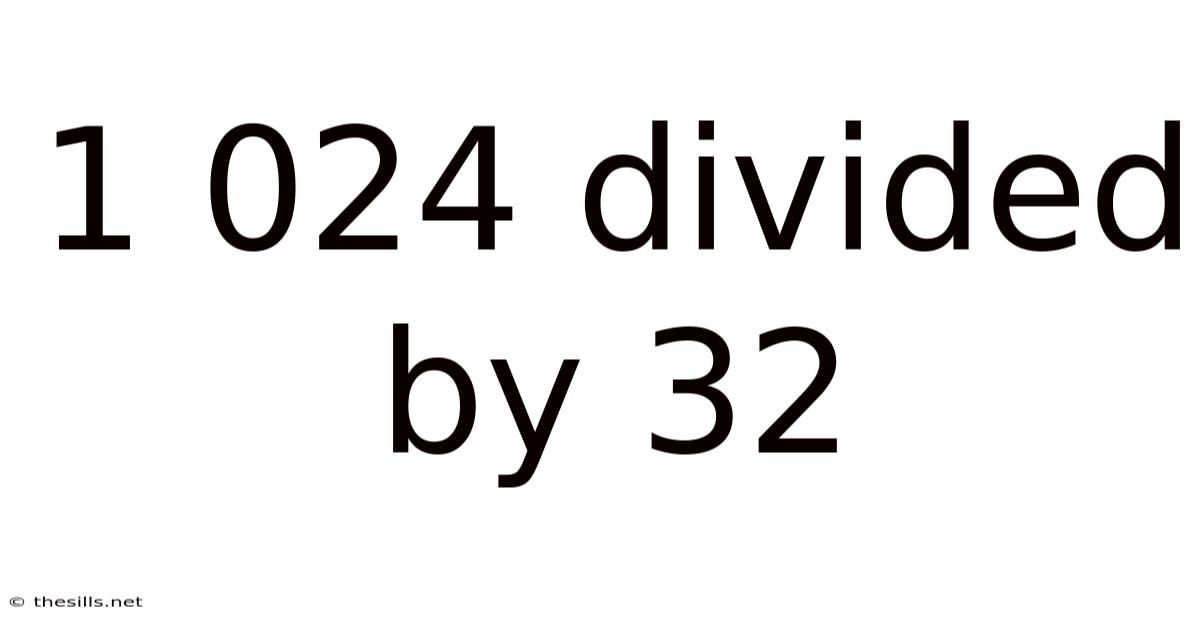
Table of Contents
Unveiling the Mystery: 1024 Divided by 32
This seemingly simple division problem, 1024 divided by 32, holds more significance than initially meets the eye. It's a fundamental calculation frequently encountered in computer science, mathematics, and even everyday problem-solving. This comprehensive guide will not only provide the answer but also delve into the underlying principles, explore different methods of solving it, and discuss its real-world applications. Understanding this seemingly basic calculation unlocks a deeper understanding of binary systems, data management, and numerical reasoning.
Introduction: Why is 1024/32 Important?
The numbers 1024 and 32 are pivotal in the digital world. 1024 (or 2<sup>10</sup>) is a power of two, representing a kilobyte in computer memory. 32 is also a power of two (2<sup>5</sup>), often used in various computing contexts such as bit representation and memory addressing. Understanding their relationship is crucial for grasping concepts like data storage, memory allocation, and efficient programming. This division problem is, therefore, a gateway to understanding fundamental computational principles.
Method 1: Long Division
The most straightforward approach is long division. While seemingly tedious for larger numbers, it reinforces fundamental arithmetic principles.
32
32 | 1024
-96
---
64
-64
---
0
This shows that 1024 divided by 32 equals 32.
Method 2: Simplifying with Powers of Two
Recognizing that both 1024 and 32 are powers of two significantly streamlines the calculation. We can rewrite the problem as:
(2<sup>10</sup>) / (2<sup>5</sup>)
Using the rule of exponents (a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>), we get:
2<sup>10-5</sup> = 2<sup>5</sup> = 32
This method demonstrates a more elegant and efficient approach, highlighting the power of understanding exponential notation.
Method 3: Using a Calculator
For quick solutions, a calculator provides the most immediate answer. Simply input "1024 / 32" and the calculator will instantly return 32. This method, while efficient, lacks the educational value of the previous methods, which illuminate the underlying mathematical principles.
The Significance of Powers of Two in Computing
The prevalence of powers of two in computing stems from the binary number system, which uses only two digits (0 and 1) to represent all data. Computers operate using transistors, which are essentially on/off switches. These on/off states are perfectly represented by binary digits (bits). Therefore, data storage and processing are organized in powers of two:
- Bit: The smallest unit of data, representing 0 or 1.
- Byte: 8 bits (2<sup>3</sup>).
- Kilobyte (KB): 1024 bytes (2<sup>10</sup>).
- Megabyte (MB): 1024 kilobytes (2<sup>20</sup>).
- Gigabyte (GB): 1024 megabytes (2<sup>30</sup>).
- Terabyte (TB): 1024 gigabytes (2<sup>40</sup>).
And so on. This system provides a highly efficient and logical structure for data management within computers. The division of 1024 by 32, therefore, could represent the conversion of a larger data unit into a smaller one, such as converting kilobytes to a smaller unit depending on the context (e.g., converting kilobytes into 32-byte blocks).
Real-World Applications: Beyond the Classroom
Understanding this calculation transcends simple arithmetic. Here are some real-world applications:
- Memory Allocation: In programming, memory is often allocated in blocks of sizes that are powers of two. Dividing a larger memory block (e.g., 1024 bytes) into smaller, equally sized blocks (e.g., 32 bytes each) is a common task in memory management. This division helps in efficiently distributing memory resources to different processes or data structures.
- Data Transfer Rates: Network speeds and data transfer rates are frequently expressed in multiples of powers of two (kilobits per second, megabits per second, etc.). Understanding these units requires familiarity with these fundamental calculations.
- Image Resolution: Image resolutions are often expressed in terms of pixels, which are organized in a grid structure. Calculations involving powers of two are common when dealing with image resizing, compression, and manipulation.
- Game Development: In game development, game engines often use power-of-two textures and other assets for optimal performance. Calculations involving powers of two are crucial for efficient resource management.
- Scientific Computing: In fields like physics and engineering, numerical simulations frequently involve calculations involving powers of two, especially when working with binary data.
Frequently Asked Questions (FAQ)
Q1: Why are powers of two so important in computing?
A1: Powers of two align perfectly with the binary number system (base-2), which is the foundation of digital computing. The binary system uses only two digits (0 and 1), representing the on/off states of transistors. This makes data processing and storage remarkably efficient.
Q2: Are kilobytes always exactly 1024 bytes?
A2: While traditionally kilobytes were defined as 1024 bytes, the International System of Units (SI) defines kilo as 1000. To avoid confusion, the term "kibibyte" (KiB) is now often used to represent 1024 bytes, while "kilobyte" (KB) represents 1000 bytes. However, in many practical contexts, especially within computing, 1024 bytes continues to be used as a kilobyte.
Q3: Can this calculation be done using other bases besides base-10?
A3: Yes, absolutely. The calculation can be performed in any base, though the process might appear different. However, the fundamental principle of division remains the same. Expressing the numbers in binary (base-2) would particularly simplify the calculation, given that both 1024 and 32 are easily represented in binary.
Q4: What if the numbers weren't powers of two? How would the calculation differ?
A4: If the numbers weren't powers of two, the simplification using exponents wouldn't be possible. Long division or a calculator would then be the most straightforward methods. The core principle of division, however, remains unchanged.
Q5: What are some other examples of problems that involve similar calculations?
A5: Numerous problems in computer science and mathematics involve similar calculations with powers of two. For example, calculating the number of bits needed to represent a specific number, determining memory requirements for data structures, or calculating the number of elements in a binary tree are all examples that involve similar mathematical reasoning and manipulation of powers of two.
Conclusion: A Foundation for Further Learning
The seemingly simple division problem, 1024 divided by 32, serves as a gateway to understanding fundamental concepts in computing and mathematics. Its solution (32) is not merely a numerical answer but a key to understanding the structure and organization of data within computer systems. By exploring different methods of calculation and understanding the significance of powers of two, we gain a deeper appreciation for the underlying principles that shape the digital world around us. This knowledge forms a solid foundation for further exploration into more advanced topics in computer science, mathematics, and related fields. From memory management to data transfer rates, this seemingly basic calculation plays a crucial role in countless technological applications.
Latest Posts
Latest Posts
-
15 Percent As A Decimal
Sep 18, 2025
-
Is 2 3 More Than 3 4
Sep 18, 2025
-
Normal Boiling Point Of Ethanol
Sep 18, 2025
-
Animals Live In The Pond
Sep 18, 2025
-
Which Elements Have Expanded Octets
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 024 Divided By 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.