15 Percent As A Decimal
thesills
Sep 18, 2025 · 5 min read
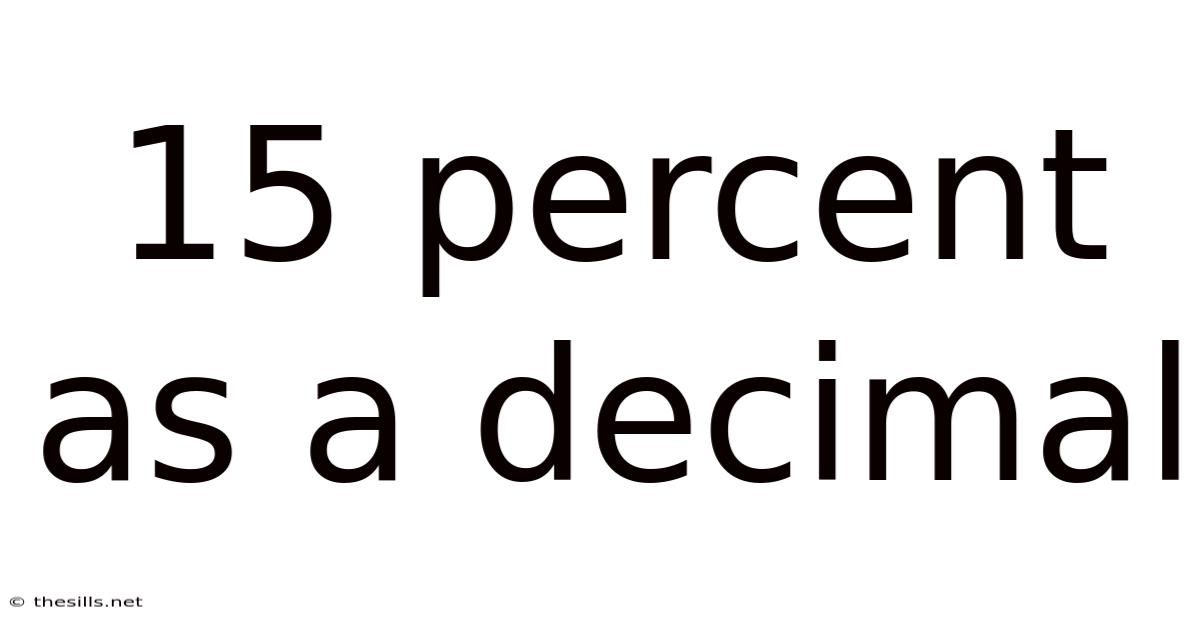
Table of Contents
15 Percent as a Decimal: A Comprehensive Guide
Understanding percentages is a fundamental skill in math and everyday life. Whether you're calculating discounts, taxes, or interest rates, converting percentages to decimals is a crucial step. This comprehensive guide will explore the concept of 15 percent as a decimal, providing a detailed explanation with practical examples and addressing frequently asked questions. We will delve into the underlying principles, explore various applications, and equip you with the knowledge to confidently handle percentage conversions in any context.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" – per cent from Latin. Therefore, 15 percent (15%) means 15 out of 100. This representation is particularly useful for comparing proportions and expressing relative values.
Converting Percentages to Decimals
Converting a percentage to a decimal involves dividing the percentage by 100. This is because a decimal represents a fraction where the denominator is a power of 10. For example, 0.15 is equivalent to 15/100.
To convert 15% to a decimal, we follow this simple step:
15% ÷ 100 = 0.15
Therefore, 15% as a decimal is 0.15. This is a crucial conversion to remember for various calculations.
Practical Applications of 15% as a Decimal
The decimal equivalent of 15% (0.15) finds numerous applications in various fields:
-
Calculating Sales Tax: If the sales tax in your region is 15%, you can easily calculate the tax amount on a purchase by multiplying the price by 0.15. For instance, a $100 item would have a sales tax of $100 * 0.15 = $15.
-
Determining Discounts: A 15% discount on an item can be calculated by multiplying the original price by 0.15, and then subtracting that amount from the original price. For a $50 item, the discount would be $50 * 0.15 = $7.50, resulting in a final price of $50 - $7.50 = $42.50. Alternatively, you can directly calculate the final price by multiplying the original price by (1 - 0.15) = 0.85. This is equivalent to calculating 85% of the original price.
-
Calculating Interest: If your savings account earns an annual interest rate of 15%, you can calculate the yearly interest by multiplying your principal amount by 0.15. For instance, $1000 invested at 15% interest would earn $1000 * 0.15 = $150 in one year (assuming simple interest). For compound interest, the calculation is more complex, but the decimal representation of the interest rate (0.15) remains essential.
-
Analyzing Data: In statistical analysis, percentages are frequently used to represent proportions. Converting to decimals facilitates calculations and comparisons. For instance, if 15% of a sample population exhibits a certain characteristic, this can be represented as 0.15 for easier statistical computations.
-
Financial Modeling: In finance, 15% could represent a growth rate, discount rate, or any other percentage-based parameter. Using the decimal equivalent (0.15) simplifies financial models and calculations.
Working with Fractions and Percentages: A Deeper Dive
Understanding the relationship between fractions, decimals, and percentages is crucial for mastering these concepts. Remember that a percentage is simply a fraction with a denominator of 100. We can express 15% as:
- Fraction: 15/100 (This can be simplified to 3/20)
- Decimal: 0.15
To convert a fraction to a percentage, multiply the fraction by 100. To convert a decimal to a percentage, multiply the decimal by 100 and add the % symbol.
Illustrative Examples: Beyond Simple Calculations
Let's explore more complex scenarios where converting 15% to 0.15 proves invaluable:
Example 1: Compound Interest Calculation
Suppose you invest $5,000 in an account that earns 15% interest compounded annually. To determine the value after 3 years, you would use the compound interest formula:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
In this case:
- P = $5,000
- r = 0.15 (15% as a decimal)
- n = 1 (compounded annually)
- t = 3
A = 5000 (1 + 0.15/1)^(1*3) = 5000 (1.15)^3 ≈ $7604.38
The decimal representation of the interest rate (0.15) is essential for accurate calculation.
Example 2: Calculating Percentage Change
Imagine the price of a certain stock increased from $20 to $23. To determine the percentage increase, we use the formula:
Percentage Change = [(New Value - Old Value) / Old Value] * 100
Percentage Change = [(23 - 20) / 20] * 100 = 15%
The 15% increase can easily be expressed as a decimal (0.15) for further calculations.
Frequently Asked Questions (FAQs)
Q1: How do I convert a decimal back to a percentage?
To convert a decimal back to a percentage, multiply the decimal by 100 and add the "%" symbol. For example, 0.15 * 100 = 15%, which is the same as our starting point.
Q2: What if I have a percentage with a decimal, like 15.5%?
Simply divide by 100 to convert to a decimal: 15.5% ÷ 100 = 0.155
Q3: Can I use a calculator for these conversions?
Yes! Most calculators have a percentage function or can easily perform the division by 100.
Q4: Why is converting to decimals important for calculations?
Converting percentages to decimals is crucial because most calculators and software programs perform calculations using decimals, not percentages. This allows for direct and accurate computation in various mathematical operations.
Q5: Are there any other ways to express 15%?
Yes, as mentioned previously, it can be expressed as the fraction 15/100 or its simplified form 3/20.
Conclusion
Understanding how to express 15% as a decimal (0.15) is a vital skill with far-reaching applications across numerous disciplines. From simple calculations like determining sales tax and discounts to more complex computations involving compound interest and financial modeling, the decimal representation of percentages simplifies calculations and improves accuracy. Mastering this conversion enhances your mathematical proficiency and practical problem-solving skills. By understanding the underlying principles and practicing the conversion process, you can confidently navigate percentage-based problems in your personal and professional life. The ability to seamlessly switch between percentages and decimals empowers you to analyze data, make informed decisions, and confidently handle a wide range of quantitative tasks. Remember, the key is consistent practice and understanding the fundamental connection between fractions, decimals, and percentages.
Latest Posts
Latest Posts
-
What Is Vander Waals Radius
Sep 18, 2025
-
103 Degrees F To C
Sep 18, 2025
-
18 Percent In Decimal Form
Sep 18, 2025
-
1 200 As A Decimal
Sep 18, 2025
-
Reaction Of Ester With Lialh4
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 15 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.