Is 2/3 More Than 3/4
thesills
Sep 18, 2025 · 5 min read
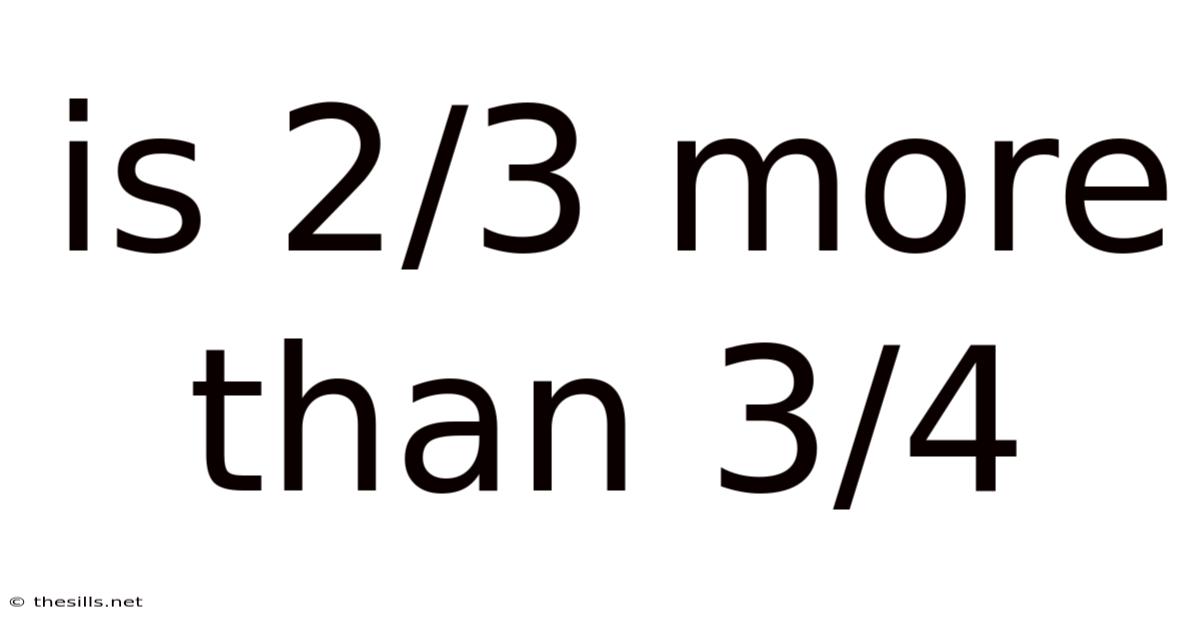
Table of Contents
Is 2/3 More Than 3/4? Understanding Fraction Comparison
This article delves into the seemingly simple yet fundamentally important question: is 2/3 more than 3/4? We'll explore various methods for comparing fractions, moving beyond simple intuition to develop a robust understanding of fractional arithmetic. This understanding is crucial for anyone working with fractions, from elementary school students to advanced mathematicians. We'll cover multiple approaches, ensuring you can confidently compare any two fractions.
Understanding Fractions: A Quick Review
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, in the fraction 2/3, the denominator (3) means the whole is divided into three equal parts, and the numerator (2) means we are considering two of those parts.
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. Once they have the same denominator, we can directly compare their numerators.
Let's apply this to our question: Is 2/3 more than 3/4?
-
Find the least common multiple (LCM) of the denominators: The denominators are 3 and 4. The LCM of 3 and 4 is 12.
-
Convert the fractions to equivalent fractions with the common denominator:
-
To convert 2/3 to a fraction with a denominator of 12, we multiply both the numerator and denominator by 4: (2 x 4) / (3 x 4) = 8/12
-
To convert 3/4 to a fraction with a denominator of 12, we multiply both the numerator and denominator by 3: (3 x 3) / (4 x 3) = 9/12
-
-
Compare the numerators: Now we compare 8/12 and 9/12. Since 8 < 9, we conclude that 8/12 < 9/12.
-
Therefore, 2/3 < 3/4. 2/3 is not more than 3/4; it is less.
Method 2: Converting to Decimals
Another effective method is to convert both fractions to decimals and then compare them. This method relies on our familiarity with decimal numbers and their ordering.
-
Convert 2/3 to a decimal: 2 ÷ 3 ≈ 0.6667 (repeating decimal)
-
Convert 3/4 to a decimal: 3 ÷ 4 = 0.75
-
Compare the decimals: Since 0.6667 < 0.75, we again conclude that 2/3 < 3/4.
Method 3: Visual Representation
Visualizing fractions can be incredibly helpful, especially for beginners. We can represent fractions using diagrams, such as circles or rectangles, divided into equal parts.
Imagine two identical circles. Divide the first circle into three equal parts and shade two of them (representing 2/3). Divide the second circle into four equal parts and shade three of them (representing 3/4). By visually comparing the shaded areas, it becomes clear that the shaded area in the second circle (3/4) is larger than the shaded area in the first circle (2/3).
Method 4: Cross-Multiplication
Cross-multiplication provides a quick and efficient method for comparing fractions. This method is particularly useful when dealing with larger or more complex fractions.
-
Cross-multiply the numerators and denominators:
-
Multiply the numerator of the first fraction (2) by the denominator of the second fraction (4): 2 x 4 = 8
-
Multiply the numerator of the second fraction (3) by the denominator of the first fraction (3): 3 x 3 = 9
-
-
Compare the products: Since 8 < 9, we conclude that 2/3 < 3/4.
This method is based on the principle that if a/b and c/d are two fractions, then a/b < c/d if and only if ad < bc.
Understanding the Magnitude of the Difference
While we've established that 2/3 is less than 3/4, it's also important to understand the magnitude of the difference. The difference between 3/4 and 2/3 is:
3/4 - 2/3 = (9/12) - (8/12) = 1/12
This means that 3/4 is 1/12 larger than 2/3. While seemingly small, this difference can be significant depending on the context.
Applications and Real-World Examples
The ability to compare fractions is crucial in numerous real-world applications:
-
Cooking and Baking: Recipes often require precise measurements using fractions of cups or other units. Understanding fraction comparison is essential for accurately scaling recipes up or down.
-
Construction and Engineering: Precise measurements are critical in these fields. Fractions are frequently used to represent dimensions and tolerances.
-
Finance and Accounting: Fractions are used extensively in calculations involving percentages, interest rates, and proportions.
-
Data Analysis: Understanding fractions and proportions is vital for interpreting data and making informed decisions based on statistical information.
Frequently Asked Questions (FAQ)
Q: What if the fractions have different denominators and finding the LCM is difficult?
A: You can still use cross-multiplication or convert the fractions to decimals. These methods work regardless of the complexity of the denominators.
Q: Are there any other methods for comparing fractions?
A: Yes, you can also use a calculator to convert the fractions to decimals and then compare them. You could also use visual aids like fraction bars or number lines.
Q: Why is finding a common denominator important?
A: Finding a common denominator allows us to directly compare the numerators, simplifying the comparison process. It’s the most intuitive method for many learners.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill in mathematics with far-reaching applications. We've explored several reliable methods—finding a common denominator, converting to decimals, visual representation, and cross-multiplication—to determine whether 2/3 is more than 3/4. We’ve definitively shown that 2/3 is less than 3/4. The key takeaway is not just the answer but the understanding of the different approaches and their applicability in various situations. Mastering these methods will equip you with the confidence to tackle any fraction comparison problem effectively. Remember to practice regularly to reinforce your understanding and build your skills. By understanding the underlying principles and applying the techniques explained above, you will become proficient in comparing fractions and confidently navigate the world of numerical calculations.
Latest Posts
Latest Posts
-
103 Degrees F To C
Sep 18, 2025
-
18 Percent In Decimal Form
Sep 18, 2025
-
1 200 As A Decimal
Sep 18, 2025
-
Reaction Of Ester With Lialh4
Sep 18, 2025
-
21 4 As A Mixed Number
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 More Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.