X 2 X 5 Simplify
thesills
Sep 18, 2025 · 6 min read
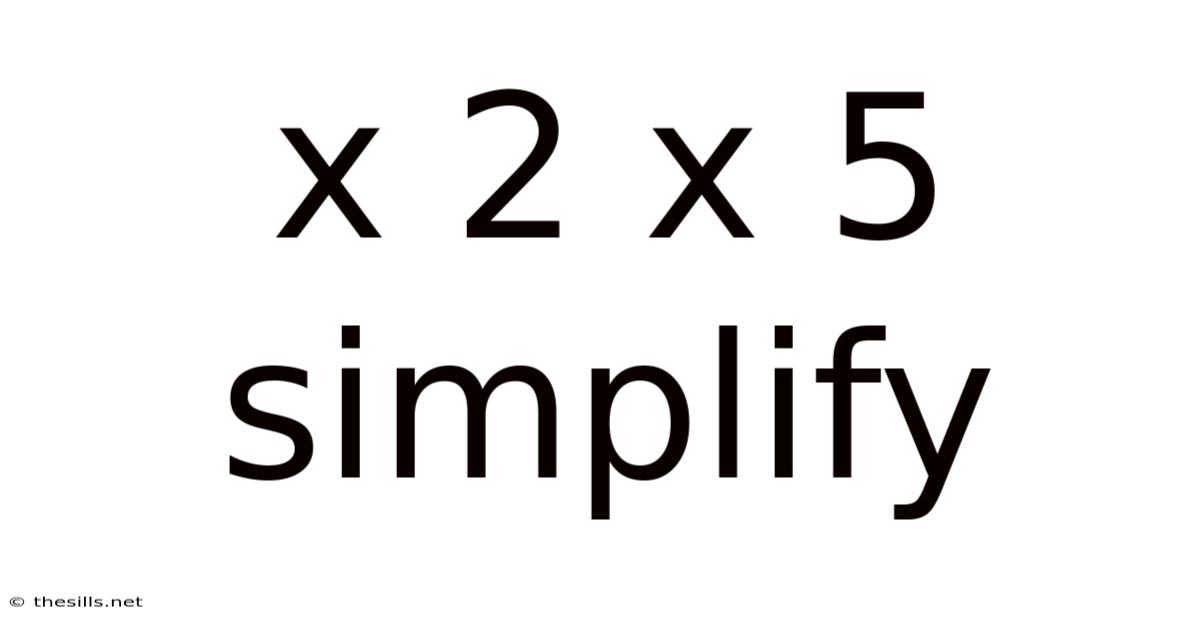
Table of Contents
Mastering Simplification: A Deep Dive into x² x 5
This article provides a comprehensive guide to simplifying the algebraic expression x² x 5, exploring its fundamentals, practical applications, and related concepts. We'll move beyond the basic simplification to understand the underlying principles of algebraic manipulation, making this a valuable resource for students and anyone looking to strengthen their understanding of algebra. We'll cover everything from the initial steps to advanced applications and frequently asked questions, ensuring a thorough understanding of this seemingly simple yet crucial algebraic concept.
Introduction: Understanding the Basics of Algebraic Simplification
Simplifying algebraic expressions is a fundamental skill in mathematics. It involves manipulating expressions to make them easier to understand and work with. This often involves combining like terms, using the distributive property, and applying the rules of exponents. The expression x² x 5 presents a straightforward yet important example that allows us to illustrate these key principles. Understanding how to simplify this expression will build a strong foundation for more complex algebraic manipulations.
Step-by-Step Simplification of x² x 5
The simplification of x² x 5 relies on the commutative and associative properties of multiplication. These properties allow us to rearrange and group terms without changing the overall value of the expression. Let’s break down the process step-by-step:
-
Identify the terms: We have two terms: x² and 5.
-
Recognize the commutative property: The commutative property of multiplication states that the order of factors does not affect the product (a x b = b x a). This means we can rearrange our expression as 5 x x².
-
Apply the associative property: The associative property of multiplication states that the grouping of factors does not affect the product (a x (b x c) = (a x b) x c). This allows us to group the numerical coefficient (5) with the variable term (x²).
-
Combine the terms: Since we are multiplying 5 and x², we simply write it as 5x². There is no addition or subtraction involved, so we cannot combine these terms further.
Therefore, the simplified form of x² x 5 is 5x².
The Significance of Coefficients and Variables
Let's delve deeper into the components of our simplified expression, 5x².
-
Coefficient: The number 5 is the coefficient. It's a numerical factor that multiplies the variable term. The coefficient indicates how many times the variable term is being added to itself. In our case, 5x² means x² + x² + x² + x² + x².
-
Variable: The letter x represents a variable, which can take on different numerical values. The exponent 2 indicates that the variable x is being multiplied by itself (x x x).
Understanding the roles of coefficients and variables is crucial in algebraic manipulation. It allows us to identify like terms and perform operations accurately.
Extending the Concept: More Complex Examples
While x² x 5 is a relatively simple expression, the principles used to simplify it apply to more complex scenarios. Let's consider some examples:
-
Example 1: 3x³ x 4y: This expression involves multiple variables. We can simplify it by multiplying the coefficients and combining the variable terms: 3 x 4 x x³ x y = 12x³y.
-
Example 2: (2x²)² x 3: This example introduces exponents of exponents. We need to address the exponent outside the parenthesis first: (2x²)² = 4x⁴. Then, we multiply this by 3: 4x⁴ x 3 = 12x⁴.
-
Example 3: 2x(x + 5): This example involves the distributive property. We multiply 2x by each term within the parenthesis: 2x(x) + 2x(5) = 2x² + 10x. Notice that we cannot simplify this further because 2x² and 10x are unlike terms (they have different powers of x).
These examples illustrate that the fundamental principles of simplification, such as the commutative, associative properties, and the distributive property remain crucial in solving more complex expressions.
The Importance of Order of Operations (PEMDAS/BODMAS)
When dealing with more intricate expressions, remember the order of operations, often represented by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). These mnemonics ensure consistency in evaluating expressions. Always address parentheses and exponents before multiplication, division, addition, and subtraction.
Explanation Through Visual Representation
Visualizing algebraic expressions can enhance understanding. Consider the expression x² x 5. We can visualize x² as a square with sides of length x. Multiplying this by 5 means we have five of these squares. This visual representation helps to understand that the result is five times the area of a square with side x, leading to the simplified form 5x².
Applications of Simplification in Real-World Problems
Simplifying algebraic expressions is not just a theoretical exercise. It has numerous practical applications across various fields:
-
Physics: Many physics equations involve algebraic expressions. Simplifying these expressions makes calculations easier and allows for a better understanding of the relationships between different variables.
-
Engineering: Engineers use algebraic expressions to model and analyze systems. Simplifying these expressions helps in designing efficient and reliable systems.
-
Economics: Economic models often rely on algebraic expressions to represent relationships between economic variables. Simplification helps in analyzing these models and making predictions.
-
Computer Science: Simplifying algebraic expressions is essential in algorithm optimization and improving the efficiency of computer programs.
Frequently Asked Questions (FAQ)
Q1: What happens if we have an expression like x² + 5?
A1: In this case, we cannot simplify the expression further because x² and 5 are unlike terms. They cannot be combined through addition.
Q2: Can we simplify x² x x³?
A2: Yes, this involves the rules of exponents. When multiplying terms with the same base (x), we add the exponents: x² x x³ = x⁽²⁺³⁾ = x⁵.
Q3: What if the expression is more complicated, for example, 2x²y + 3xy² - x²y?
A3: This involves combining like terms. We can combine 2x²y and -x²y: 2x²y - x²y = x²y. The expression simplifies to x²y + 3xy².
Q4: Is there a difference between x² x 5 and 5 x x²?
A4: No, due to the commutative property of multiplication, x² x 5 and 5 x x² are equivalent. The order of the terms does not change the result.
Conclusion: Mastering the Fundamentals
Simplifying algebraic expressions like x² x 5 may seem straightforward, but mastering this fundamental skill is crucial for success in advanced mathematics and its applications. Understanding the commutative and associative properties, the role of coefficients and variables, and the order of operations forms the bedrock of more complex algebraic manipulations. By practicing different types of simplification problems and understanding the underlying principles, you'll not only improve your mathematical skills but also gain a deeper appreciation for the elegance and power of algebra. The ability to simplify complex expressions efficiently is a valuable tool applicable in many diverse fields. Continue practicing, explore more complex expressions, and enjoy the journey of mathematical discovery!
Latest Posts
Latest Posts
-
Standard Enthalpy Of Formation Fe2o3
Sep 18, 2025
-
Integral X 1 X 4
Sep 18, 2025
-
27 Degrees Celsius To Kelvin
Sep 18, 2025
-
3 4 Of 240 Ml
Sep 18, 2025
-
3 Centre 2 Electron Bond
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 5 Simplify . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.