Integral X 1 X 4
thesills
Sep 18, 2025 · 5 min read
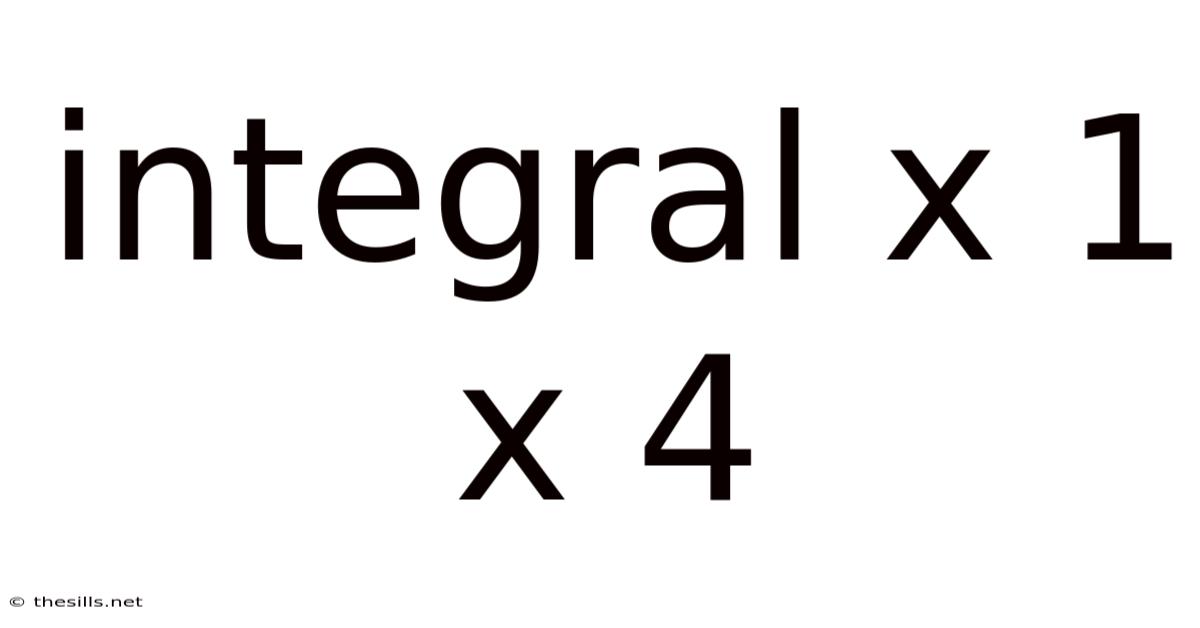
Table of Contents
Understanding and Solving the Definite Integral of x from 1 to 4
This article delves into the process of solving the definite integral of x from 1 to 4, a fundamental concept in calculus. We'll explore the underlying principles, provide a step-by-step solution, and address common questions surrounding definite integrals. Understanding this seemingly simple integral lays the groundwork for tackling more complex integration problems. This comprehensive guide will equip you with the knowledge and confidence to approach similar problems with ease.
Introduction: What is a Definite Integral?
In calculus, an integral represents the area under a curve. A definite integral, unlike an indefinite integral, calculates the area under a curve between two specified points, called the limits of integration. In our case, we're interested in finding the area under the curve of the function f(x) = x, specifically between the points x = 1 and x = 4. This is mathematically represented as:
∫¹⁴ x dx
The symbol ∫ denotes integration, 'x' is the function we're integrating, and 'dx' indicates that we're integrating with respect to x. The numbers 1 and 4 are the lower and upper limits of integration, respectively.
Step-by-Step Solution: Calculating the Definite Integral
Solving the definite integral involves two main steps: finding the antiderivative and evaluating it at the limits of integration.
1. Finding the Antiderivative:
The antiderivative (also known as the indefinite integral) is the reverse process of differentiation. If the derivative of a function F(x) is f(x), then F(x) is the antiderivative of f(x). In our case, f(x) = x. We need to find a function whose derivative is x.
The power rule of integration states: ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C, where 'n' is any real number except -1, and 'C' is the constant of integration.
Applying the power rule to our function f(x) = x (which is x¹):
∫x dx = (x¹⁺¹)/(1+1) + C = (x²)/2 + C
Therefore, the antiderivative of x is (x²)/2 + C. The constant of integration, C, is crucial for indefinite integrals, but it cancels out when evaluating definite integrals.
2. Evaluating the Antiderivative at the Limits of Integration:
Once we have the antiderivative, we evaluate it at the upper and lower limits of integration and subtract the results. This process is represented as:
[F(x)]¹⁴ = F(4) - F(1)
where F(x) = (x²)/2.
Let's substitute the limits:
F(4) = (4²)/2 = 16/2 = 8 F(1) = (1²)/2 = 1/2
Now, subtract F(1) from F(4):
F(4) - F(1) = 8 - (1/2) = 15/2 = 7.5
Therefore, the definite integral of x from 1 to 4 is 7.5. This means the area under the curve of y = x, between x = 1 and x = 4, is 7.5 square units.
Graphical Representation: Visualizing the Area
It’s helpful to visualize what we've calculated. The function y = x represents a straight line passing through the origin with a slope of 1. The definite integral calculates the area of a trapezoid bounded by this line, the x-axis, and the vertical lines x = 1 and x = 4. The area of this trapezoid is indeed 7.5 square units. This visual representation reinforces the meaning of the definite integral.
The Fundamental Theorem of Calculus: The Underlying Principle
The solution above hinges on the Fundamental Theorem of Calculus, a cornerstone of calculus. This theorem establishes a link between differentiation and integration, stating that differentiation and integration are inverse operations. It provides a powerful method for calculating definite integrals. The theorem formally states that if F(x) is an antiderivative of f(x), then:
∫ₐᵇ f(x) dx = F(b) - F(a)
This is precisely the method we used to solve our definite integral.
Applications of Definite Integrals: Real-World Relevance
Definite integrals have numerous applications across various fields:
- Physics: Calculating displacement from velocity, work done by a force, and center of mass.
- Engineering: Determining areas of irregular shapes, volumes of solids of revolution, and moments of inertia.
- Economics: Computing consumer surplus and producer surplus.
- Statistics: Calculating probabilities and expected values.
Solving Similar Problems: Expanding Your Understanding
Let's consider a slightly more complex example to further solidify your understanding. Suppose we want to calculate the definite integral:
∫₀³ (2x + 1) dx
1. Find the antiderivative:
∫(2x + 1) dx = ∫2x dx + ∫1 dx = x² + x + C
2. Evaluate at the limits of integration:
[(x² + x)]₀³ = (3² + 3) - (0² + 0) = 12
Therefore, the definite integral of (2x + 1) from 0 to 3 is 12.
Frequently Asked Questions (FAQ)
Q1: What if the function is negative within the integration interval?
A1: The definite integral will still give the net signed area. If the function is negative over a portion of the interval, the integral will be negative for that portion. The total value of the definite integral represents the algebraic sum of positive and negative areas.
Q2: What happens if the limits of integration are reversed?
A2: Reversing the limits of integration changes the sign of the definite integral. ∫ₐᵇ f(x) dx = -∫ᵇₐ f(x) dx.
Q3: Can I use numerical methods to approximate a definite integral?
A3: Yes, if an antiderivative is difficult or impossible to find analytically, numerical methods like the trapezoidal rule or Simpson's rule can approximate the definite integral. These methods involve dividing the area under the curve into smaller shapes and summing their areas.
Conclusion: Mastering Definite Integration
This comprehensive guide has walked you through the process of solving the definite integral of x from 1 to 4, explaining the underlying principles and providing a step-by-step solution. We've also explored the broader significance of definite integrals and their applications in various fields. By understanding these concepts, you've laid a strong foundation for tackling more advanced problems in calculus and related disciplines. Remember, practice is key to mastering integration. Work through various examples, and don't hesitate to explore additional resources to deepen your understanding. The journey of learning calculus is rewarding, and with persistence, you can achieve mastery in this essential field of mathematics.
Latest Posts
Latest Posts
-
Are Protons Bigger Than Neutrons
Sep 18, 2025
-
Number Of Electrons In Silver
Sep 18, 2025
-
Lewis Dot Structure For Water
Sep 18, 2025
-
Who Discovered The Element Gold
Sep 18, 2025
-
1 024 Divided By 32
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Integral X 1 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.