X 2 X 2 1
thesills
Sep 12, 2025 · 6 min read
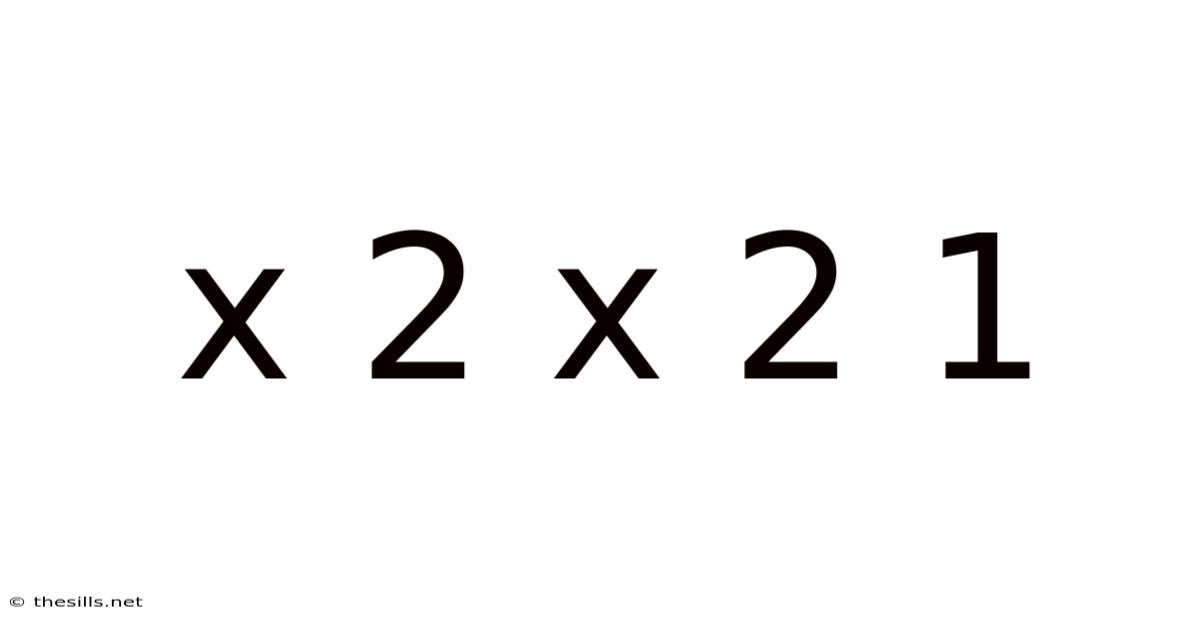
Table of Contents
Decoding the Mystery of "x 2 x 2 1": A Deep Dive into Combinatorics, Probability, and Problem-Solving
The seemingly simple sequence "x 2 x 2 1" might initially appear cryptic. However, this short string holds the key to understanding several fundamental mathematical concepts, particularly in the realms of combinatorics and probability. This article will explore various interpretations of this sequence, uncovering its hidden depths and revealing how it can be used to model and solve different types of problems. We'll delve into the possibilities, examine potential scenarios, and explore the underlying mathematical principles at play. This comprehensive guide will be accessible to both beginners and those with a stronger mathematical background, offering a journey into the fascinating world of pattern recognition and problem-solving.
Understanding the Potential Interpretations
The ambiguity of "x 2 x 2 1" is precisely what makes it so intriguing. The "x" acts as a wildcard, representing an unknown variable or element that can take on different values or meanings. This allows us to approach the sequence from multiple perspectives:
-
Algebraic Interpretation: We can view this sequence as a simplified algebraic expression, perhaps representing a series of operations. The "x" could be a variable, and the numbers represent coefficients or exponents. The challenge then becomes solving for "x" or determining the overall value of the expression.
-
Combinatorial Interpretation: The sequence could represent a combinatorial problem, where "x" represents a specific item or object, and the numbers reflect the number of times it appears or the constraints on its arrangement. This opens the door to exploring permutations and combinations.
-
Probabilistic Interpretation: The numbers could represent probabilities or frequencies of events. The "x" might represent an uncertain outcome or an unknown probability. This approach leads to questions about expected values and probability distributions.
-
Coding or Cryptography: In a more abstract sense, the sequence could be part of a code or cipher. The "x" might be a placeholder for a specific character or symbol within a larger code system.
Algebraic Explorations of "x 2 x 2 1"
Let's begin with the algebraic interpretation. The simplest approach would be to treat the sequence as a potential equation. However, without additional information or context, it’s impossible to solve for "x" directly. We need further constraints or a clear statement of the relationship between the elements. For example:
-
Scenario 1: x 2 x 2 1 = 0 This would create a simple equation where we could attempt to solve for "x." However, even with this constraint, the value of "x" is not immediately obvious. We'd need to manipulate the equation (perhaps by factoring or using the quadratic formula) to find potential solutions.
-
Scenario 2: x 2 x 2 1 = k (where k is a constant). This expands the possibilities considerably. The value of "k" would significantly impact the solution for "x".
-
Scenario 3: Consideration of Operations: The sequence could represent a series of operations. For example, it could be interpreted as: (x * 2) * (x * 2) + 1. This gives a quadratic equation that can be solved for x given a specific value for the overall expression.
Combinatorial Possibilities and Permutations
If we view "x 2 x 2 1" through a combinatorial lens, the sequence takes on a different meaning. The "x" could represent a unique object, and the numbers represent the quantity or frequency of each element within a set. For example:
-
Scenario 1: Arrangements: If we have a set of objects containing one "x," two "2"s, and two "1"s, we can explore the different ways to arrange these objects. This is a classic permutation problem where the order matters. The number of unique arrangements can be calculated using factorial notation and considering repetitions.
-
Scenario 2: Subsets: Alternatively, we could focus on subsets. How many different subsets can we create from this set of objects? This is a different type of combinatorial problem, focusing on the selection of elements rather than their arrangement.
-
Scenario 3: Constraints and Conditions: Adding constraints, such as requiring the "x" to always be placed first, or specifying that no two "1"s can be adjacent, drastically alters the number of possible combinations and requires more sophisticated combinatorial techniques to solve.
Probabilistic Explorations of "x 2 x 2 1"
From a probabilistic viewpoint, "x 2 x 2 1" can represent probabilities or frequencies of events. "x" might represent the probability of an unknown event. Depending on the context, we might be interested in:
-
Scenario 1: Expected Value: If the numbers represent the outcomes of a random variable, we can calculate the expected value. This is the average outcome we would expect over many repetitions of the experiment.
-
Scenario 2: Probability Distribution: We could model the sequence as a probability distribution, mapping the numerical values to their corresponding probabilities. This would require defining a probability mass function (PMF) or a probability density function (PDF), depending on whether the variables are discrete or continuous.
-
Scenario 3: Conditional Probabilities: The sequence might represent conditional probabilities. For example, "2 x 2" might represent the probability of event A occurring given that event B has occurred.
Advanced Applications and Further Considerations
The analysis of "x 2 x 2 1" extends beyond the basic interpretations discussed above. More complex scenarios could involve:
-
Recursive Relationships: The sequence could be part of a recursive formula or algorithm, where the value of "x" at one step influences the value in subsequent steps.
-
Matrix Representations: The sequence could be represented as a matrix, potentially leading to linear algebra problems.
-
Game Theory: In game theory, the sequence could describe strategic choices or payoffs in a game.
-
Graph Theory: The numbers could represent nodes and edges in a graph, with "x" playing a role in defining the graph's structure or properties.
Frequently Asked Questions (FAQ)
Q: What is the single definitive solution to "x 2 x 2 1"?
A: There is no single definitive solution without additional context or constraints. The meaning and solution depend entirely on the interpretation and the rules of the system in which the sequence is presented.
Q: Can "x" represent any value?
A: In some interpretations, yes. In others, constraints or conditions might limit the possible values of "x." For example, in a combinatorial problem, "x" might represent a specific object from a defined set.
Q: What mathematical concepts are most relevant to understanding "x 2 x 2 1"?
A: Combinatorics, probability, algebra, and potentially even aspects of graph theory or linear algebra, depending on the interpretation.
Q: How can I learn more about solving problems like this?
A: Studying combinatorics and probability will provide a strong foundation for tackling these types of problems. Textbooks and online courses on these subjects offer in-depth explanations and practice problems.
Conclusion: Unveiling the Power of Ambiguity
The seemingly simple sequence "x 2 x 2 1" serves as a powerful reminder of the multifaceted nature of mathematics and the importance of clearly defining the context and constraints of a problem before attempting a solution. Its ambiguity allows for diverse interpretations and problem-solving approaches, highlighting the interconnectedness of various mathematical fields. While there's no singular answer, the exploration itself reveals the richness and depth of mathematical reasoning and encourages a deeper understanding of combinatorics, probability, and the power of flexible thinking. By approaching such open-ended problems with creativity and a systematic approach, we uncover a wealth of possibilities and develop valuable problem-solving skills applicable across numerous fields.
Latest Posts
Latest Posts
-
X 3 2x 2 3x
Sep 12, 2025
-
Which Soil Is The Stickiest
Sep 12, 2025
-
Differentiate Between Thalamus And Hypothalamus
Sep 12, 2025
-
Longest Platform In The World
Sep 12, 2025
-
Where Are Electrical Synapses Found
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.