X 3 2x 2 3x
thesills
Sep 12, 2025 · 6 min read
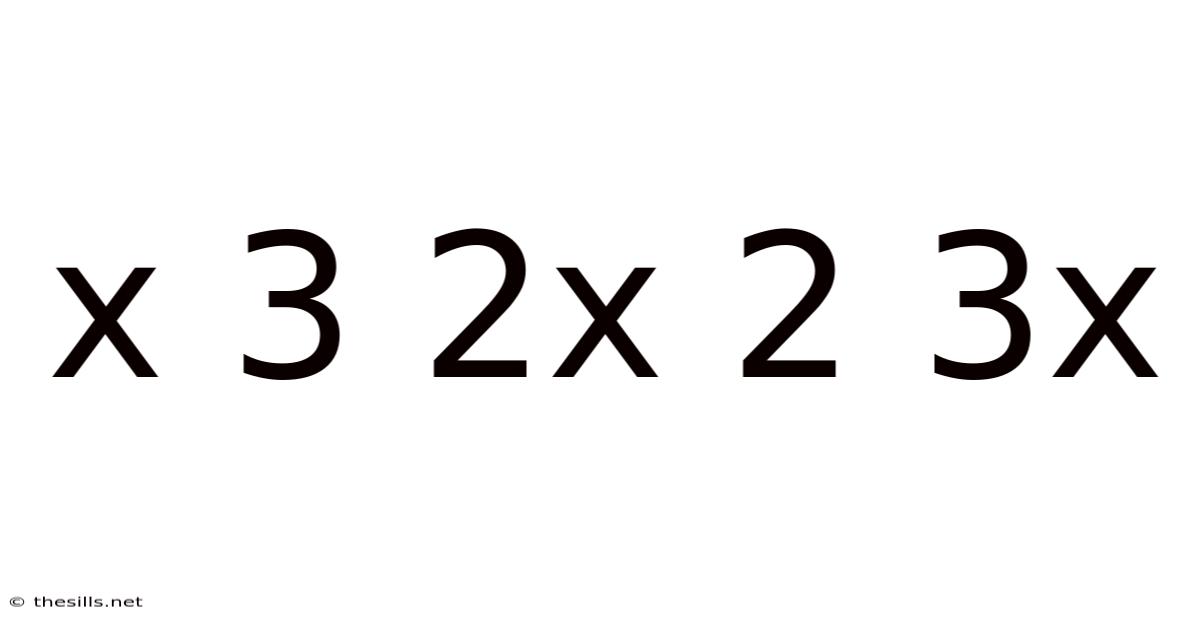
Table of Contents
Decoding the Mystery: Exploring the Mathematical Expressions x³ + 2x² + 3x
This article delves into the mathematical expression x³ + 2x² + 3x, exploring its components, potential applications, and methods for manipulation. We'll uncover its secrets, demystifying the seemingly simple equation and revealing its underlying complexities and power. Understanding this expression provides a foundational stepping stone to more advanced algebraic concepts and problem-solving techniques. This exploration will suit students, mathematicians, and anyone curious about the beauty and power of algebra.
Introduction: Understanding the Building Blocks
At first glance, x³ + 2x² + 3x might appear intimidating, but it's simply a polynomial expression. Let's break down each component:
- x³ (x cubed): This represents x multiplied by itself three times (x * x * x). The exponent 3 indicates the degree of this term.
- 2x² (2x squared): This term represents 2 multiplied by x multiplied by x. The coefficient 2 scales the value of x². The exponent 2 indicates its degree.
- 3x (3x): This is a linear term, meaning the exponent of x is 1 (often not explicitly written). The coefficient 3 scales the value of x.
The entire expression, x³ + 2x² + 3x, is a polynomial because it's a sum of terms, each involving a variable (x) raised to a non-negative integer power. Specifically, it's a cubic polynomial because the highest power of x is 3.
Factoring the Polynomial: Unveiling Hidden Structure
Factoring a polynomial means rewriting it as a product of simpler expressions. While not all polynomials can be easily factored, sometimes we can find common factors to simplify the expression. In this case, we can factor out an x:
x³ + 2x² + 3x = x(x² + 2x + 3)
This factored form reveals a hidden structure. The expression is now represented as the product of x and a quadratic expression (x² + 2x + 3). This factorization can be useful in various mathematical operations, as we'll see later.
Solving for x: Finding the Roots
Finding the roots or zeros of a polynomial means determining the values of x that make the expression equal to zero. This involves solving the equation:
x³ + 2x² + 3x = 0
Using the factored form, we can simplify this to:
x(x² + 2x + 3) = 0
This equation is satisfied if either x = 0 or x² + 2x + 3 = 0. The first solution is straightforward: x = 0.
To solve the quadratic equation x² + 2x + 3 = 0, we can use the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
where a = 1, b = 2, and c = 3. Substituting these values, we get:
x = [-2 ± √(2² - 4 * 1 * 3)] / 2 * 1 = [-2 ± √(-8)] / 2
Notice that we have a negative number under the square root. This means the roots are complex numbers, involving the imaginary unit i (where i² = -1). The solutions are:
x = -1 + i√2 and x = -1 - i√2
Therefore, the three roots of the cubic polynomial x³ + 2x² + 3x are 0, -1 + i√2, and -1 - i√2. The presence of complex roots highlights the richness and complexity that even seemingly simple polynomial equations can possess.
Graphing the Polynomial: Visualizing the Expression
Graphing the polynomial x³ + 2x² + 3x provides a visual representation of its behavior. The graph will be a curve that passes through the x-axis at the roots we calculated (0, in this case, the complex roots are not visible on the real number plane). The graph will show how the value of the expression changes as x varies. The positive leading coefficient (the coefficient of x³, which is 1) indicates that the graph will rise to the right and fall to the left.
The shape of the cubic curve is characteristic of a third-degree polynomial: it can have at most two turning points (where the curve changes direction from increasing to decreasing or vice versa). The exact location of these turning points can be determined through calculus, involving finding the derivative and setting it to zero.
Applications: Where Does This Expression Appear?
This seemingly simple polynomial, x³ + 2x² + 3x, may appear surprisingly often in various fields.
- Physics: It can represent simplified models of physical phenomena, such as the displacement of an object under certain forces or the rate of change of a quantity over time. The coefficients would then represent physical constants related to the specific system.
- Engineering: Polynomial expressions are fundamental in engineering design, especially when modeling curves, surfaces, and trajectories. This particular polynomial could be used as a component of a more complex model in areas like mechanical engineering or civil engineering.
- Economics: Polynomial functions can be used to model economic variables. This polynomial could potentially represent a simplified growth model or a cost function.
- Computer Science: In computer graphics, polynomials are used to define curves and surfaces. These polynomials are also essential in numerical analysis and approximation methods.
Further Explorations and Advanced Concepts
This introduction to x³ + 2x² + 3x can serve as a springboard to more advanced topics:
- Partial Fraction Decomposition: For more complex rational functions (fractions involving polynomials), partial fraction decomposition techniques can simplify integration and other mathematical operations.
- Numerical Methods: When analytical solutions are difficult or impossible to obtain, numerical methods such as Newton-Raphson iteration can approximate the roots of polynomials.
- Calculus: Studying the derivative and integral of this polynomial provides insights into its rate of change and accumulated value over an interval.
- Linear Algebra: Polynomials can be represented as vectors in certain vector spaces, leading to powerful analytical techniques.
Frequently Asked Questions (FAQ)
Q: Can this polynomial be factored further than x(x² + 2x + 3)?
A: No, the quadratic expression (x² + 2x + 3) cannot be factored further using real numbers. Its roots are complex, as shown earlier.
Q: What is the significance of the coefficients (1, 2, and 3)?
A: The coefficients scale the influence of each term in the polynomial. Changing the coefficients would alter the shape and position of the graph, as well as the values of the roots.
Q: How can I find the turning points of the graph?
A: You need to find the derivative of the polynomial, set it equal to zero, and solve for x. This will give you the x-coordinates of the turning points. Then substitute these x values back into the original polynomial to find the corresponding y-coordinates.
Q: Are there any real-world applications for this specific polynomial?
A: While this specific polynomial might not have a widely known, direct application, it's a building block and demonstrates fundamental concepts widely used in numerous applications in science, engineering, and economics. More complex polynomial models often incorporate simpler ones like this as part of their structure.
Conclusion: A Deeper Appreciation for Simplicity
The seemingly simple polynomial expression, x³ + 2x² + 3x, unveils a wealth of mathematical concepts and techniques. From factoring and solving for roots to graphing and understanding its applications, this exploration showcases the depth and richness of even fundamental algebraic concepts. By understanding this expression, we gain a foundational understanding that can be applied to more complex mathematical challenges across various fields. This journey emphasizes the beauty and power hidden within apparently straightforward mathematical expressions, encouraging further exploration and a deeper appreciation for the elegance of mathematics.
Latest Posts
Latest Posts
-
Diameter Of A Nitrogen Molecule
Sep 12, 2025
-
What Animals Have Big Ears
Sep 12, 2025
-
Functional Group Of Ethanoic Acid
Sep 12, 2025
-
What Is The Exponential Form
Sep 12, 2025
-
Sum Of Interior Angles Hexagon
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about X 3 2x 2 3x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.