X 2 Ax Bx Ab
thesills
Sep 13, 2025 · 6 min read
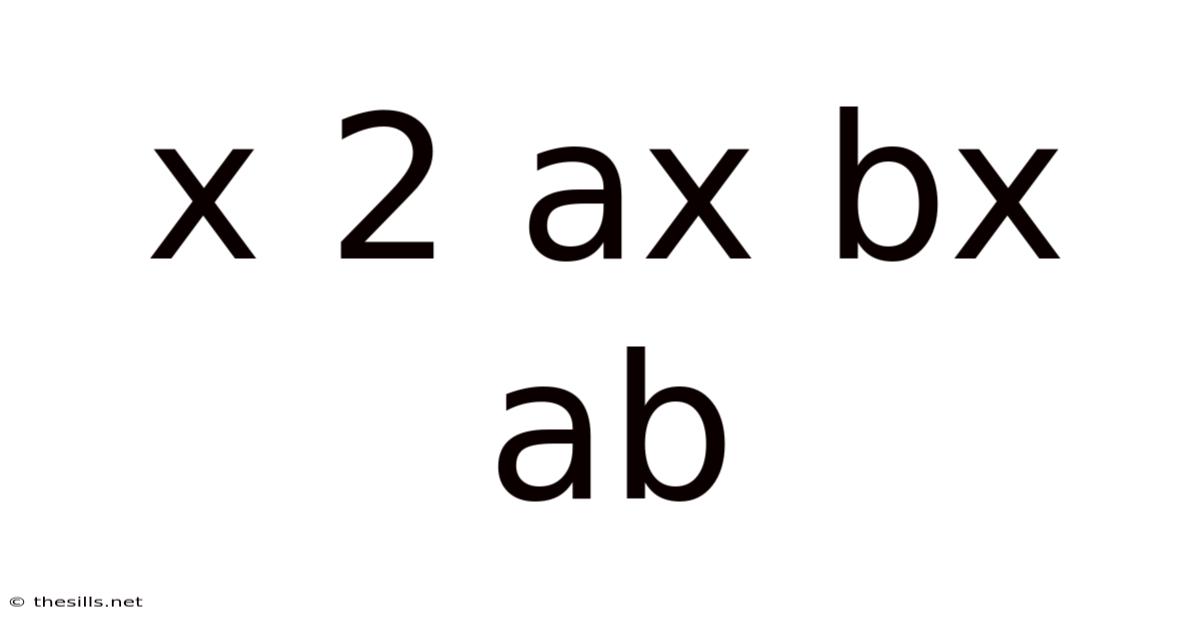
Table of Contents
Decoding the Quadratic: Exploring x² + ax + bx + ab
The expression x² + ax + bx + ab might seem intimidating at first glance, especially to those new to algebra. However, this seemingly complex algebraic expression is actually a gateway to understanding fundamental concepts in factoring, quadratic equations, and algebraic manipulation. This comprehensive guide will break down this expression step-by-step, exploring its various facets, providing illustrative examples, and addressing frequently asked questions. By the end, you'll not only understand how to factor this expression but also appreciate its broader significance in mathematics.
Understanding the Components
Before diving into the factorization process, let's dissect the individual components of the expression x² + ax + bx + ab:
-
x²: This represents the square of a variable x. It's a fundamental term in quadratic equations.
-
ax: This is a term where 'a' is a constant (a number) and is multiplied by the variable x. The value of 'a' can be positive, negative, or zero.
-
bx: Similar to the previous term, 'b' is another constant multiplied by x.
-
ab: This is the product of the two constants 'a' and 'b'. It’s a constant term without any variables.
The key to understanding and working with this expression lies in recognizing the pattern and applying appropriate factorization techniques.
Factoring the Expression: A Step-by-Step Approach
The most efficient way to factor x² + ax + bx + ab is through a process called factoring by grouping. This method involves grouping the terms strategically and then extracting common factors. Here’s a step-by-step guide:
Step 1: Grouping the Terms
The first step involves grouping the terms in pairs. We group the first two terms together and the last two terms together:
(x² + ax) + (bx + ab)
Step 2: Factoring Out Common Factors
Now, we look for common factors within each group. In the first group (x² + ax), the common factor is x. In the second group (bx + ab), the common factor is b. We factor these out:
x(x + a) + b(x + a)
Step 3: Identifying the Common Binomial Factor
Notice that both terms in the expression now share a common factor: (x + a). This is a binomial factor (a factor with two terms).
Step 4: Factoring Out the Common Binomial
We factor out the common binomial (x + a):
(x + a)(x + b)
This is the factored form of the expression x² + ax + bx + ab. This demonstrates that the expression is the expansion of the product of two binomials (x+a) and (x+b).
Illustrative Examples
Let's solidify our understanding with some numerical examples:
Example 1:
Factor the expression x² + 5x + 2x + 10
Following the steps above:
- Grouping: (x² + 5x) + (2x + 10)
- Factoring out common factors: x(x + 5) + 2(x + 5)
- Common binomial factor: (x + 5)
- Factoring out the common binomial: (x + 5)(x + 2)
Therefore, x² + 5x + 2x + 10 = (x + 5)(x + 2)
Example 2:
Factor the expression x² - 3x + 4x - 12
- Grouping: (x² - 3x) + (4x - 12)
- Factoring out common factors: x(x - 3) + 4(x - 3)
- Common binomial factor: (x - 3)
- Factoring out the common binomial: (x - 3)(x + 4)
Therefore, x² - 3x + 4x - 12 = (x - 3)(x + 4)
These examples highlight the versatility of the factoring by grouping method, applicable even when dealing with negative coefficients.
The Connection to Quadratic Equations
The expression x² + ax + bx + ab is intrinsically linked to quadratic equations. A quadratic equation is an equation of the form ax² + bx + c = 0, where a, b, and c are constants and a ≠ 0. Our expression, when set equal to zero, becomes a quadratic equation:
x² + ax + bx + ab = 0
By factoring the expression as we’ve learned, we can solve this quadratic equation. The solutions (or roots) are the values of x that make the equation true. In the factored form (x + a)(x + b) = 0, the solutions are x = -a and x = -b. This is because the product of two factors is zero only if at least one of the factors is zero.
Expanding the Understanding: Different Scenarios and Challenges
While the factoring by grouping method is highly effective for expressions in the form x² + ax + bx + ab, it's important to acknowledge that not all quadratic expressions will neatly fit this pattern. Let's explore some variations:
-
Expressions with a common factor: Sometimes, the entire expression might share a common factor before applying grouping. For example, 2x² + 4x + 6x + 12 can be simplified by first factoring out the common factor 2, resulting in 2(x² + 2x + 3x + 6), and then proceeding with grouping.
-
Expressions that don't factor easily: Not all quadratic expressions can be easily factored using integers. In such cases, other methods like the quadratic formula or completing the square are needed to find the solutions.
-
Expressions with more than four terms: Factoring by grouping can sometimes be extended to expressions with more than four terms, but it requires careful observation of common factors and strategic grouping.
The Significance of Factoring in Mathematics
Factoring is not just a procedural technique; it's a fundamental tool in algebra and beyond. It enables us to:
- Simplify expressions: Factoring simplifies complex expressions, making them easier to understand and manipulate.
- Solve equations: As demonstrated with quadratic equations, factoring is crucial in finding solutions to various types of equations.
- Analyze functions: Factoring helps in analyzing the behavior of functions, identifying roots, intercepts, and other key features.
- Solve real-world problems: Many real-world problems in various fields, including physics, engineering, and economics, involve solving quadratic equations and utilize factoring as a primary tool.
Frequently Asked Questions (FAQ)
Q1: What if the expression doesn't factor nicely?
A1: If the expression doesn't factor easily using integers, you'll need to employ other methods, such as the quadratic formula or completing the square, to find the roots or solutions.
Q2: Is there more than one way to factor x² + ax + bx + ab?
A2: While factoring by grouping is the most efficient method, in some cases, you might be able to rearrange the terms and still obtain the same factored form. However, the most common and recommended method is the one described above.
Q3: Why is factoring important in higher-level mathematics?
A3: Factoring is a foundational skill that underpins many advanced mathematical concepts, including calculus, linear algebra, and abstract algebra. The ability to manipulate and simplify expressions through factoring is crucial for success in these areas.
Q4: Can I use this method for expressions with higher powers of x?
A4: While factoring by grouping is most effective for quadratic expressions, the principle of identifying and extracting common factors remains applicable to expressions with higher powers of x, although the complexity increases significantly. More advanced techniques are often required.
Conclusion
The expression x² + ax + bx + ab, while initially appearing complex, reveals its elegance and power when approached methodically. Through factoring by grouping, we can readily simplify this expression and uncover its connection to quadratic equations and their solutions. Understanding this process is not merely about mastering a technique; it's about gaining a deeper insight into the fundamental principles of algebra and their application in a wide range of mathematical contexts. Mastering this skill unlocks a world of possibilities in solving problems and exploring the intricacies of mathematics. So, practice diligently, explore variations, and embrace the power of factoring!
Latest Posts
Latest Posts
-
All Equilateral Triangles Are Isosceles
Sep 13, 2025
-
How To Calculate Q Value
Sep 13, 2025
-
Factor 6x 2 5x 6
Sep 13, 2025
-
Roots Of A Complex Number
Sep 13, 2025
-
But 1 En 3 Yne
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about X 2 Ax Bx Ab . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.