Factor 6x 2 5x 6
thesills
Sep 13, 2025 · 6 min read
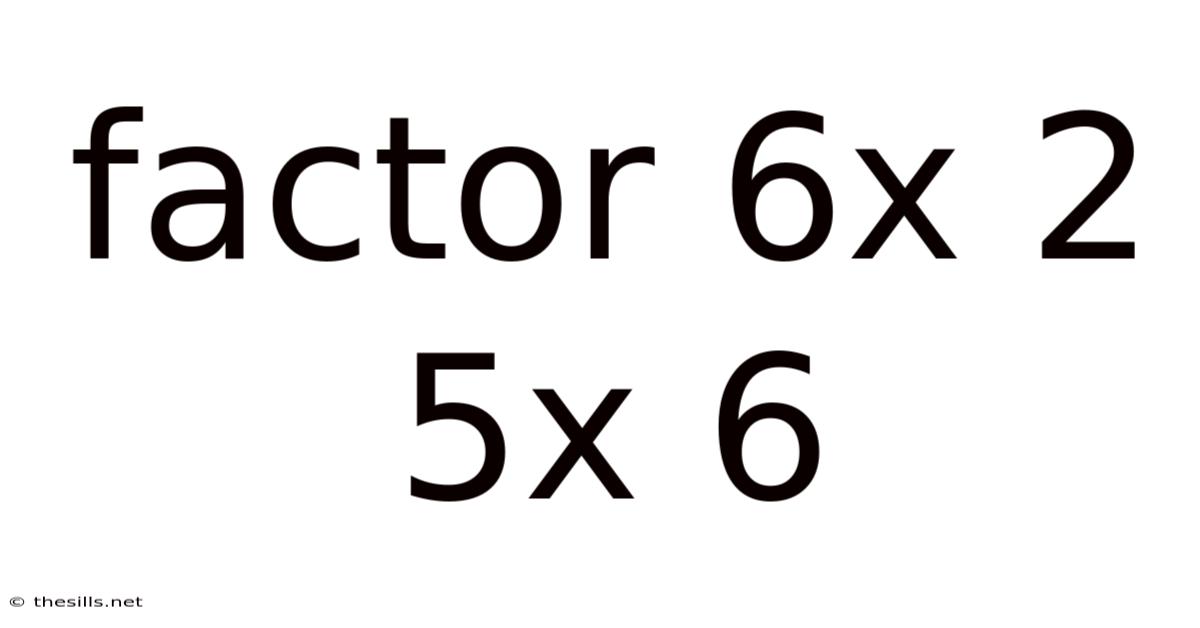
Table of Contents
Factoring the Quadratic Expression: 6x² + 5x - 6
This article will comprehensively explore the process of factoring the quadratic expression 6x² + 5x - 6. We will delve into various methods, explaining the underlying mathematical principles and providing a step-by-step guide suitable for students of various mathematical backgrounds. Understanding quadratic factoring is crucial for solving quadratic equations, simplifying algebraic expressions, and laying a solid foundation for more advanced mathematical concepts. By the end of this article, you'll be able to confidently factor similar quadratic expressions.
Understanding Quadratic Expressions
Before we tackle the factoring process, let's define what a quadratic expression is. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and a is not equal to zero. In our case, a = 6, b = 5, and c = -6.
Method 1: Factoring by Grouping (AC Method)
This method is a systematic approach to factoring trinomial quadratic expressions. It involves finding two numbers that add up to b and multiply to ac.
Steps:
-
Find the product ac: In our example, a = 6 and c = -6, so ac = 6 * (-6) = -36.
-
Find two numbers that add up to b and multiply to ac: We need two numbers that add up to 5 (our b value) and multiply to -36. These numbers are 9 and -4 (9 + (-4) = 5 and 9 * (-4) = -36).
-
Rewrite the middle term: Replace the middle term (5x) with the two numbers we found, keeping the expression equal: 6x² + 9x - 4x - 6.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
- 3x(2x + 3) - 2(2x + 3)
-
Factor out the common binomial: Notice that (2x + 3) is common to both terms. Factor it out: (2x + 3)(3x - 2).
Therefore, the factored form of 6x² + 5x - 6 is (2x + 3)(3x - 2).
Method 2: Trial and Error
This method involves a more intuitive approach, testing different combinations of factors until you find the correct one. It's faster once you gain experience, but it can be time-consuming for beginners.
Steps:
-
Factor the first term (6x²): The possible pairs of factors are (6x, x) and (3x, 2x).
-
Factor the last term (-6): The possible pairs of factors are (1, -6), (-1, 6), (2, -3), (-2, 3), (3, -2), (-3, 2), (6, -1), (-6, 1).
-
Test different combinations: We need to find a combination that, when multiplied and added together, results in the middle term (5x). Let's try some combinations:
- (6x + 1)(x - 6) This expands to 6x² - 35x - 6 (Incorrect)
- (6x - 1)(x + 6) This expands to 6x² + 35x - 6 (Incorrect)
- (3x + 2)(2x - 3) This expands to 6x² - 5x - 6 (Incorrect)
- (3x - 2)(2x + 3) This expands to 6x² + 5x - 6 (Correct!)
Therefore, the factored form is (3x - 2)(2x + 3). Note that the order of the factors doesn't matter; (3x - 2)(2x + 3) is equivalent to (2x + 3)(3x - 2).
Method 3: Using the Quadratic Formula (Indirect Factoring)
While not a direct factoring method, the quadratic formula can help find the roots of the quadratic equation (6x² + 5x - 6 = 0), which can then be used to construct the factored form.
The quadratic formula is: x = [-b ± √(b² - 4ac)] / 2a
Substituting our values (a = 6, b = 5, c = -6), we get:
x = [-5 ± √(5² - 4 * 6 * -6)] / (2 * 6) x = [-5 ± √(25 + 144)] / 12 x = [-5 ± √169] / 12 x = [-5 ± 13] / 12
This gives us two solutions:
x₁ = (-5 + 13) / 12 = 8 / 12 = 2/3 x₂ = (-5 - 13) / 12 = -18 / 12 = -3/2
These solutions represent the roots of the quadratic equation. To construct the factored form, we rewrite the roots as factors:
(x - 2/3) and (x + 3/2)
To eliminate the fractions, we multiply each factor by the denominator of the fraction:
3(x - 2/3) = 3x - 2 2(x + 3/2) = 2x + 3
Thus, the factored form is (3x - 2)(2x + 3).
A Deeper Dive into the Mathematics: Why These Methods Work
The success of these methods hinges on the fundamental theorem of algebra, which states that a polynomial of degree n has exactly n roots (possibly complex). In our case, we have a quadratic (degree 2), meaning it has two roots. Factoring essentially reverses the process of multiplying binomials.
Factoring by Grouping: This method leverages the distributive property of multiplication. By strategically rewriting the middle term, we create pairs of terms with common factors, allowing us to factor out these GCFs and reveal the underlying binomial factors.
Trial and Error: This method relies on understanding the distributive property and systematically testing combinations of factors until we find the ones that satisfy the equation.
Quadratic Formula: The quadratic formula is derived from completing the square, a technique used to solve quadratic equations. It provides a direct way to find the roots, which can then be used to construct the factored form. It is particularly useful when factoring by other methods is difficult or impossible.
Frequently Asked Questions (FAQ)
Q: What if I can't find the factors using trial and error?
A: If you're struggling with trial and error, the factoring by grouping (AC method) provides a more structured approach. The quadratic formula always provides the roots, even if factoring is challenging.
Q: Is there only one correct way to factor a quadratic expression?
A: No, the order of the factors doesn't matter. (3x - 2)(2x + 3) is equivalent to (2x + 3)(3x - 2).
Q: What if the quadratic expression cannot be factored using integers?
A: Some quadratic expressions cannot be factored using only integers. In such cases, the quadratic formula will still provide the roots, which can be used to express the factors, potentially involving irrational numbers or complex numbers.
Q: Can I use these methods for higher-degree polynomials?
A: The methods described here primarily apply to quadratic expressions (degree 2). Factoring higher-degree polynomials can be significantly more complex and often requires more advanced techniques.
Conclusion
Factoring the quadratic expression 6x² + 5x - 6 is achievable using various methods, including factoring by grouping, trial and error, and indirectly through the quadratic formula. Each method offers a different approach, catering to varying levels of mathematical proficiency. Understanding these methods and the underlying mathematical principles will equip you with the skills to tackle similar quadratic factoring problems and solidify your understanding of fundamental algebraic concepts. Remember to practice regularly to improve your speed and accuracy. The more you practice, the more intuitive and efficient the process will become. Mastering quadratic factoring is a significant step towards excelling in algebra and beyond.
Latest Posts
Latest Posts
-
Difference Between Kuchipudi And Bharatanatyam
Sep 13, 2025
-
Zinc Metal Nonmetal Or Metalloid
Sep 13, 2025
-
6x 2 5x 1 Factor
Sep 13, 2025
-
What Is A Complementary Strand
Sep 13, 2025
-
Where Are The Anticodons Located
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Factor 6x 2 5x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.