6x 2 5x 1 Factor
thesills
Sep 13, 2025 · 5 min read
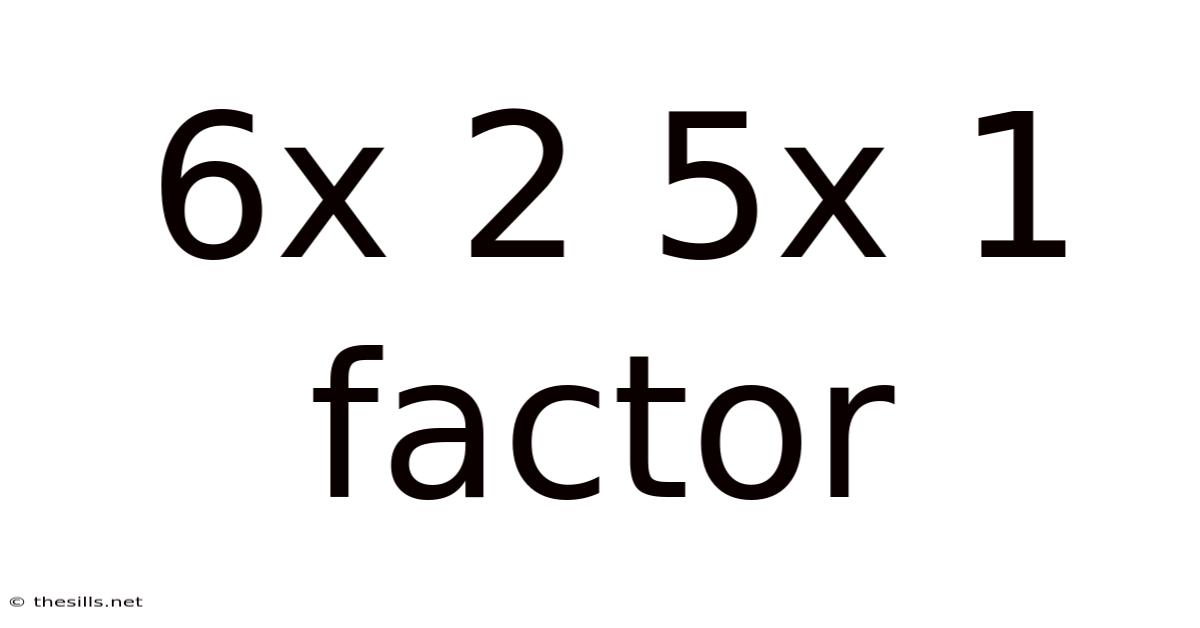
Table of Contents
Unveiling the Mysteries of 6x² + 5x + 1: Factoring Quadratic Expressions
Understanding how to factor quadratic expressions is a fundamental skill in algebra. This article will delve into the process of factoring the specific quadratic expression 6x² + 5x + 1, explaining the steps involved, the underlying mathematical principles, and offering strategies for tackling similar problems. We'll explore different methods, address common mistakes, and provide a solid foundation for mastering quadratic factoring.
Introduction: What is Factoring?
Factoring, in the context of algebra, involves expressing a mathematical expression as a product of simpler expressions. Think of it like reverse multiplication. For example, the factored form of 12 is 2 x 2 x 3. Similarly, factoring a quadratic expression like 6x² + 5x + 1 means finding two simpler expressions whose product equals the original expression. This skill is crucial for solving quadratic equations, simplifying expressions, and understanding various mathematical concepts. Mastering this process will unlock deeper comprehension of higher-level mathematics.
Method 1: The AC Method (for Factoring Trinomials)
This method is particularly useful for factoring trinomial quadratic expressions of the form ax² + bx + c, where a, b, and c are constants. Let's apply it to our example, 6x² + 5x + 1.
-
Identify a, b, and c: In our expression, a = 6, b = 5, and c = 1.
-
Find the product ac: Multiply a and c: 6 * 1 = 6.
-
Find two numbers that add up to b and multiply to ac: We need two numbers that add up to 5 (our b value) and multiply to 6 (our ac value). These numbers are 3 and 2. (3 + 2 = 5 and 3 * 2 = 6).
-
Rewrite the middle term: Rewrite the original expression, replacing the middle term (5x) with the two numbers we found: 6x² + 3x + 2x + 1.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
3x(2x + 1) + 1(2x + 1)
-
Factor out the common binomial: Notice that both terms now share the binomial (2x + 1). Factor it out:
(3x + 1)(2x + 1)
Therefore, the factored form of 6x² + 5x + 1 is (3x + 1)(2x + 1).
Method 2: Trial and Error
This method involves systematically trying different combinations of binomial factors until you find the correct one. While it may seem less structured than the AC method, it can be quicker once you develop a sense for it.
-
Consider the factors of the leading coefficient (a): The leading coefficient is 6. Its factors are (1, 6) and (2, 3).
-
Consider the factors of the constant term (c): The constant term is 1. Its only factors are (1, 1).
-
Test different combinations: We need to find a combination that, when multiplied using the FOIL method (First, Outer, Inner, Last), gives us the original expression. Let’s try some possibilities:
- (1x + 1)(6x + 1): This expands to 6x² + 7x + 1 (incorrect)
- (2x + 1)(3x + 1): This expands to 6x² + 5x + 1 (correct!)
Therefore, again, the factored form is (2x + 1)(3x + 1). Note that the order of the factors doesn't matter; (3x + 1)(2x + 1) is also correct.
Method 3: Using the Quadratic Formula (Indirect Factoring)
While not a direct factoring method, the quadratic formula can help find the roots of the quadratic equation 6x² + 5x + 1 = 0. These roots can then be used to determine the factors.
The quadratic formula is: x = [-b ± √(b² - 4ac)] / 2a
For our equation:
x = [-5 ± √(5² - 4 * 6 * 1)] / (2 * 6) x = [-5 ± √(25 - 24)] / 12 x = [-5 ± √1] / 12 x = (-5 ± 1) / 12
This gives us two solutions:
x₁ = (-5 + 1) / 12 = -4/12 = -1/3 x₂ = (-5 - 1) / 12 = -6/12 = -1/2
The factors are then found using the relationship between roots and factors: (x - x₁)(x - x₂). Substituting our roots:
(x + 1/3)(x + 1/2)
To get rid of the fractions, multiply each factor by the denominator of the fraction:
(3x + 1)(2x + 1)
Understanding the Underlying Mathematics
The success of these methods hinges on the distributive property (also known as the FOIL method) and the fundamental theorem of algebra, which states that a polynomial of degree n has exactly n roots (solutions) in the complex number system. In our case, the quadratic equation 6x² + 5x + 1 = 0 has two roots, which correspond to the factors we found. The AC method cleverly utilizes the distributive property in reverse to break down the trinomial into manageable parts.
Common Mistakes to Avoid
- Incorrect signs: Pay close attention to the signs of the terms when factoring. A misplaced negative sign can significantly alter the result.
- Missing factors: Ensure that you have considered all possible factor pairs of 'a' and 'c'.
- Incorrect application of the quadratic formula: Double-check your calculations when using the quadratic formula, paying attention to the order of operations and the signs.
- Forgetting to check your answer: Always expand your factored expression to verify it matches the original quadratic.
Frequently Asked Questions (FAQs)
- Q: Can all quadratic expressions be factored? A: Not all quadratic expressions can be factored using only integers. Some require the use of irrational numbers or complex numbers.
- Q: Is there only one correct way to factor a quadratic? A: While there might be different methods, the resulting factored form should be equivalent (ignoring the order of the factors).
- Q: What if the quadratic expression is difficult to factor? A: If you're struggling, use the quadratic formula to find the roots and then construct the factors from those roots. Practice will improve your ability to recognize factorable expressions more quickly.
- Q: How can I improve my factoring skills? A: Practice is key! Work through many different examples, using various methods, to build your confidence and speed.
Conclusion: Mastering Quadratic Factoring
Factoring quadratic expressions is a cornerstone of algebra. Understanding the different methods—the AC method, trial and error, and the indirect approach using the quadratic formula—provides a versatile toolkit for tackling these problems. By understanding the underlying mathematical principles and avoiding common errors, you'll not only improve your algebraic skills but also build a strong foundation for more advanced mathematical concepts. Remember, consistent practice is the key to mastering this essential skill. Through diligent effort, factoring quadratic expressions will become second nature, opening doors to a deeper understanding of the world of mathematics.
Latest Posts
Latest Posts
-
Gcf Of 35 And 50
Sep 13, 2025
-
What Is Factors Of 24
Sep 13, 2025
-
Meaning Of Snapped In Hindi
Sep 13, 2025
-
Helmholtz Coil Magnetic Field Formula
Sep 13, 2025
-
Whats 1 75 As A Fraction
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 6x 2 5x 1 Factor . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.