Whats 1.75 As A Fraction
thesills
Sep 13, 2025 · 5 min read
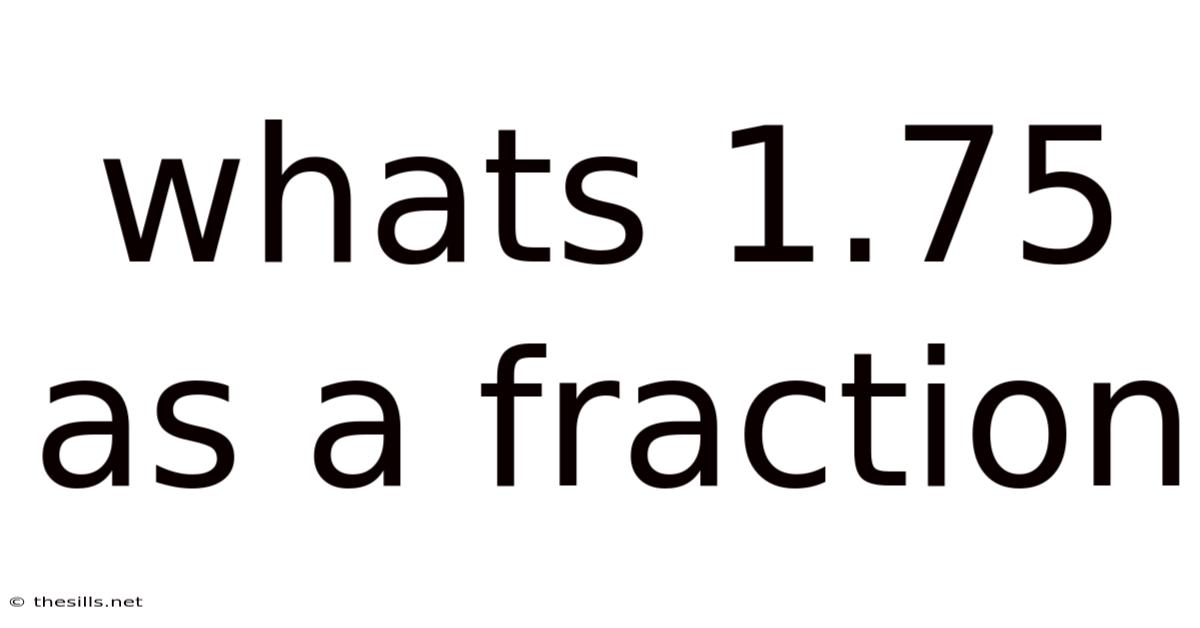
Table of Contents
What's 1.75 as a Fraction? A Comprehensive Guide
Understanding how to convert decimals to fractions is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the decimal 1.75 into its fractional equivalent, explaining the steps involved and providing additional context to solidify your understanding. We'll cover various methods, address common misconceptions, and delve into the underlying mathematical principles. This guide is designed for learners of all levels, from those just beginning to explore fractions to those looking to refresh their knowledge.
Understanding Decimals and Fractions
Before diving into the conversion, let's briefly review the concepts of decimals and fractions. A decimal is a way of representing a number using base-10, where the digits to the right of the decimal point represent fractions of powers of 10. For example, in 1.75, the '1' represents one whole unit, the '7' represents seven-tenths (7/10), and the '5' represents five-hundredths (5/100).
A fraction, on the other hand, represents a part of a whole, expressed as a ratio of two integers – the numerator (top number) and the denominator (bottom number). The denominator indicates the number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
Method 1: Using the Place Value System
The simplest way to convert 1.75 to a fraction is by understanding the place value of each digit.
-
Identify the whole number: The number to the left of the decimal point is the whole number part, which is 1 in this case.
-
Identify the decimal part: The digits to the right of the decimal point represent the fractional part. In 1.75, this is .75.
-
Express the decimal part as a fraction: The last digit (5) is in the hundredths place, meaning it represents 5/100. The digit before it (7) is in the tenths place, representing 7/10 or 70/100. Therefore, .75 can be written as 75/100.
-
Combine the whole number and the fraction: Since we have 1 whole unit and 75/100, we can write this as 1 + 75/100 = 1 75/100.
-
Simplify the fraction: To simplify the fraction, find the greatest common divisor (GCD) of the numerator (75) and the denominator (100). The GCD of 75 and 100 is 25. Divide both the numerator and denominator by 25: 75 ÷ 25 = 3 and 100 ÷ 25 = 4.
Therefore, 1 75/100 simplifies to 1 3/4.
Method 2: Using the Power of 10
This method is particularly useful when dealing with terminating decimals. A terminating decimal is a decimal that ends after a finite number of digits.
-
Write the decimal as a fraction with a power of 10 as the denominator: Since 1.75 has two digits after the decimal point, we write it as 175/100. This is because the decimal represents 175 hundredths.
-
Simplify the fraction: As shown in Method 1, we find the GCD of 175 and 100 (which is 25) and divide both the numerator and denominator by 25. This simplifies to 7/4.
-
Convert to a mixed number (if necessary): Since 7/4 is an improper fraction (numerator is greater than denominator), we convert it to a mixed number. Divide 7 by 4: 7 ÷ 4 = 1 with a remainder of 3. This means 7/4 is equal to 1 3/4.
Method 3: Understanding the Concept of Equivalence
The core concept behind decimal-to-fraction conversion is understanding equivalent fractions. Two fractions are equivalent if they represent the same value. For example, 1/2, 2/4, and 50/100 are all equivalent fractions.
To convert 1.75, we could think of it as 1 and 0.75. We know that 0.75 is 75 out of 100 parts, so we can represent it as 75/100. Then, we simplify this fraction by dividing both numerator and denominator by their GCD (25), yielding 3/4. Adding back the whole number 1, we get 1 3/4.
Addressing Common Misconceptions
-
Ignoring the whole number: A common mistake is to only consider the decimal part during conversion. Remember to include the whole number in your final answer.
-
Incorrect simplification: Always simplify your fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor. Failing to do so results in an inaccurate and less elegant representation.
-
Confusing numerator and denominator: Ensure you are placing the correct number in the numerator (the part of the whole) and the denominator (the total number of parts).
Further Exploration: Repeating Decimals
While 1.75 is a terminating decimal, it's crucial to understand how to handle repeating decimals, which have a digit or sequence of digits that repeat infinitely. Converting repeating decimals to fractions requires a different approach, usually involving algebraic manipulation.
Frequently Asked Questions (FAQ)
-
Q: Can I convert 1.75 to a percentage?
- A: Yes! 1.75 is equivalent to 175%. To convert a decimal to a percentage, simply multiply by 100.
-
Q: What other methods exist for converting decimals to fractions?
- A: While the methods described above are the most straightforward, more advanced techniques exist, particularly for repeating decimals. These involve using geometric series and algebraic manipulation.
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions presents the fraction in its most concise and efficient form. It makes calculations easier and allows for clearer comparisons between fractions.
-
Q: How do I convert a fraction back to a decimal?
- A: Simply divide the numerator by the denominator. For example, 3/4 = 3 ÷ 4 = 0.75.
Conclusion
Converting 1.75 to a fraction is a fundamental exercise in understanding the relationship between decimals and fractions. Through various methods—using place value, leveraging powers of 10, and recognizing equivalent fractions—we've shown that 1.75 is equivalent to 1 3/4 or 7/4. Mastering this conversion is key to advancing your mathematical skills and tackling more complex problems involving fractions and decimals. Remember to always simplify your fraction to its lowest terms and double-check your work to avoid common errors. By practicing these methods, you’ll build a strong foundation for future mathematical endeavors.
Latest Posts
Latest Posts
-
Is Methanol A Strong Base
Sep 13, 2025
-
Factor 4x 2 4x 3
Sep 13, 2025
-
Graphite Powder As A Lubricant
Sep 13, 2025
-
Bond Length And Bond Order
Sep 13, 2025
-
Three Features Of Cardiac Muscles
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Whats 1.75 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.