Factor 4x 2 4x 3
thesills
Sep 13, 2025 · 5 min read
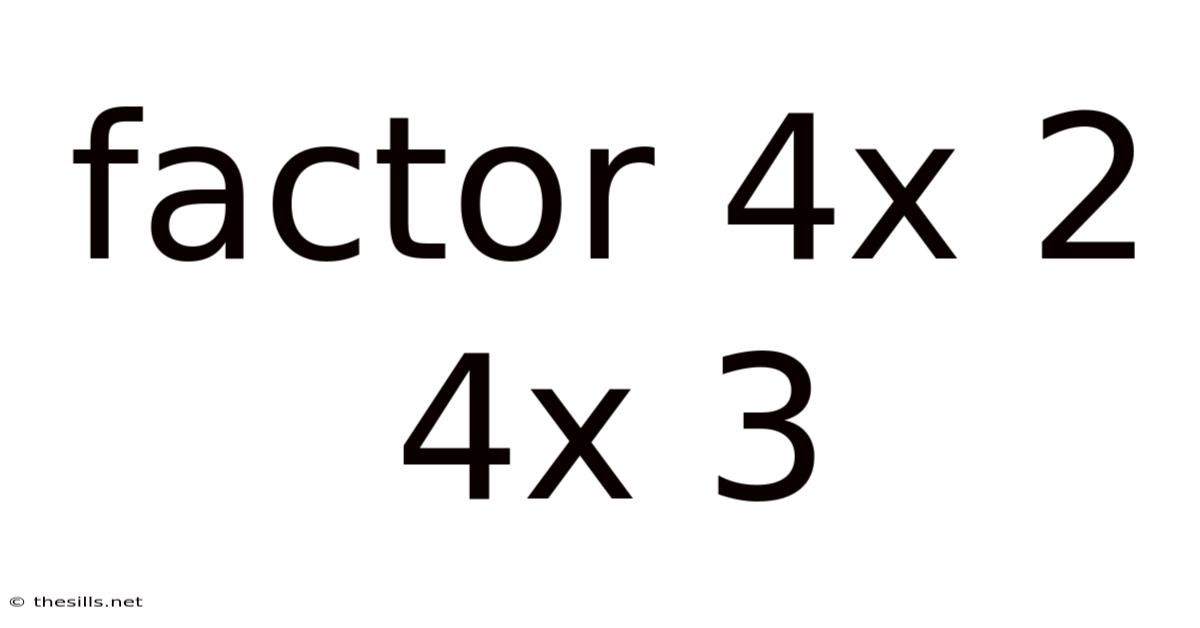
Table of Contents
Decomposing and Understanding 4x² + 4x + 3: A Comprehensive Guide
This article provides a detailed exploration of the expression 4x² + 4x + 3, covering its factorization, its graphical representation, and its applications in various mathematical contexts. Understanding this seemingly simple quadratic expression reveals fundamental concepts in algebra and prepares you for more complex mathematical challenges. We will delve into different methods of analyzing this expression, catering to various levels of mathematical understanding. This comprehensive guide will equip you with the tools to confidently tackle similar problems.
Introduction: What is a Quadratic Expression?
Before diving into the specifics of 4x² + 4x + 3, let's establish a foundational understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, 'x') is 2. The general form of a quadratic expression is ax² + bx + c, where 'a', 'b', and 'c' are constants (numbers), and 'a' is not equal to zero. Our expression, 4x² + 4x + 3, perfectly fits this general form, with a = 4, b = 4, and c = 3.
Attempting Factorization: The Challenges and Solutions
The most common approach to working with quadratic expressions is factorization. Factorization involves breaking down the expression into simpler expressions that, when multiplied together, give the original expression. However, factorizing 4x² + 4x + 3 presents a unique challenge. Unlike many quadratic expressions, this one doesn't readily factor using simple integer coefficients. Let's examine why:
-
Standard Factoring Methods: We typically look for two binomials (expressions with two terms) that multiply to give the quadratic. We might try different combinations of factors of 4 (the coefficient of x²) and 3 (the constant term), but no combination will yield the middle term of 4x.
-
The Discriminant: A powerful tool for understanding quadratic equations is the discriminant, denoted as Δ (Delta). The discriminant is calculated using the formula: Δ = b² - 4ac. In our case, Δ = (4)² - 4(4)(3) = 16 - 48 = -32. The significance of a negative discriminant is that the quadratic equation 4x² + 4x + 3 = 0 has no real roots. This implies that the quadratic expression cannot be factored into two linear expressions with real coefficients.
-
Complex Numbers: Since the discriminant is negative, the roots of the corresponding quadratic equation are complex numbers (involving the imaginary unit 'i', where i² = -1). This means that factorization is possible, but it will involve complex numbers.
Factorization Using the Quadratic Formula
To find the roots (and subsequently the factors) of the quadratic expression, we can use the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our expression:
x = [-4 ± √(-32)] / 8
Since √(-32) = √(16 * -2) = 4√(-2) = 4i√2 (where 'i' is the imaginary unit), we get:
x = [-4 ± 4i√2] / 8
Simplifying:
x = [-1 ± i√2] / 2
Therefore, the roots are:
x₁ = (-1 + i√2) / 2 x₂ = (-1 - i√2) / 2
These roots allow us to express the quadratic expression in factored form:
4x² + 4x + 3 = 4(x - x₁)(x - x₂) = 4(x - [(-1 + i√2) / 2])(x - [(-1 - i√2) / 2])
This is the complete factorization of the expression, although it involves complex numbers. This might seem less intuitive than factoring with real numbers, but it's a perfectly valid and important result.
Graphical Representation
The graph of the quadratic function y = 4x² + 4x + 3 is a parabola. Since the coefficient of x² (a = 4) is positive, the parabola opens upwards. The fact that the discriminant is negative means the parabola does not intersect the x-axis. In other words, the quadratic equation 4x² + 4x + 3 = 0 has no real solutions, which aligns with our previous findings. The vertex of the parabola (the lowest point) can be found using the formula x = -b/2a, which in this case is x = -4/(2*4) = -1/2. Substituting this value back into the equation gives the y-coordinate of the vertex.
Applications and Further Exploration
While the inability to factor this quadratic expression with real numbers might seem limiting, it highlights crucial concepts:
-
Complex Numbers in Algebra: This example demonstrates the significance of complex numbers in extending the solutions to algebraic equations beyond the real number system.
-
Quadratic Equations and Their Roots: Understanding the relationship between a quadratic expression, its roots, and its graphical representation is fundamental in algebra and calculus.
-
Completing the Square: Another technique to analyze quadratic expressions is "completing the square". While it won't lead to a factorization with real numbers in this case, it is a valuable tool for understanding the structure of the quadratic and finding its vertex.
-
Applications in Physics and Engineering: Quadratic equations frequently appear in physics and engineering problems, often modeling projectile motion, oscillations, and other phenomena. Even though the solutions might be complex, understanding how to work with these complex roots is often essential.
Frequently Asked Questions (FAQ)
Q1: Can 4x² + 4x + 3 be simplified further?
A1: No, the expression 4x² + 4x + 3 is already in its simplest form in terms of real numbers. The factorization involving complex numbers is the most complete factorization possible.
Q2: What does it mean if a quadratic expression cannot be factored using real numbers?
A2: It means that the corresponding quadratic equation has no real roots. Graphically, this translates to a parabola that does not intersect the x-axis. The roots are complex numbers.
Q3: Are there other methods to solve a quadratic equation besides the quadratic formula?
A3: Yes, other methods include factoring (when possible), completing the square, and graphical methods.
Q4: Why is the discriminant important?
A4: The discriminant helps determine the nature of the roots of a quadratic equation. A positive discriminant indicates two distinct real roots, a zero discriminant indicates one real root (a repeated root), and a negative discriminant indicates two complex roots.
Conclusion
The seemingly simple quadratic expression 4x² + 4x + 3 provides a rich learning opportunity. It underscores the importance of understanding the limitations of factoring with real numbers and introduces the concept of complex numbers as necessary extensions to the solution space of quadratic equations. Through the application of the quadratic formula and the interpretation of the discriminant, we can gain a deeper comprehension of quadratic expressions and their representation in both algebraic and graphical contexts. Mastering these concepts is crucial for further advancements in mathematics and its applications in various scientific and engineering disciplines. The exploration of this expression serves as a stepping stone to understanding more intricate mathematical concepts and problem-solving strategies.
Latest Posts
Latest Posts
-
Marginal And Total Utility Graph
Sep 14, 2025
-
C2h2 Sigma And Pi Bonds
Sep 14, 2025
-
No Bond Order In No3
Sep 14, 2025
-
D Dx X Log X
Sep 14, 2025
-
24 Percent As A Fraction
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Factor 4x 2 4x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.