D Dx X Log X
thesills
Sep 14, 2025 · 6 min read
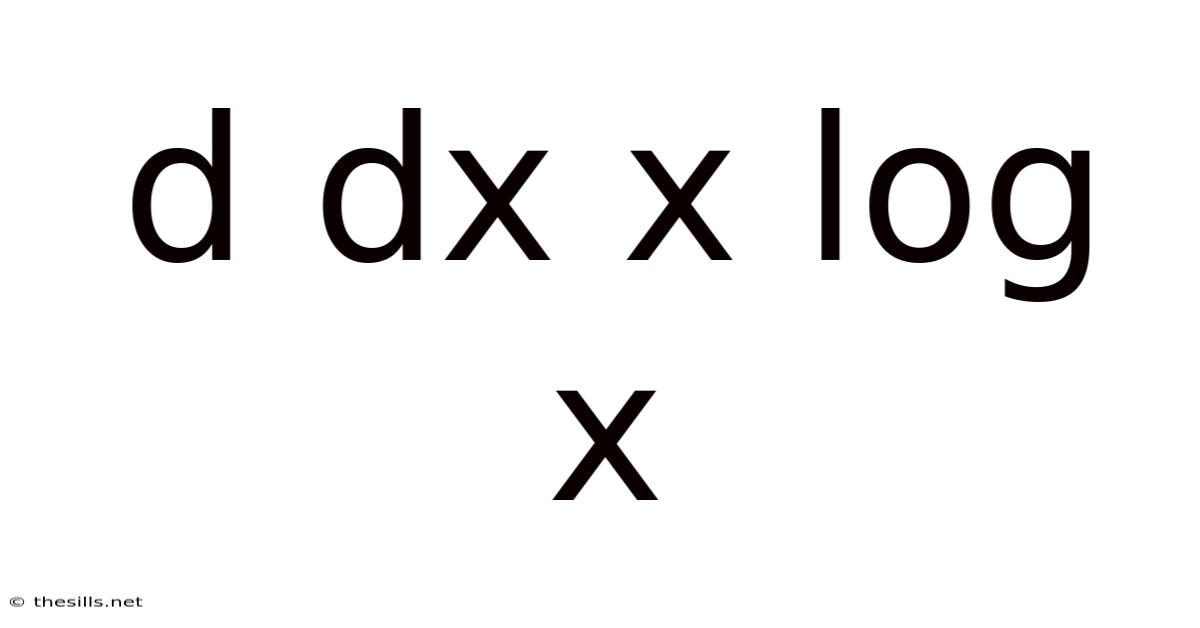
Table of Contents
Demystifying d/dx (x log x): A Comprehensive Guide
This article delves into the differentiation of the function x log x, a common problem encountered in calculus. We'll explore the process step-by-step, providing a detailed explanation suitable for both beginners and those seeking a deeper understanding. Understanding this derivative is crucial for various applications in mathematics, physics, and engineering, including optimization problems and solving differential equations. We'll cover the fundamental rules of differentiation, provide a clear and concise solution, and address frequently asked questions.
Introduction: Understanding Differentiation
Differentiation, a cornerstone of calculus, measures the instantaneous rate of change of a function. Geometrically, it represents the slope of the tangent line to the curve at a given point. The notation d/dx signifies differentiation with respect to the variable x. This means we're finding how the function changes as x changes infinitesimally.
Several rules govern differentiation, including the power rule, product rule, quotient rule, and chain rule. For the function x log x, we'll primarily utilize the product rule. The product rule states that the derivative of a product of two functions, u(x) and v(x), is given by:
d/dx [u(x)v(x)] = u'(x)v(x) + u(x)v'(x)
Where u'(x) and v'(x) represent the derivatives of u(x) and v(x) respectively.
Step-by-Step Differentiation of x log x
Let's apply the product rule to differentiate x log x. Here, we'll consider u(x) = x and v(x) = log x (assuming the natural logarithm, ln x, unless otherwise specified).
-
Identify u(x) and v(x):
- u(x) = x
- v(x) = log x
-
Find the derivatives u'(x) and v'(x):
- u'(x) = d/dx (x) = 1 (This is a simple application of the power rule)
- v'(x) = d/dx (log x) = 1/x (This is a fundamental derivative of the natural logarithm)
-
Apply the product rule:
d/dx (x log x) = u'(x)v(x) + u(x)v'(x) = (1)(log x) + (x)(1/x)
-
Simplify the expression:
d/dx (x log x) = log x + 1
Therefore, the derivative of x log x with respect to x is log x + 1.
A Deeper Dive: Understanding the Result
The result, log x + 1, reveals valuable insights into the behavior of the function x log x. The term 'log x' reflects the contribution of the logarithmic component to the rate of change. The constant term '+1' indicates that even when the logarithmic component's influence diminishes (as x approaches 0), there's still a constant positive rate of change.
This derivative can be used to find:
- Critical points: Setting the derivative equal to zero (log x + 1 = 0) allows us to find critical points where the function might have local maxima or minima. Solving this equation gives x = e<sup>-1</sup> = 1/e.
- Increasing/decreasing intervals: By analyzing the sign of the derivative, we can determine where the function is increasing (derivative > 0) or decreasing (derivative < 0). The function x log x is decreasing for 0 < x < 1/e and increasing for x > 1/e.
- Slope of the tangent line: At any given point x, the derivative log x + 1 represents the slope of the tangent line to the curve y = x log x.
Extending the Analysis: Different Logarithmic Bases
Our derivation used the natural logarithm (ln x). If the function is expressed using a different base, say base 10 (log₁₀ x), we need to adjust our approach using the change of base formula:
logₐ x = (logₓ x) / (logₓ a)
Where 'a' represents the base of the logarithm. For base 10, log₁₀ x = (ln x) / (ln 10).
Therefore, if we had the function x log₁₀ x, the differentiation process would be:
- Rewrite using natural logarithm: x log₁₀ x = x (ln x) / (ln 10)
- Apply the constant multiple rule: d/dx [x (ln x) / (ln 10)] = (1/ln 10) d/dx (x ln x)
- Apply the product rule (as before): (1/ln 10) (ln x + 1)
The derivative of x log₁₀ x is thus (ln x + 1) / ln 10.
Applications in Various Fields
The derivative of x log x finds applications in diverse fields:
- Information Theory: In information theory, the function x log x appears in the calculation of entropy, a measure of uncertainty or randomness in a system. The derivative helps analyze the rate of change of entropy with respect to the probability distribution.
- Physics: The function and its derivative can model various physical phenomena where logarithmic and linear relationships are intertwined. For instance, in certain thermodynamic processes or diffusion models.
- Computer Science: Algorithms and data structures frequently involve logarithmic complexities. The derivative helps in analyzing the performance and scalability of these algorithms.
- Economics: In economics, logarithmic functions often represent utility or production functions. The derivative provides insights into marginal utility or marginal productivity.
Frequently Asked Questions (FAQ)
Q1: What if the function is x log(x²) instead of x log x?
A1: Use the properties of logarithms to simplify the function first: x log(x²) = 2x log x. Then apply the product rule as shown above, resulting in a derivative of 2(log x + 1) = 2 log x + 2.
Q2: Can we use the chain rule here?
A2: While the chain rule isn't directly applicable in its most basic form, the product rule, in essence, incorporates the principles of the chain rule when dealing with composite functions. The product rule is a more efficient approach in this case.
Q3: What about the derivative of x log|x|?
A3: The absolute value introduces a piecewise function. The derivative would be log|x| + 1 for x ≠ 0. The point x=0 is a point of non-differentiability due to the discontinuity of the function.
Q4: What happens when x approaches 0?
A4: The function x log x approaches 0 as x approaches 0. However, the derivative log x + 1 approaches negative infinity as x approaches 0 from the positive side.
Q5: How can I visualize this derivative graphically?
A5: Graphing both the original function y = x log x and its derivative y = log x + 1 on the same axes will provide a visual representation of the relationship between the function and its rate of change. The derivative's value at any given point corresponds to the slope of the tangent to the original function at that point.
Conclusion: Mastering the Derivative of x log x
The derivative of x log x, which is log x + 1 (for the natural logarithm), is a fundamental result with widespread applications. By understanding the step-by-step process of differentiation using the product rule, and by grasping the implications of the resulting derivative, one gains a powerful tool for analyzing the behavior of this important function. Remember to adapt the approach based on the specific logarithmic base used and to consider potential discontinuities or special cases like x approaching 0. With practice and a solid understanding of the underlying principles, you'll confidently tackle more complex differentiation problems.
Latest Posts
Latest Posts
-
According To Law Of Demand
Sep 14, 2025
-
Ozymandias Percy Bysshe Shelley Analysis
Sep 14, 2025
-
Lewis Dot Structure For Mgo
Sep 14, 2025
-
Nonaqueous Solutions Do Not Have
Sep 14, 2025
-
Rod Mass Moment Of Inertia
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about D Dx X Log X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.