X 2 3x 24 0
thesills
Sep 13, 2025 · 4 min read
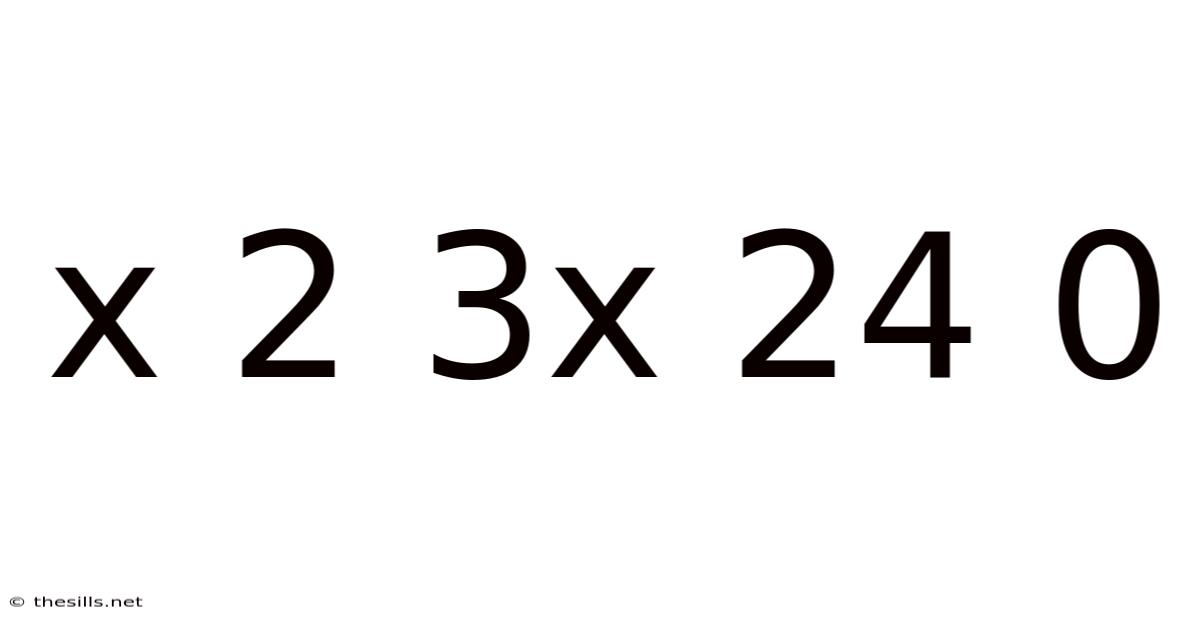
Table of Contents
Decoding the Mathematical Puzzle: x² + 3x² = 240
This article delves into the solution of the mathematical equation x² + 3x² = 240, exploring various approaches to solving quadratic equations and providing a detailed explanation suitable for students and enthusiasts alike. We'll cover the fundamental concepts, step-by-step solutions, and even touch upon the broader context of quadratic equations in mathematics. This comprehensive guide aims to not just provide the answer but also enhance your understanding of the underlying principles.
Introduction: Understanding Quadratic Equations
Before diving into the solution of x² + 3x² = 240, let's establish a foundational understanding of quadratic equations. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually 'x') is 2. The general form of a quadratic equation is ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our given equation, while seemingly simpler, falls under the umbrella of quadratic equations because it can be simplified into the standard form.
Step-by-Step Solution: Solving x² + 3x² = 240
The beauty of this equation lies in its simplicity. Notice that both terms on the left-hand side contain x². This allows us to combine like terms immediately:
- Combine Like Terms: x² + 3x² = 4x²
This simplifies our equation to:
4x² = 240
- Isolate x²: To isolate x², we need to divide both sides of the equation by 4:
4x²/4 = 240/4
This simplifies to:
x² = 60
- Solve for x: To find the value of x, we need to take the square root of both sides of the equation. Remember that when taking the square root, we consider both positive and negative solutions:
√x² = ±√60
This gives us:
x = ±√60
- Simplify the Radical: The number 60 can be simplified by factoring out perfect squares. 60 can be factored as 2² * 3 * 5. Therefore:
x = ±√(2² * 3 * 5) = ±2√15
Therefore, the solutions to the equation x² + 3x² = 240 are x = 2√15 and x = -2√15.
Understanding the Solutions: Positive and Negative Roots
The presence of both a positive and a negative solution (+2√15 and -2√15) is a characteristic feature of many quadratic equations. This is because squaring a positive or a negative number results in a positive number. In our case, both (2√15)² and (-2√15)² will equal 60, satisfying the equation.
Graphical Representation: Visualizing the Solution
While not strictly necessary to solve this particular equation, visualizing it graphically can enhance understanding. The equation 4x² = 240 represents a parabola. The solutions (2√15 and -2√15) represent the x-intercepts – the points where the parabola intersects the x-axis.
Expanding the Understanding: Other Methods for Solving Quadratic Equations
While the direct approach used above was efficient for this specific equation, let's explore other methods applicable to more complex quadratic equations:
-
Factoring: This method involves expressing the quadratic equation as a product of two linear factors. It's particularly useful when the equation can be easily factored.
-
Quadratic Formula: The quadratic formula is a general formula that provides the solutions for any quadratic equation of the form ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / 2a
This formula is invaluable when factoring isn't readily apparent.
- Completing the Square: This method involves manipulating the equation to create a perfect square trinomial, making it easier to solve.
Frequently Asked Questions (FAQ)
- Q: Can this equation be solved without simplifying first?
A: Yes, although less efficiently. You could substitute the values directly into the equation and then solve, but combining like terms first streamlines the process.
- Q: What if the equation was x² + 3x² = -240?
A: In this case, after combining like terms, you would get 4x² = -240. Dividing by 4 gives x² = -60. Since the square of a real number cannot be negative, there would be no real solutions. The solutions would be complex numbers involving the imaginary unit 'i' (where i² = -1).
- Q: What is the significance of the ± symbol?
A: The ± (plus-minus) symbol indicates that there are two possible solutions – one positive and one negative. This is inherent to the nature of square roots.
- Q: How can I check if my solutions are correct?
A: Substitute the solutions back into the original equation (x² + 3x² = 240). If both sides of the equation are equal, your solutions are correct. Let's check for x = 2√15:
(2√15)² + 3(2√15)² = 60 + 3(60) = 60 + 180 = 240
The equation holds true. The same applies to x = -2√15.
Conclusion: Mastering Quadratic Equations
Solving x² + 3x² = 240 showcases the fundamental principles of solving quadratic equations. Understanding the different methods, including combining like terms, simplifying radicals, and interpreting both positive and negative solutions, is crucial for tackling more complex problems. This equation, while seemingly simple, serves as a stepping stone to a deeper comprehension of quadratic equations and their applications in various fields of mathematics and beyond. Remember to always practice and explore different approaches to solidify your understanding. The key to mastering any mathematical concept is consistent practice and a curious mindset. Keep exploring, keep questioning, and keep learning!
Latest Posts
Latest Posts
-
How To Calculate Q Value
Sep 13, 2025
-
Factor 6x 2 5x 6
Sep 13, 2025
-
Roots Of A Complex Number
Sep 13, 2025
-
But 1 En 3 Yne
Sep 13, 2025
-
Chemical Equation For Distilled Water
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about X 2 3x 24 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.