X 2 3x 2 Simplify
thesills
Sep 18, 2025 · 6 min read
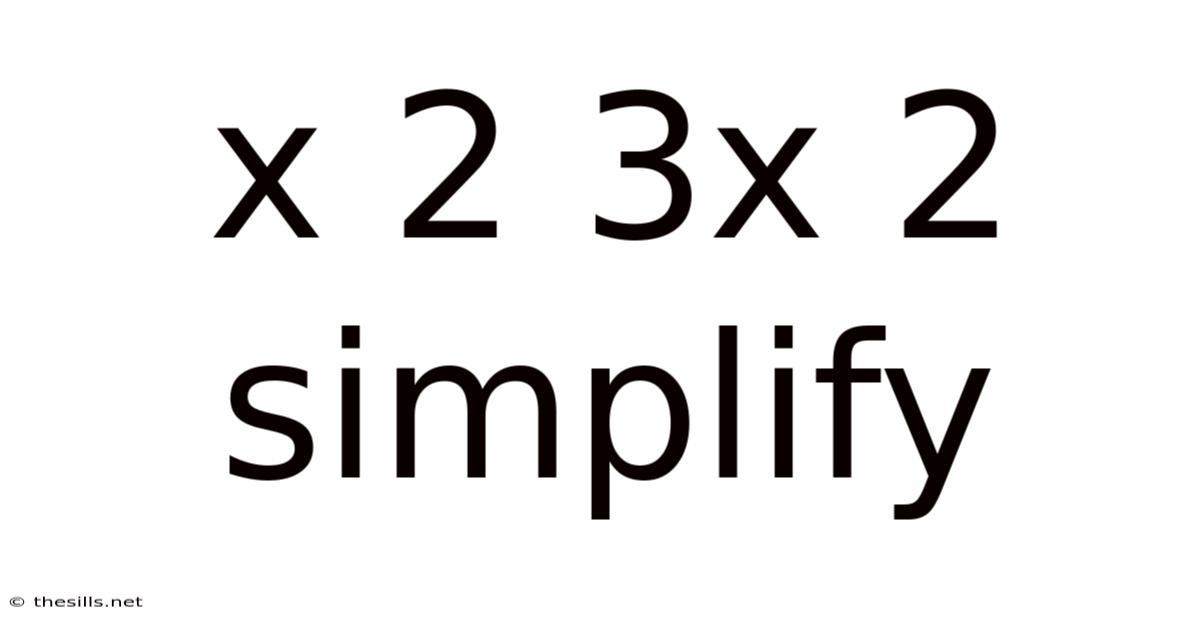
Table of Contents
Simplifying Algebraic Expressions: A Deep Dive into x² + 3x²
This article provides a comprehensive guide to simplifying the algebraic expression x² + 3x². We'll explore the fundamental principles of combining like terms, delve into the reasons behind the simplification process, and address common misconceptions. Understanding this seemingly simple expression lays the groundwork for mastering more complex algebraic manipulations crucial in various fields, from physics and engineering to finance and computer science. This detailed explanation will equip you with the knowledge and confidence to tackle similar problems.
Understanding the Basics: What are Like Terms?
Before we simplify x² + 3x², let's establish a fundamental concept in algebra: like terms. Like terms are terms that have the same variables raised to the same powers. For instance:
- 3x and 5x are like terms because they both have the variable 'x' raised to the power of 1.
- 2x² and -7x² are like terms because they both have the variable 'x' raised to the power of 2.
- 4xy and -2xy are like terms because they both have the variables 'x' and 'y', each raised to the power of 1.
Conversely, these are not like terms:
- 2x and 2x²: The powers of 'x' are different (1 and 2).
- 3x and 3y: The variables are different.
- 4x²y and 4xy²: The powers of the variables are different.
Identifying like terms is crucial for simplification. Only like terms can be combined.
Simplifying x² + 3x²: A Step-by-Step Approach
Now, let's tackle the expression x² + 3x². Notice that both terms, x² and 3x², are like terms because they both contain the variable 'x' raised to the power of 2. To simplify, we combine the coefficients (the numbers multiplying the variables).
Step 1: Identify the like terms. In this case, both terms are like terms: x² and 3x².
Step 2: Add the coefficients. The coefficient of the first term, x², is 1 (although it's not explicitly written, it's understood to be there). The coefficient of the second term, 3x², is 3. Adding these coefficients gives us 1 + 3 = 4.
Step 3: Write the simplified expression. The simplified expression is 4x².
Therefore, x² + 3x² = 4x².
The Distributive Property and its Relevance
The simplification process we just followed is directly related to the distributive property of algebra. The distributive property states that for any numbers a, b, and c:
a(b + c) = ab + ac
While it may not seem immediately apparent, the distributive property underpins our simplification. We can rewrite x² + 3x² as:
1x² + 3x²
Now, we can factor out the common term x²:
x²(1 + 3)
Using the distributive property in reverse, we get:
x²(4) = 4x²
This demonstrates that simplifying like terms is essentially an application of the distributive property, allowing us to efficiently combine similar expressions.
Beyond the Basics: Exploring More Complex Scenarios
The principle of combining like terms extends to more complex algebraic expressions involving multiple variables and higher powers. Consider the following examples:
-
2x²y + 5x²y - x²y: Here, all three terms are like terms. Combining their coefficients (2 + 5 - 1 = 6) results in the simplified expression 6x²y.
-
3x³ + 2x² + 5x³ - x²: This expression has two sets of like terms: the x³ terms and the x² terms. Simplifying separately, we get: (3x³ + 5x³) + (2x² - x²) = 8x³ + x².
-
4xy² + 2x²y - xy² + 3x²y: This expression has two sets of like terms: the xy² terms and the x²y terms. Simplifying separately we get: (4xy² - xy²) + (2x²y + 3x²y) = 3xy² + 5x²y. Note that these simplified terms cannot be further combined as they are not like terms.
Common Mistakes to Avoid
Several common mistakes can hinder the accurate simplification of algebraic expressions. Understanding these pitfalls will enhance your accuracy:
-
Incorrectly combining unlike terms: Remember, only like terms can be combined. Avoid adding or subtracting terms with different variables or different powers of the same variable.
-
Errors in arithmetic: Double-check your addition and subtraction. Simple arithmetic errors can lead to incorrect results.
-
Forgetting the coefficient of 1: When a term has no visible coefficient, it’s implicitly 1. Don’t forget to include it when combining like terms.
Visualizing the Simplification: A Geometric Approach
We can visualize the simplification of x² + 3x² using geometric shapes. If we represent x² as a square with sides of length x, then x² represents the area of that square. Similarly, 3x² can be represented as three such squares. Combining them visually shows that the total area is equivalent to four squares with sides of length x, or 4x². This geometric interpretation provides an intuitive understanding of the algebraic simplification.
The Significance of Simplification in Mathematics and Beyond
Simplifying algebraic expressions is a fundamental skill in mathematics, crucial for solving equations, manipulating formulas, and understanding relationships between variables. This skill is not confined to the realm of pure mathematics; it has far-reaching applications in other fields:
-
Physics and Engineering: Simplifying equations is essential for solving problems in mechanics, electricity, and many other branches of physics and engineering.
-
Computer Science: Simplifying algorithms and code improves efficiency and readability.
-
Finance: Simplifying financial models helps in making informed decisions about investments and risk management.
-
Data Analysis: Simplifying complex datasets makes them easier to understand and interpret.
Frequently Asked Questions (FAQ)
Q1: What if I have an expression like x² + 2x + 3x²?
A1: This expression contains two sets of like terms: x² and 3x², and the term 2x which is unlike the others. First, combine the like terms: x² + 3x² = 4x². Then, you'll have 4x² + 2x. These cannot be further combined because they are unlike terms.
Q2: Can I simplify x² + y²?
A2: No. x² and y² are unlike terms because they involve different variables. They cannot be simplified further.
Q3: What if the coefficients are fractions or decimals?
A3: The process remains the same. You add or subtract the coefficients as usual. For example: 0.5x² + 1.5x² = 2x². Or (1/2)x² + (3/2)x² = 2x².
Q4: What about negative coefficients?
A4: Treat negative coefficients like negative numbers in regular addition and subtraction. For example: 5x² - 2x² = 3x².
Q5: How does this relate to factoring?
A5: Factoring is the reverse of expanding. While simplifying combines like terms, factoring pulls out common factors. For example, 4x² + 2x can be factored as 2x(2x + 1). Factoring and simplifying are both essential algebraic techniques often used in conjunction.
Conclusion: Mastering the Fundamentals
Simplifying algebraic expressions like x² + 3x² is a foundational skill in mathematics. By understanding the concept of like terms and applying the principles of combining coefficients, you can efficiently simplify complex expressions. This skill, grounded in the distributive property, is crucial not only for academic success but also for applications in various fields. Mastering this fundamental concept will pave the way for tackling more advanced algebraic concepts and problems with confidence. Remember the key steps: identify like terms, add or subtract their coefficients, and write the simplified expression. Practice regularly, and you'll quickly develop proficiency in this essential algebraic skill.
Latest Posts
Latest Posts
-
20 35 In Lowest Terms
Sep 18, 2025
-
2 Methyl 1 3 Butadiene
Sep 18, 2025
-
What Is Malleability And Ductility
Sep 18, 2025
-
Fermentation Of Milk To Yogurt
Sep 18, 2025
-
Integration Of Sin Inverse X
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about X 2 3x 2 Simplify . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.