X 2 2x 9 0
thesills
Sep 12, 2025 · 5 min read
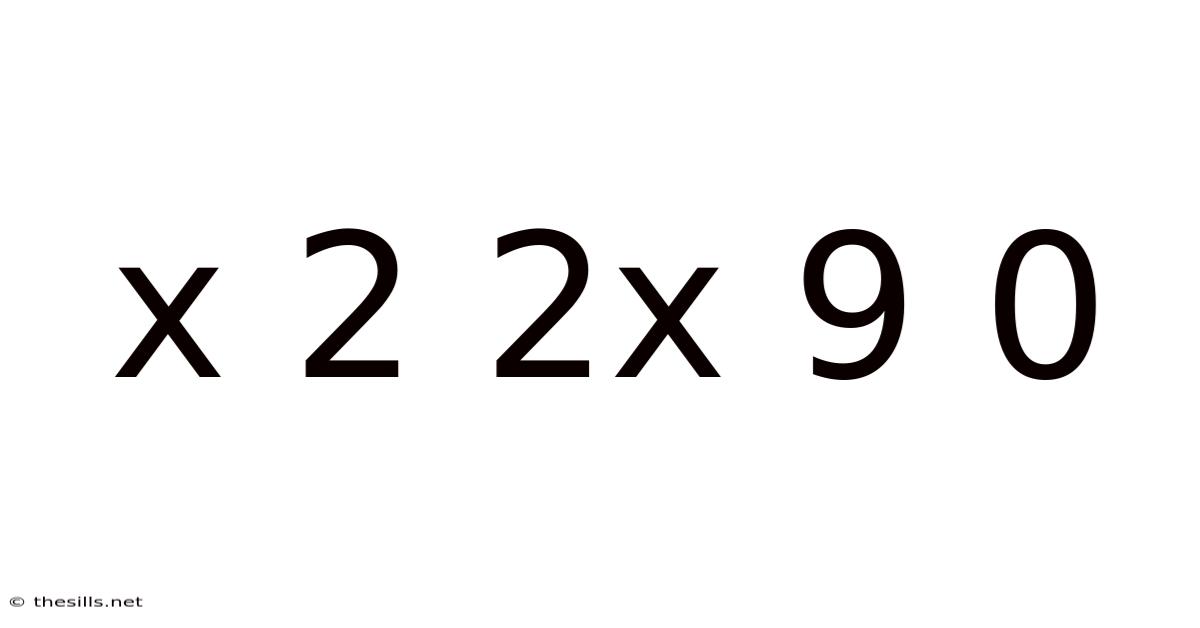
Table of Contents
Decoding the Mystery: Exploring the Mathematical Sequence "x 2 2x 9 0"
This article delves into the intriguing mathematical sequence "x 2 2x 9 0," exploring its potential interpretations, underlying principles, and possible solutions. We will move beyond simply finding a numerical answer and unpack the various mathematical concepts it can represent, making it accessible to a wide range of readers, from high school students to those with a more advanced mathematical background. This exploration will demonstrate how seemingly simple sequences can lead to a richer understanding of algebra and problem-solving.
Understanding the Problem: Different Interpretations
At first glance, "x 2 2x 9 0" appears ambiguous. The lack of explicit operators between the elements leaves room for multiple interpretations. This ambiguity is a crucial aspect of the problem, highlighting the importance of precise mathematical notation. Let's explore some plausible interpretations:
-
Interpretation 1: A Quadratic Equation: The most likely interpretation is that this represents a quadratic equation. Assuming the spaces represent addition and equality, we can rewrite it as:
x + 2 + 2x + 9 = 0. This is a standard form of a quadratic equation that we can solve using various methods. -
Interpretation 2: A Sequence with Missing Operators: We could consider it a sequence where some operators are missing. For example, it might represent a sequence where multiplication, division, or other operations are implied between the elements. This interpretation requires making assumptions and testing different combinations of operations.
-
Interpretation 3: A Symbolic Representation: It's possible that the sequence represents a more abstract concept within a broader mathematical context. Without additional information, this interpretation is highly speculative but worth considering when dealing with complex mathematical notations.
Solving as a Quadratic Equation: A Step-by-Step Approach
Let's focus on the most probable interpretation: solving it as a quadratic equation. We'll use the equation derived from Interpretation 1: x + 2 + 2x + 9 = 0.
Step 1: Simplify the Equation: Combine like terms:
3x + 11 = 0
Step 2: Isolate the Variable: Subtract 11 from both sides:
3x = -11
Step 3: Solve for x: Divide both sides by 3:
x = -11/3 or approximately x ≈ -3.67
Therefore, if the sequence represents a quadratic equation, the solution for x is -11/3.
Exploring Other Potential Interpretations: The Power of Assumption and Testing
Now let's briefly investigate the possibility of missing operators. Since there's no clear indication of what those operators might be, we'll need to engage in a systematic trial-and-error approach. Let's test a few possibilities:
-
Scenario 1: Multiplication and Addition: Let's assume multiplication between 'x' and '2', and addition between the other elements. The equation could become:
x * 2 + 2x + 9 = 0. This simplifies to4x + 9 = 0, which leads tox = -9/4orx ≈ -2.25. -
Scenario 2: All Addition: This interpretation would require adding all numbers, including the 'x' terms, which leads back to the quadratic equation discussed above.
-
Scenario 3: A Combination of Operations: The possibilities here are numerous and would require more context or information to guide our assumptions. We might experiment with different combinations of multiplication, division, addition, and subtraction, but without additional constraints, this is likely to lead to a vast number of possible solutions, without a definitive answer.
The Importance of Context and Precise Notation in Mathematics
The ambiguity of the sequence "x 2 2x 9 0" underscores the critical importance of precise mathematical notation. The lack of clear operators significantly impacts the interpretation and solution. In real-world applications, especially in fields like programming, engineering, and scientific research, clear and unambiguous notation is essential to avoid errors and ensure accurate results.
Expanding the Understanding: Beyond Simple Equations
The initial problem, even in its most straightforward interpretation as a quadratic equation, can serve as a springboard to explore more advanced mathematical concepts.
-
Quadratic Formula: The quadratic formula provides a general solution for any quadratic equation in the form
ax² + bx + c = 0. While our simplified equation didn't require the quadratic formula, it's a powerful tool to understand the underlying structure of quadratic equations and their solutions. -
Graphing Quadratic Equations: Visualizing the quadratic equation
3x + 11 = 0as a graph helps understand the relationship between the equation, its solution (the x-intercept), and the overall behavior of the function. -
Complex Numbers: Although this specific example yields a real number solution, quadratic equations can have complex number solutions (involving the imaginary unit i). Exploring complex numbers can broaden your mathematical horizons.
Frequently Asked Questions (FAQ)
-
Q: What if there were more numbers in the sequence?
A: With more numbers, the complexity would increase. It might still represent a polynomial equation of a higher degree, a more complex sequence, or require further clarification about the operations involved.
-
Q: How can I improve my ability to solve these types of problems?
A: Practice solving various types of equations, starting with simpler ones and gradually increasing the complexity. Understanding fundamental algebraic concepts is key. Look for patterns and practice translating word problems into mathematical equations.
-
Q: Are there other mathematical contexts where this sequence might appear?
A: While this specific sequence isn't widely known within a specific named mathematical context, similar sequences can appear in various areas, including:
- Difference equations: These equations relate the values of a sequence to previous values.
- Linear algebra: Systems of linear equations can involve similar patterns of numbers and variables.
- Coding and algorithms: Sequences are fundamental elements in many computational processes.
Conclusion: Unveiling the Power of Mathematical Reasoning
The seemingly simple sequence "x 2 2x 9 0" has led us on a journey exploring different mathematical interpretations, solving techniques, and underlying principles. This exploration highlights the critical role of clear notation and the importance of systematic problem-solving techniques. While the most likely solution is found by treating it as a simple quadratic equation, the exercise serves as a reminder that exploring alternative possibilities is essential in mathematical problem-solving. By embracing ambiguity and employing a structured approach, we can unlock a deeper understanding of the elegance and power of mathematics. The journey of mathematical exploration is not about finding a single correct answer but about developing the skills to approach problems critically, creatively, and systematically. This problem, despite its simplicity, effectively showcases the beauty and complexity of mathematical reasoning.
Latest Posts
Latest Posts
-
Lowest Term Of 8 12
Sep 12, 2025
-
X 2 X 2 1
Sep 12, 2025
-
Sum From 1 To 30
Sep 12, 2025
-
Angular Speed Of Minute Hand
Sep 12, 2025
-
24 24 24 24 24
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x 9 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.