X 2 2x 1 0
thesills
Sep 13, 2025 · 6 min read
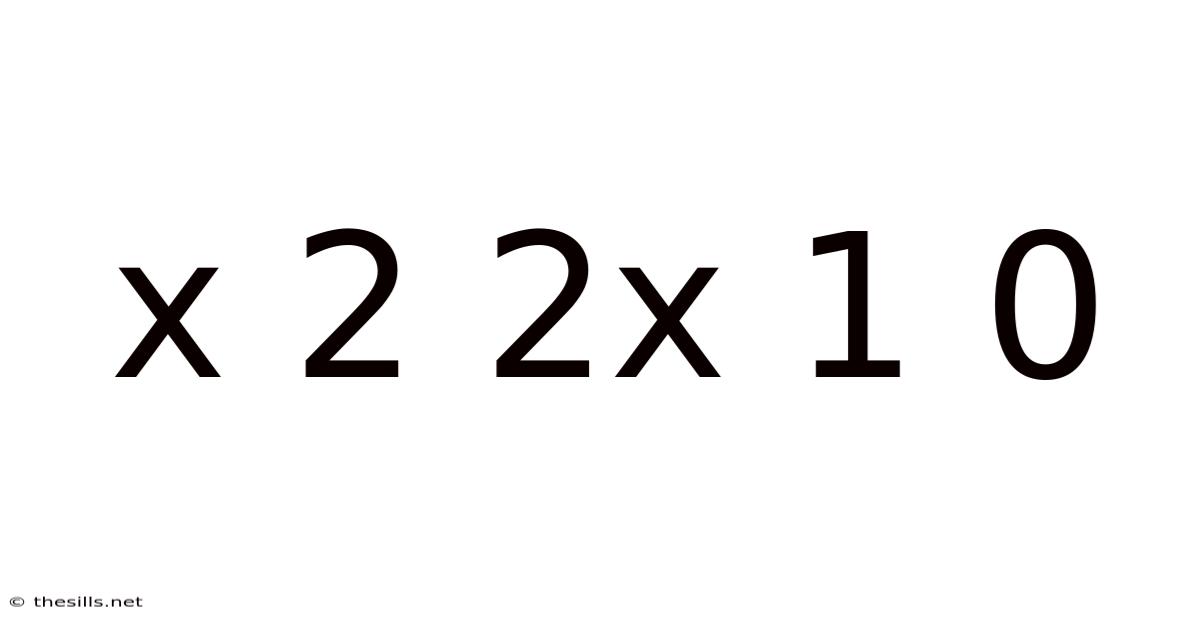
Table of Contents
Decoding the Enigma: A Deep Dive into x² + 2x + 1 = 0
The seemingly simple quadratic equation, x² + 2x + 1 = 0, serves as a gateway to understanding fundamental concepts in algebra. This equation, while straightforward in appearance, unlocks a wealth of knowledge regarding factoring, the quadratic formula, and the nature of roots. This article will dissect this equation, exploring its solutions, the underlying mathematical principles, and its broader implications in mathematics and beyond. We'll move beyond simply finding the answer to truly grasp the "why" behind the solution.
Introduction: Understanding Quadratic Equations
Before diving into the specifics of x² + 2x + 1 = 0, let's establish a basic understanding of quadratic equations. A quadratic equation is any equation that can be written in the standard form: ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. The highest power of the variable 'x' is 2, hence the term "quadratic." These equations often represent parabolic curves when graphed, and finding their solutions (also called roots or zeros) means identifying the x-values where the parabola intersects the x-axis.
Method 1: Factoring the Quadratic Expression
The most elegant and often the quickest way to solve x² + 2x + 1 = 0 is through factoring. Factoring involves expressing the quadratic expression as a product of simpler expressions. Notice that x² + 2x + 1 is a perfect square trinomial. This means it can be factored into the square of a binomial.
Observe the pattern: (x + y)² = x² + 2xy + y². In our equation, we have x² + 2x + 1. If we compare this to the perfect square trinomial pattern, we see that:
- x² corresponds to x²
- 2x corresponds to 2xy, implying y = 1
- 1 corresponds to y² (since 1² = 1)
Therefore, x² + 2x + 1 can be factored as (x + 1)(x + 1) or (x + 1)².
Now, we set the factored expression equal to zero:
(x + 1)² = 0
Taking the square root of both sides, we get:
x + 1 = 0
Solving for x, we find:
x = -1
This means the equation x² + 2x + 1 = 0 has only one solution, or one real root, which is x = -1. This is a case of a repeated root, meaning the parabola touches the x-axis at only one point.
Method 2: Utilizing the Quadratic Formula
The quadratic formula is a powerful tool that can solve any quadratic equation, regardless of whether it factors easily. The formula is derived from completing the square and is given by:
x = [-b ± √(b² - 4ac)] / 2a
For our equation, x² + 2x + 1 = 0, we have a = 1, b = 2, and c = 1. Substituting these values into the quadratic formula:
x = [-2 ± √(2² - 4 * 1 * 1)] / (2 * 1)
x = [-2 ± √(4 - 4)] / 2
x = [-2 ± √0] / 2
x = -2 / 2
x = -1
Again, we arrive at the solution x = -1. The quadratic formula confirms our result obtained through factoring. The fact that the discriminant (b² - 4ac) equals zero indicates that there is only one real root.
Method 3: Completing the Square
Completing the square is another algebraic technique for solving quadratic equations. It involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
Starting with x² + 2x + 1 = 0:
-
Move the constant term to the right side of the equation: x² + 2x = -1
-
Take half of the coefficient of the x term (which is 2), square it (1² = 1), and add it to both sides of the equation: x² + 2x + 1 = -1 + 1
-
The left side is now a perfect square trinomial: (x + 1)² = 0
-
Solve for x as before: x = -1
Completing the square provides a systematic approach to solving quadratic equations, especially useful when factoring isn't immediately apparent.
Graphical Representation and Interpretation
Graphing the quadratic equation y = x² + 2x + 1 provides a visual representation of its solution. The graph is a parabola that opens upwards. The vertex of this parabola is at the point (-1, 0). The x-intercept, where the parabola intersects the x-axis, represents the solution(s) to the equation x² + 2x + 1 = 0. In this case, the parabola only touches the x-axis at x = -1, confirming our earlier findings that there's only one real root.
The Significance of the Discriminant (b² - 4ac)
The expression b² - 4ac within the quadratic formula is called the discriminant. It provides crucial information about the nature of the roots of a quadratic equation:
- b² - 4ac > 0: The equation has two distinct real roots. The parabola intersects the x-axis at two different points.
- b² - 4ac = 0: The equation has one real root (a repeated root). The parabola touches the x-axis at only one point.
- b² - 4ac < 0: The equation has no real roots. The parabola does not intersect the x-axis; its roots are complex numbers (involving the imaginary unit 'i').
In our equation x² + 2x + 1 = 0, the discriminant is 0, indicating the presence of only one real root, which is x = -1.
Applications in Real-World Scenarios
While seemingly abstract, quadratic equations have numerous real-world applications. They are used in:
- Physics: Calculating projectile motion, determining the trajectory of objects under gravity.
- Engineering: Designing bridges, buildings, and other structures.
- Economics: Modeling supply and demand curves, analyzing market trends.
- Computer Graphics: Creating curves and shapes in computer-generated images.
Understanding quadratic equations and their solutions is essential for solving problems in these and other fields.
Frequently Asked Questions (FAQ)
-
Q: What does it mean when a quadratic equation has only one solution?
- A: It means the parabola representing the equation touches the x-axis at only one point. This point represents the single real solution to the equation. The solution is also referred to as a repeated root.
-
Q: Can a quadratic equation have no solutions?
- A: Yes, if the discriminant (b² - 4ac) is negative, the equation has no real solutions. The solutions are then complex numbers involving the imaginary unit 'i'.
-
Q: Why is factoring a preferred method when possible?
- A: Factoring is often faster and simpler than using the quadratic formula, especially for equations with easily recognizable patterns like perfect square trinomials.
-
Q: What if 'a' in the quadratic equation ax² + bx + c = 0 is equal to zero?
- A: If 'a' is zero, the equation is no longer quadratic; it becomes a linear equation of the form bx + c = 0, which is much easier to solve.
Conclusion: Beyond the Equation
The equation x² + 2x + 1 = 0, while seemingly simple, provides a robust platform to understand core concepts in algebra. By exploring its solution using factoring, the quadratic formula, and completing the square, we gain a deeper appreciation for the interconnectedness of these algebraic techniques. Understanding the discriminant allows us to predict the nature of solutions without actually solving the equation. Furthermore, the broad applications of quadratic equations highlight their importance in various fields, emphasizing the relevance of mathematical principles to real-world problems. The journey of solving this simple equation serves as a stepping stone to mastering more complex mathematical concepts and problem-solving skills. Remember, the beauty of mathematics lies not just in finding the answer, but in understanding the underlying principles and their profound implications.
Latest Posts
Latest Posts
-
Is Gasoline A Pure Substance
Sep 13, 2025
-
Pressure Of Column Of Water
Sep 13, 2025
-
2x X 2x X 2x
Sep 13, 2025
-
Liters To Kilograms Of Water
Sep 13, 2025
-
What Is 12 Of 75000
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x 1 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.