2x X 2x X 2x
thesills
Sep 13, 2025 · 6 min read
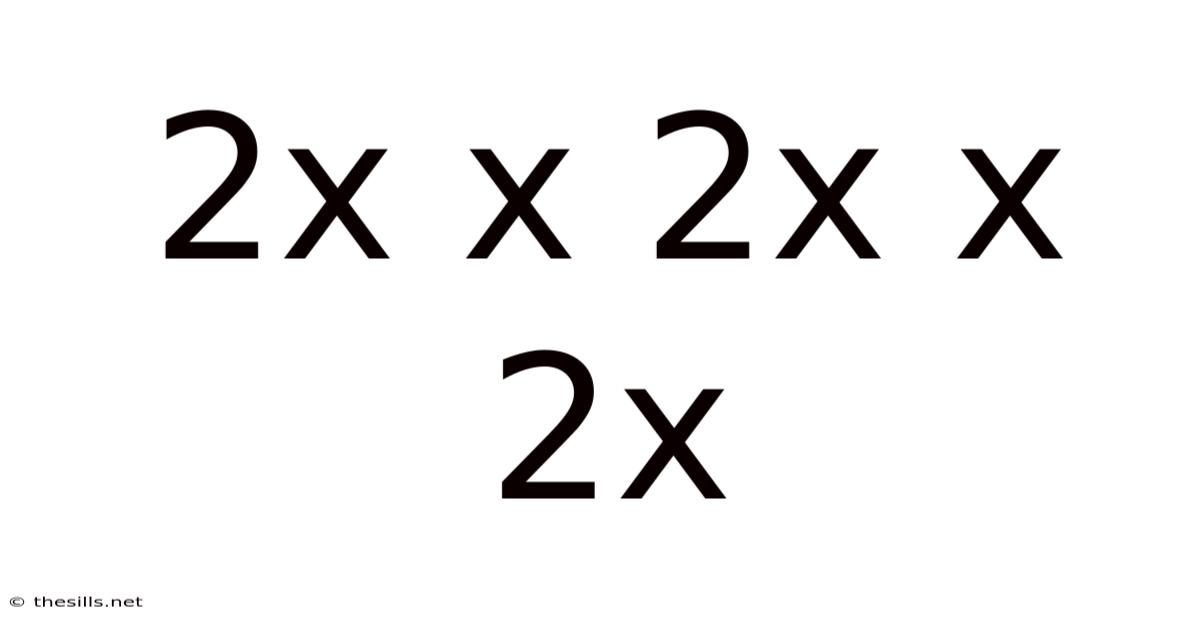
Table of Contents
Decoding 2x x 2x x 2x: Exploring Exponential Growth and its Real-World Applications
This article delves into the mathematical concept represented by "2x x 2x x 2x," exploring its meaning, implications, and applications across various fields. We'll unpack the concept of exponential growth, discuss its significance in understanding phenomena ranging from population dynamics to compound interest, and illustrate its power through real-world examples. Understanding this seemingly simple expression unlocks a deeper appreciation for the profound impact of exponential growth in shaping our world.
Understanding Exponential Growth: Beyond Linearity
At its core, "2x x 2x x 2x" represents a specific case of exponential growth. Unlike linear growth, where a quantity increases by a constant amount over time, exponential growth involves an increase by a constant factor or rate. In this instance, the factor is 2, and the expression signifies a repeated multiplication by 2, resulting in a much faster increase than linear growth. We can simplify this expression as 8x³, highlighting the cubic relationship between the initial value (x) and the final result.
Imagine starting with a single bacterium (x = 1). If it doubles every hour (2x), after three hours, you'd have 2 x 2 x 2 = 8 bacteria. This is a stark contrast to linear growth, where adding two bacteria per hour would result in only 7 bacteria after three hours. This seemingly small difference in growth rate escalates dramatically over time. The larger the initial value of 'x' and the longer the time period, the more pronounced the difference becomes between exponential and linear growth.
Dissecting the Expression: Mathematical Representation and Implications
Mathematically, "2x x 2x x 2x" can be simplified and generalized. Let's break down the process:
-
Simplification: 2x x 2x x 2x = 8x³. This shows that the final result is eight times the cube of the initial value.
-
Generalization: The expression can be generalized to represent exponential growth with a base 'a' and a time period 'n': a<sup>n</sup>x. In our case, a = 2 and n = 3. This generalized form allows us to model exponential growth with different bases and time periods. For example, a population growing at a rate of 3% annually can be modeled using a base of 1.03.
-
Significance of the Exponent: The exponent (3 in this case) represents the number of times the base (2) is multiplied by itself. This directly reflects the number of periods of growth. The larger the exponent, the greater the overall growth.
-
Understanding the impact of 'x': The value of 'x' significantly influences the final outcome. A larger initial value of 'x' leads to a much larger final result, even if the exponential growth rate remains the same.
Real-World Applications: Where Exponential Growth Matters
Exponential growth is not just a mathematical concept; it's a powerful tool for understanding and modeling various real-world phenomena. Here are a few examples:
1. Population Growth: The growth of human populations, animal populations, and even bacterial colonies often follows an exponential pattern, particularly when resources are abundant. Understanding exponential population growth is crucial for predicting future needs for resources like food, water, and housing, and for managing environmental impacts.
2. Compound Interest: One of the most widely recognized examples of exponential growth is compound interest. When interest is added to the principal amount, and subsequent interest is calculated on the accumulated amount, the growth becomes exponential. This concept is fundamental to understanding personal finance, investments, and economic growth. A small initial investment can grow substantially over time due to the power of compounding.
3. Technological Advancement: The advancement of technology often follows an exponential trajectory. Moore's Law, which observes the doubling of transistors on a microchip approximately every two years, is a classic example. This exponential growth in computing power has driven incredible advancements across various fields, from medicine to communication.
4. Viral Spread: The spread of infectious diseases, particularly viruses, often demonstrates exponential growth in the early stages of an outbreak. Understanding the exponential nature of viral spread is essential for public health officials to implement effective control measures and predict the trajectory of an epidemic.
5. Radioactive Decay: While we've primarily discussed exponential growth, the principle also applies to exponential decay. Radioactive decay, where the amount of a radioactive substance decreases over time, follows an exponential pattern. Understanding this pattern is crucial in fields like nuclear physics and medicine (e.g., using radioactive isotopes for medical imaging).
6. Chain Reactions: Exponential growth is also apparent in chain reactions, such as nuclear fission or even social phenomena like viral marketing. Each event triggers multiple subsequent events, leading to rapid escalation.
Beyond 2x x 2x x 2x: Exploring Variations and Limitations
While "2x x 2x x 2x" provides a clear illustration of exponential growth, it’s important to acknowledge the variations and limitations of this model:
-
Different Growth Rates: Exponential growth isn't always characterized by a doubling (base 2). The growth rate can vary depending on the phenomenon being modeled. The general formula a<sup>n</sup>x allows us to adapt the model to different growth rates.
-
Resource Limitations: In reality, exponential growth often faces limitations. Factors like resource scarcity, competition, or environmental constraints can prevent unlimited growth. Logistic growth models, which incorporate carrying capacity, are more realistic for many situations.
-
Unpredictability: While exponential growth models provide valuable insights, they are based on certain assumptions. External factors or unpredictable events can significantly alter the growth trajectory.
-
Long-Term Projections: Extrapolating exponential growth over extremely long periods can lead to unrealistic predictions. This highlights the importance of considering limitations and external factors when making long-term forecasts.
Frequently Asked Questions (FAQ)
Q: What is the difference between linear and exponential growth?
A: Linear growth increases by a constant amount over time, while exponential growth increases by a constant factor or rate. Exponential growth results in much faster increases, especially over longer periods.
Q: How can I calculate exponential growth?
A: The general formula for exponential growth is a<sup>n</sup>x, where 'a' is the growth factor, 'n' is the number of periods, and 'x' is the initial value.
Q: What are some real-world limitations of exponential growth models?
A: Real-world limitations include resource scarcity, competition, environmental constraints, and unpredictable events. These factors can prevent unlimited exponential growth.
Conclusion: The Power and Perils of Exponential Growth
The expression "2x x 2x x 2x," while seemingly simple, encapsulates a profound mathematical concept with far-reaching applications. Understanding exponential growth is crucial for comprehending a wide range of phenomena, from population dynamics to technological advancements. While the power of exponential growth can be harnessed for positive outcomes (e.g., economic growth, technological progress), it's equally important to recognize its limitations and potential downsides (e.g., unsustainable population growth, resource depletion). By understanding both the power and the perils, we can better prepare for the future and make informed decisions based on the realities of exponential growth in our world. It’s a concept that demands our attention and understanding, impacting virtually every aspect of our lives.
Latest Posts
Latest Posts
-
2x 2 X 6 Factored
Sep 13, 2025
-
Picture Of A Hydrogen Bomb
Sep 13, 2025
-
A 1 A 2 0
Sep 13, 2025
-
How Much Is 1 Amu
Sep 13, 2025
-
Magnitude Of The Electric Force
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2x X 2x X 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.