2x 2 X 6 Factored
thesills
Sep 13, 2025 · 5 min read
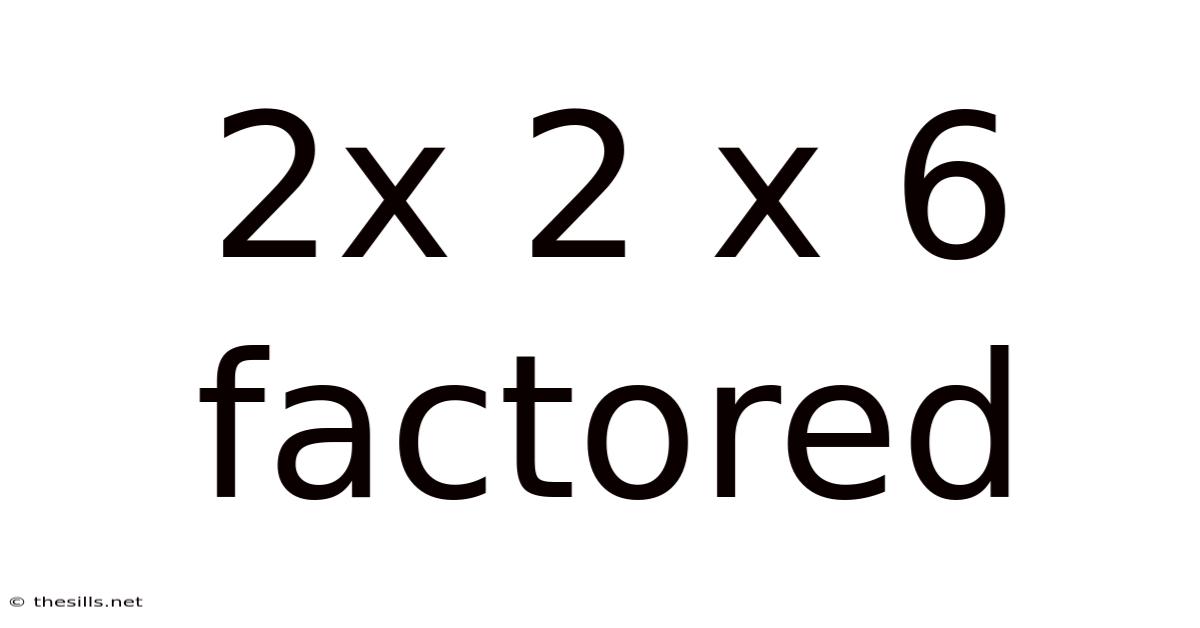
Table of Contents
Exploring the Factorization of 2 x 2 x 6: A Deep Dive into Prime Numbers and Composite Numbers
Understanding the factorization of numbers is fundamental to mathematics. This article delves into the factorization of 2 x 2 x 6, exploring the concepts of prime numbers, composite numbers, and the prime factorization theorem. We'll unpack the process step-by-step, making it accessible to learners of all levels, while also touching upon more advanced concepts for those seeking a deeper understanding. This exploration will also cover common questions and misconceptions surrounding factorization.
Introduction: What is Factorization?
Factorization, also known as prime factorization, is the process of breaking down a composite number into its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11). A composite number, on the other hand, is a whole number greater than 1 that can be divided evenly by numbers other than 1 and itself (e.g., 4, 6, 9, 12). The expression "2 x 2 x 6" represents a composite number expressed as a product of its factors. Our goal is to determine the prime factorization of this number.
Step-by-Step Factorization of 2 x 2 x 6
The expression 2 x 2 x 6 already provides us with a factorization, but it's not the prime factorization. To achieve prime factorization, we need to ensure that all the factors are prime numbers. Let's break it down:
-
Identify the Factors: We begin with the given factors: 2, 2, and 6.
-
Check for Prime Factors: The numbers 2 and 2 are already prime numbers. However, 6 is a composite number.
-
Factor the Composite Number: We need to find the prime factors of 6. 6 can be factored into 2 x 3. Both 2 and 3 are prime numbers.
-
Complete Prime Factorization: Now, we substitute the prime factors of 6 (2 and 3) into the original expression: 2 x 2 x 2 x 3.
-
Simplify (Optional): We can simplify this expression by grouping like factors: 2³ x 3. This signifies that the number is composed of three factors of 2 and one factor of 3.
Therefore, the prime factorization of 2 x 2 x 6 is 2³ x 3 or 2 x 2 x 2 x 3. This means the original number, which is 24 (2 x 2 x 6 = 24), is solely composed of the prime factors 2 and 3.
The Fundamental Theorem of Arithmetic
The process we just followed is a direct application of the Fundamental Theorem of Arithmetic, also known as the Unique Prime Factorization Theorem. This theorem states that every integer greater than 1 can be represented as a product of prime numbers in a unique way, except for the order of the factors. This theorem is a cornerstone of number theory and is crucial for many mathematical concepts.
Understanding Prime Factorization: Beyond the Calculation
While the calculation itself is straightforward, understanding the significance of prime factorization extends far beyond simply finding the prime factors of a number. Let's explore some key applications:
-
Greatest Common Divisor (GCD) and Least Common Multiple (LCM): Prime factorization is essential for efficiently calculating the GCD and LCM of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder, while the LCM is the smallest number that is a multiple of all the given numbers. By finding the prime factorization of each number, we can easily identify common factors and determine the GCD and LCM.
-
Simplifying Fractions: Prime factorization is instrumental in simplifying fractions to their lowest terms. By factoring the numerator and denominator, we can cancel out common factors, resulting in a simpler, equivalent fraction.
-
Solving Algebraic Equations: Factorization is a crucial technique in solving various algebraic equations. By factoring expressions, we can find the roots or solutions of equations.
-
Cryptography: Prime numbers play a critical role in modern cryptography, particularly in public-key cryptography systems such as RSA. The security of these systems relies on the difficulty of factoring very large composite numbers into their prime factors.
-
Number Theory Research: Prime factorization is a central concept in advanced number theory research, leading to many unsolved problems and ongoing research areas. For example, understanding the distribution of prime numbers is a significant challenge with profound implications.
Common Mistakes and Misconceptions
Several common mistakes can arise when working with prime factorization:
-
Failing to Identify All Prime Factors: Students may sometimes stop factoring before reaching all the prime factors. It’s crucial to ensure that all factors are indeed prime.
-
Incorrectly Identifying Prime Numbers: A common mistake is incorrectly identifying composite numbers as prime numbers or vice-versa. Understanding the definition of prime and composite numbers is paramount.
-
Not Simplifying the Result: While not mathematically incorrect, leaving the prime factorization in an unsimplified form makes it harder to understand and use in further calculations. Simplifying the result using exponents makes the representation more concise and efficient.
Frequently Asked Questions (FAQ)
-
Q: Is there only one prime factorization for a given number?
- A: Yes, according to the Fundamental Theorem of Arithmetic, every composite number has a unique prime factorization (ignoring the order of the factors).
-
Q: How do I find the prime factorization of a larger number?
- A: For larger numbers, you can use a combination of techniques, such as trial division (dividing by progressively larger prime numbers) or factorization algorithms. These algorithms are often implemented in computer programs for efficient factorization of very large numbers.
-
Q: What is the significance of prime factorization in real-world applications?
- A: Prime factorization has wide-ranging applications in cryptography, coding theory, and other fields requiring secure data transmission and processing.
Conclusion: The Power of Prime Factorization
The factorization of 2 x 2 x 6, resulting in 2³ x 3, is a simple yet powerful demonstration of a fundamental mathematical concept. Prime factorization is not merely an abstract mathematical exercise; it’s a crucial tool with broad applications across various fields. Understanding prime factorization enhances mathematical skills, provides a pathway to more advanced concepts, and reveals the inherent structure and elegance within the seemingly simple world of numbers. From simplifying fractions to securing online transactions, the seemingly simple process of breaking down a number into its prime constituents holds immense power and practical value. By mastering this foundational concept, we unlock the door to a deeper understanding of the fascinating world of mathematics.
Latest Posts
Latest Posts
-
14k Gold Jewelry Making Kit
Sep 13, 2025
-
As Disposable Income Increases Consumption
Sep 13, 2025
-
The Year Of The Book
Sep 13, 2025
-
Integral Of 1 1 Tanx
Sep 13, 2025
-
Potassium Hydroxide And Sodium Hydroxide
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2x 2 X 6 Factored . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.