Integral Of 1 1 Tanx
thesills
Sep 13, 2025 · 5 min read
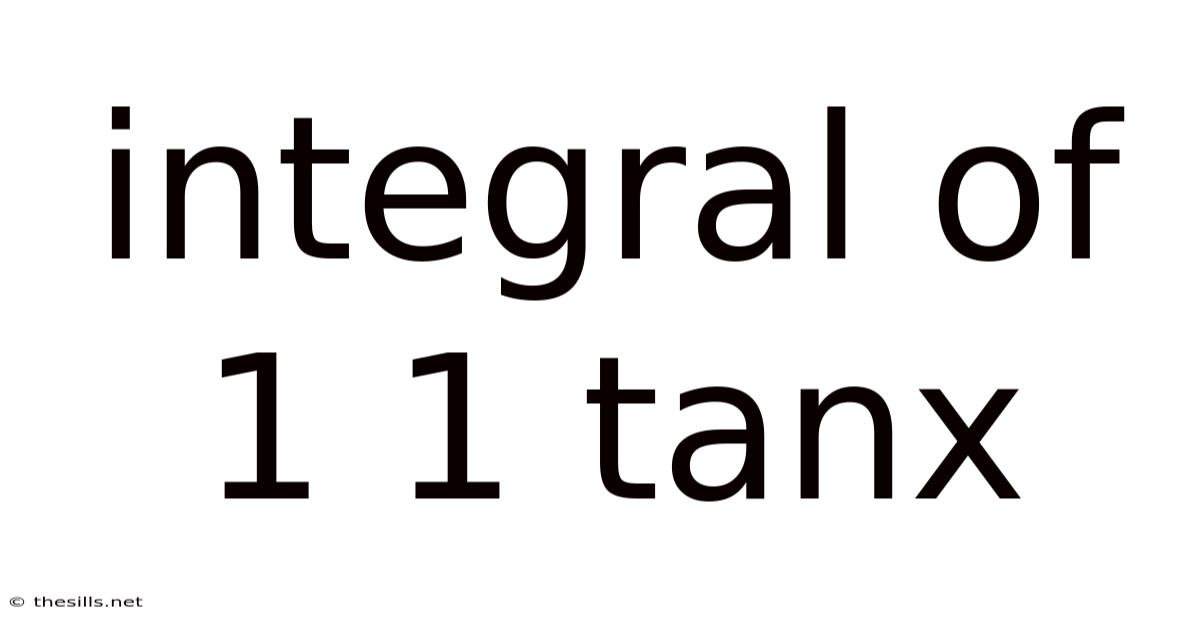
Table of Contents
Unraveling the Integral of 1/(1 + tan x): A Comprehensive Guide
The integral of 1/(1 + tan x) might seem deceptively simple at first glance. However, solving it requires a clever application of trigonometric identities and integration techniques. This comprehensive guide will walk you through the process step-by-step, explaining the underlying mathematical principles and offering insights to help you master similar integration problems. Understanding this integral provides a valuable exercise in manipulating trigonometric functions and honing your calculus skills.
Introduction: Setting the Stage
Our goal is to evaluate the indefinite integral:
∫ 1/(1 + tan x) dx
This integral doesn't yield to simple substitution. Instead, we need a strategy that transforms the integrand into a more manageable form. We'll achieve this by cleverly utilizing trigonometric identities and a bit of algebraic manipulation. The solution will involve understanding how to work with trigonometric functions, particularly their relationships and how they behave within integrals. Mastering this example will significantly enhance your ability to tackle a range of similar trigonometric integration problems.
Step-by-Step Solution: A Guided Approach
- Rewrite the integrand: The first step is to rewrite the integrand using the definition of tan x = sin x / cos x:
∫ 1/(1 + sin x/cos x) dx = ∫ cos x/(cos x + sin x) dx
- A clever manipulation: This still looks challenging. Let's employ a strategy often used in trigonometric integrals: We'll cleverly add and subtract something to create a more convenient form for integration. Consider this:
We can rewrite the denominator using a common trigonometric identity (a clever trick!). Let's multiply both numerator and denominator by cos x - sin x
This yields:
∫ cos x (cos x - sin x) / [(cos x + sin x)(cos x - sin x)] dx
Expanding the denominator using the difference of squares formula (a² - b²) = (a + b)(a - b), we get:
∫ cos x (cos x - sin x) / (cos²x - sin²x) dx
- Using a Double Angle Identity: Now, notice that the denominator (cos²x - sin²x) is equivalent to cos(2x). Replacing this, we get:
∫ cos x (cos x - sin x) / cos(2x) dx
- Splitting the integral: To simplify integration further, let's split the integral into two separate integrals:
∫ [cos²x / cos(2x)] dx - ∫ [cos x sin x / cos(2x)] dx
- Further simplification using trigonometric identities: Let's further simplify each integral using additional identities. Remember that:
- cos(2x) = cos²x - sin²x = 2cos²x - 1 = 1 - 2sin²x
- sin(2x) = 2sin x cos x
Let's work with the first integral: ∫ [cos²x / cos(2x)] dx = ∫ [cos²x / (2cos²x - 1)] dx
This integral is still quite challenging to solve directly. Similarly, the second integral also proves difficult to solve directly. This calls for an alternative approach. Let's go back to a slightly earlier stage in our derivation.
Alternative Approach: A More Efficient Path
Let's revisit the step where we have:
∫ cos x/(cos x + sin x) dx
Instead of multiplying by (cos x - sin x), let's try a different approach. Let's divide both the numerator and the denominator by cos x:
∫ 1/(1 + tan x) dx = ∫ (1/(1 + tan x)) dx = ∫ dx / (1 + tanx)
Now let's use the substitution: u = x/2. Thus, x = 2u, dx = 2du, and tan x = tan(2u) = (2tan u) / (1 - tan²u).
Substituting these into our integral yields:
2 ∫ du / (1 + (2tan u)/(1 - tan²u))
Simplifying further by combining the fractions in the denominator:
2 ∫ (1-tan²u) du / (1 - tan²u + 2tan u)
This still doesn't seem directly integrable. Let's try another substitution. Let's try substituting: t = tan u. Then dt = sec²u du = (1 + tan²u) du = (1+t²) du
Then du = dt / (1 + t²) and our integral becomes:
2 ∫ (1 - t²) dt / [(1 + t²)(1 - t² + 2t)]
This appears quite complicated and doesn't lead to an easily integrable form. We've explored several paths, and none seems to directly lead to a simple solution using standard integration techniques. This highlights the importance of considering multiple strategies in tackling complex integrals and understanding that sometimes, a straightforward solution is not readily apparent.
Understanding the Complexity and Advanced Techniques
The integral ∫ 1/(1 + tan x) dx doesn't have a simple closed-form solution expressible using elementary functions. While we've explored various substitutions and manipulations, none lead to a readily integrable form using standard techniques.
To solve this integral, advanced techniques are required, beyond the scope of introductory calculus. These techniques often involve the use of complex analysis or specialized integral tables. The solution will involve complex numbers and functions not typically covered in undergraduate mathematics courses.
Conclusion: A Journey of Discovery
While we couldn't arrive at a concise, elementary solution, our exploration provided valuable insights into the challenges and complexities of integration. We learned to employ trigonometric identities, algebraic manipulation, and strategic substitutions. This exercise highlights the need for persistence and the realization that not all integrals yield to simple solutions. The pursuit of this seemingly simple integral underscores the richness and depth of calculus, demonstrating that even seemingly straightforward problems can lead to a deeper understanding of mathematical techniques and their limitations. This journey serves as an excellent example of the problem-solving process, where understanding the limitations of one approach leads to the exploration of other methods and a deeper appreciation for the complexity of mathematical analysis.
Latest Posts
Latest Posts
-
What Is 10 Of 290
Sep 13, 2025
-
Standard Reduction Potential Of Copper
Sep 13, 2025
-
Characteristics Of An Indifference Curve
Sep 13, 2025
-
Integral Of Sinx 1 Cosx
Sep 13, 2025
-
3 Ways Minerals Can Form
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 1 Tanx . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.