What Is 3x Times 2x
thesills
Sep 18, 2025 · 5 min read
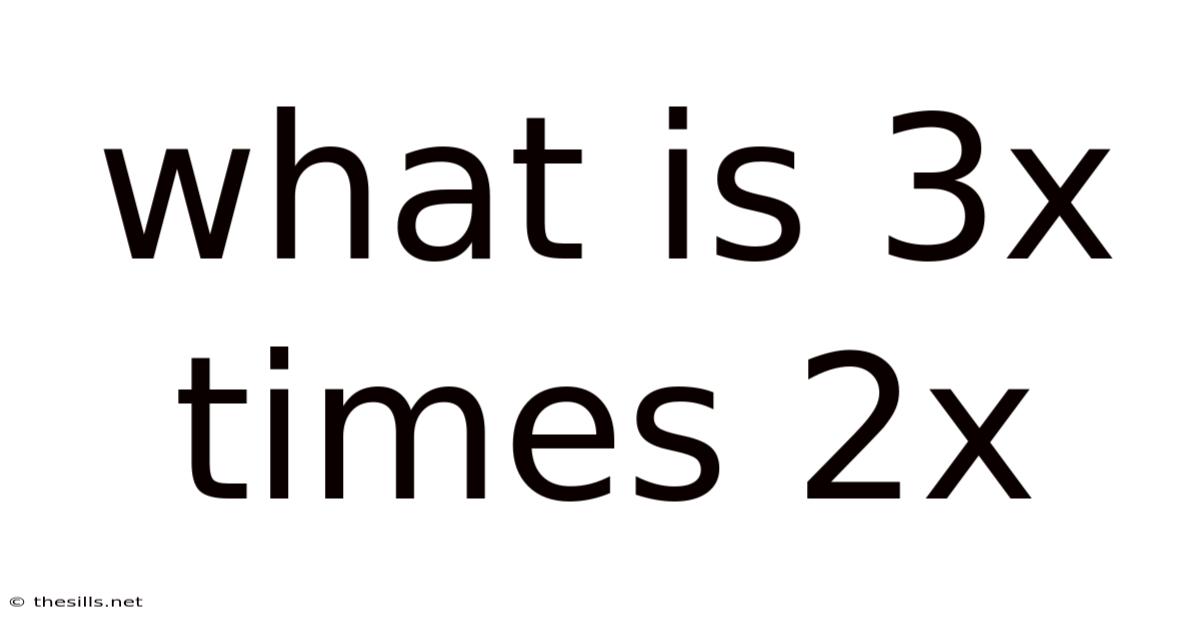
Table of Contents
Decoding the Mystery: What is 3x Times 2x? A Deep Dive into Algebraic Multiplication
This article explores the seemingly simple yet fundamentally important algebraic expression: 3x times 2x. Understanding this calculation is crucial for mastering fundamental algebra, a cornerstone of mathematics and a vital skill for numerous fields, from engineering to finance. We'll delve into the process, explain the underlying principles, and explore related concepts to build a strong foundation in algebraic manipulation.
Introduction: Understanding Variables and Coefficients
Before tackling 3x times 2x, let's refresh our understanding of basic algebraic components. In this expression, 'x' represents a variable, an unknown quantity that can take on different numerical values. The numbers '3' and '2' are coefficients, which are constants multiplying the variable. Therefore, 3x means "3 times x," and 2x means "2 times x."
The core of this problem involves understanding how to multiply terms containing variables. This process involves multiplying the coefficients and then dealing with the variables separately.
Step-by-Step Solution: Multiplying 3x and 2x
To solve 3x times 2x, we follow these simple steps:
-
Multiply the coefficients: Multiply the numerical coefficients together: 3 * 2 = 6.
-
Multiply the variables: Multiply the variables together: x * x = x². Remember, multiplying a variable by itself is equivalent to raising it to the power of 2 (x² is shorthand for x * x).
-
Combine the results: Combine the results from steps 1 and 2 to obtain the final answer: 6x².
Therefore, 3x times 2x equals 6x².
The Underlying Principles: The Distributive Property and Exponents
The solution above relies on two fundamental algebraic principles: the distributive property and the rules of exponents.
The Distributive Property: This property states that multiplying a sum (or difference) by a number is the same as multiplying each term in the sum (or difference) by that number and then adding (or subtracting) the results. While we don't have a sum or difference directly in 3x times 2x, understanding the distributive property lays the groundwork for more complex algebraic manipulations. For example, if we had (3x + 2) * 2x, we would use the distributive property: 2x * 3x + 2x * 2, which simplifies to 6x² + 4x.
Rules of Exponents: The multiplication of variables (x * x = x²) follows the rules of exponents. Specifically, when multiplying terms with the same base (in this case, 'x'), we add the exponents. Since x can be written as x¹, then x¹ * x¹ = x⁽¹⁺¹⁾ = x². This rule extends to more complex expressions. For instance, x² * x³ = x⁽²⁺³⁾ = x⁵. Understanding exponent rules is paramount for advanced algebraic calculations.
Expanding the Concept: More Complex Examples
Let's expand our understanding by looking at more complex examples that build upon the core principle of multiplying terms with variables:
-
(4x)(5y): Here, we have different variables (x and y). We multiply the coefficients: 4 * 5 = 20. Then we multiply the variables: x * y = xy. The result is 20xy. Note that we cannot simplify xy further because they are different variables.
-
(2x²)(3x³): This involves multiplying terms with both coefficients and exponents. We multiply the coefficients: 2 * 3 = 6. Then we multiply the variables: x² * x³ = x⁽²⁺³⁾ = x⁵. The final result is 6x⁵.
-
(-2x)(4x): This example introduces a negative coefficient. We multiply the coefficients: -2 * 4 = -8. The variable multiplication remains the same: x * x = x². The result is -8x².
Practical Applications: Where You'll Use This Knowledge
The ability to multiply algebraic terms like 3x and 2x is a fundamental skill with extensive applications in various fields:
-
Solving Equations: Many algebraic equations require simplifying expressions by multiplying variables. For instance, solving the equation 3x = 6 involves dividing both sides by 3. However, understanding how to multiply terms is crucial for manipulating more complex equations.
-
Geometry and Area Calculations: Calculating the area of a rectangle involves multiplying its length and width. If the length is represented by 3x and the width by 2x, finding the area requires multiplying 3x and 2x, resulting in 6x².
-
Physics and Engineering: Many physical phenomena are modeled using algebraic equations involving variables. Understanding how to manipulate these expressions is essential for solving problems in various branches of physics and engineering.
-
Finance and Economics: Financial modeling often involves algebraic equations that describe relationships between various financial variables. The ability to multiply terms involving variables is crucial for making accurate predictions and informed decisions.
Frequently Asked Questions (FAQ)
Q: What if I have more than two terms to multiply?
A: If you have more than two terms, multiply them step-by-step. For instance, (2x)(3x)(4x) would be solved as: (2x)(3x) = 6x², then (6x²)(4x) = 24x³.
Q: Can I multiply different variables?
A: Yes, absolutely. You simply multiply the coefficients and then write the variables next to each other. For example, (2x)(3y) = 6xy.
Q: What happens if one of the terms is zero?
A: If any of the terms is zero, the entire product will be zero. This is because anything multiplied by zero equals zero.
Q: What if x is a specific number? How would this calculation change?
A: If 'x' is a specific number, you substitute that value into the expression 6x² after you've simplified it. For example, if x = 2, then 6x² = 6(2)² = 6 * 4 = 24.
Conclusion: Mastering the Fundamentals
Understanding how to multiply algebraic terms such as 3x times 2x is a cornerstone of algebraic proficiency. It builds upon fundamental principles like the distributive property and the rules of exponents, paving the way for tackling more complex algebraic manipulations and solving problems in various fields. By mastering this concept, you'll significantly improve your mathematical skills and unlock a deeper understanding of the world around us. Remember to practice regularly, and don't hesitate to explore further related topics like factoring and polynomial expansion to build a robust understanding of algebra.
Latest Posts
Latest Posts
-
2 Chloro 4 Methyl Pentane
Sep 18, 2025
-
Difference Between Shears And Scissors
Sep 18, 2025
-
Derivative Of Sec X Tanx
Sep 18, 2025
-
Functional Groups In Ascorbic Acid
Sep 18, 2025
-
Do Chickens Have Bone Marrow
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 3x Times 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.