What Is 30 Of 89
thesills
Sep 13, 2025 · 6 min read
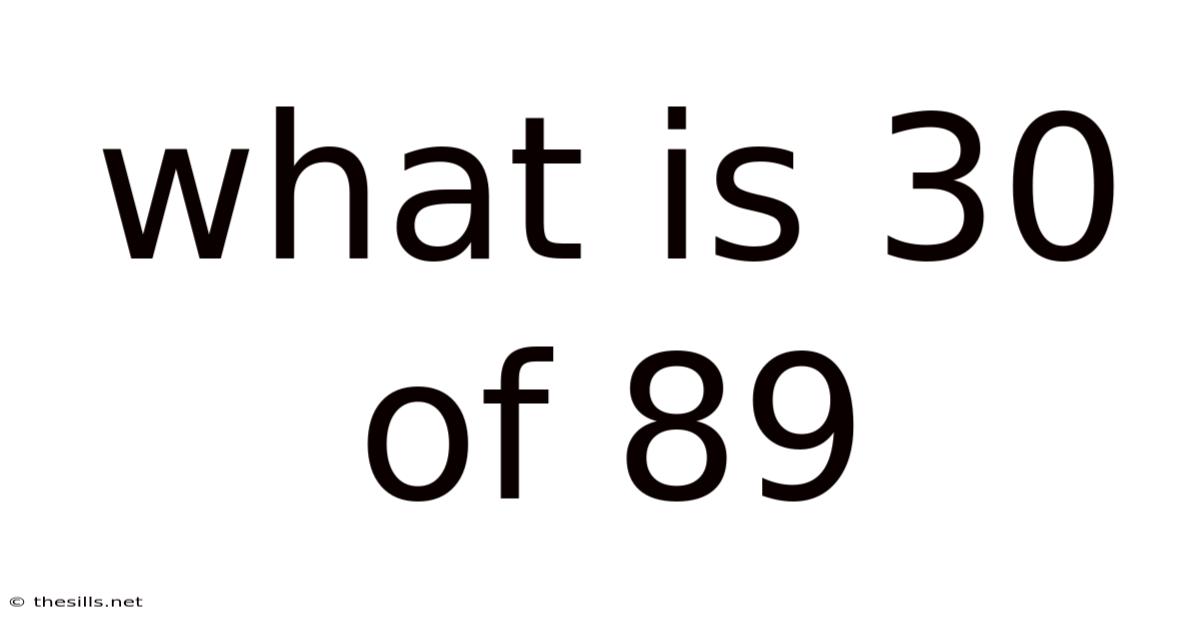
Table of Contents
What is 30 of 89? Unpacking Fractions, Percentages, and Decimals
What is 30 of 89? This seemingly simple question opens the door to a deeper understanding of fundamental mathematical concepts: fractions, percentages, and decimals. While a calculator can quickly provide the answer, exploring the how behind the calculation offers valuable insights into mathematical reasoning and problem-solving skills. This article will delve into the various ways to interpret and solve this problem, providing a comprehensive explanation suitable for students and anyone looking to refresh their math skills.
Understanding the Question: Fractions as a Starting Point
The phrase "30 of 89" inherently represents a fraction. In mathematical terms, we can express this as 30/89. This fraction indicates that we are considering 30 parts out of a total of 89 parts. Understanding fractions is crucial for grasping the essence of this problem. A fraction always consists of two parts: the numerator (the top number, representing the portion we're interested in) and the denominator (the bottom number, representing the whole). In this case, 30 is the numerator and 89 is the denominator.
Calculating the Decimal Equivalent
To obtain a decimal representation of 30/89, we perform a simple division: 30 divided by 89. Using a calculator or long division, we find that:
30 ÷ 89 ≈ 0.337
This means that 30 out of 89 represents approximately 0.337. This decimal value provides a more readily understandable representation for many applications. It tells us that 30 is roughly one-third of 89.
Converting to a Percentage
Percentages offer another perspective on the relationship between 30 and 89. To convert the decimal 0.337 to a percentage, we simply multiply by 100:
0.337 x 100 ≈ 33.7%
Therefore, 30 is approximately 33.7% of 89. This percentage representation is widely used to express proportions and ratios in various contexts, making it easier to compare and interpret results.
Long Division: A Step-by-Step Approach
For those who prefer a manual calculation, let's explore long division to find the decimal equivalent of 30/89.
-
Set up the long division: Place 30 inside the division symbol (the long division bracket) and 89 outside.
-
Add a decimal point and zeros: Add a decimal point after the 30 and as many zeros as needed to continue the division process.
-
Begin the division: Since 89 doesn't go into 30, we add a zero and a decimal point to the quotient (the answer). We now consider 300. 89 goes into 300 three times (89 x 3 = 267). Write 3 above the decimal point in the quotient.
-
Subtract and bring down: Subtract 267 from 300, which leaves 33. Bring down the next zero to make 330.
-
Repeat the process: 89 goes into 330 three times (89 x 3 = 267). Write 3 in the quotient.
-
Continue until desired accuracy: Subtract 267 from 330, leaving 63. Bring down another zero to make 630. Continue this process until you reach the desired level of accuracy. You'll find the decimal value will continue to extend, approaching but never quite reaching a perfectly terminating decimal.
This long division method demonstrates the underlying principle of converting a fraction into a decimal. While calculators provide quick answers, understanding the process enriches your mathematical intuition.
Real-World Applications: Why This Matters
Understanding how to calculate "30 of 89" extends far beyond simple arithmetic. It's a fundamental skill applied across numerous fields:
-
Statistics and Probability: Calculating proportions, percentages, and probabilities in statistical analysis relies heavily on the ability to work with fractions and decimals.
-
Finance: Calculating interest rates, discounts, and profit margins all involve working with fractions and percentages. Understanding these concepts is vital for financial literacy and decision-making.
-
Science: Many scientific measurements and calculations use ratios and proportions, directly related to the concepts demonstrated in this problem.
-
Engineering: Similar to science, engineering heavily relies on precise calculations, requiring a thorough understanding of fractions, decimals, and percentages to ensure accuracy and safety.
-
Everyday Life: From calculating tips in restaurants to understanding sales discounts, the ability to quickly estimate fractions and percentages is incredibly valuable in daily life.
Expanding on the Concept: Proportions and Ratios
The problem "30 of 89" can also be viewed through the lens of proportions and ratios. A ratio compares two quantities, often expressed as a fraction. In this case, the ratio of 30 to 89 can be written as 30:89 or 30/89.
A proportion is a statement of equality between two ratios. We can use proportions to solve related problems. For instance, if we wanted to find out what number is 30% of 178, we could set up the proportion:
30/100 = x/178
Solving for x, we find that x ≈ 53.4. This demonstrates how understanding proportions and ratios allows us to solve similar problems, scaling the initial relationship to different contexts.
Frequently Asked Questions (FAQ)
Q1: Is there a way to simplify the fraction 30/89?
A1: No, the fraction 30/89 is already in its simplest form. Both the numerator (30) and the denominator (89) do not share any common factors other than 1.
Q2: How accurate is the approximation 0.337?
A2: The accuracy depends on the context. The approximation 0.337 is a truncation of a non-terminating decimal. To increase accuracy, more decimal places can be calculated using long division or a calculator. For most practical purposes, 0.337 offers sufficient accuracy.
Q3: Can I use a different method to calculate the percentage?
A3: Yes, you can calculate the percentage by first finding the decimal value (30/89 ≈ 0.337) and then multiplying by 100, as described above. Alternatively, you can directly calculate (30/89) * 100% using a calculator to get the percentage directly.
Q4: What if I need to express this as a mixed number?
A4: Since the numerator (30) is smaller than the denominator (89), 30/89 cannot be expressed as a mixed number. Mixed numbers are used to represent improper fractions (where the numerator is larger than the denominator).
Conclusion: Beyond the Answer
The seemingly straightforward question "What is 30 of 89?" serves as a gateway to a more profound understanding of fractions, decimals, percentages, ratios, and proportions. While a calculator provides a quick numerical answer, the journey of understanding the underlying mathematical concepts is far more valuable. This comprehensive exploration emphasizes the importance of mastering these fundamental skills, equipping individuals with the ability to confidently tackle similar problems across diverse fields and daily life scenarios. The ability to dissect and comprehend these fundamental mathematical concepts forms a solid foundation for further mathematical learning and problem-solving abilities. Remember, the value lies not just in getting the answer, but in understanding the process.
Latest Posts
Latest Posts
-
What Was The Question Again
Sep 13, 2025
-
7 2 X 1 2
Sep 13, 2025
-
Aim Or Group Of Party
Sep 13, 2025
-
Ventral Blood Vessel In Earthworm
Sep 13, 2025
-
Weight Is Vector Or Scalar
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 89 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.