What Fraction Is 20 Percent
thesills
Sep 14, 2025 · 5 min read
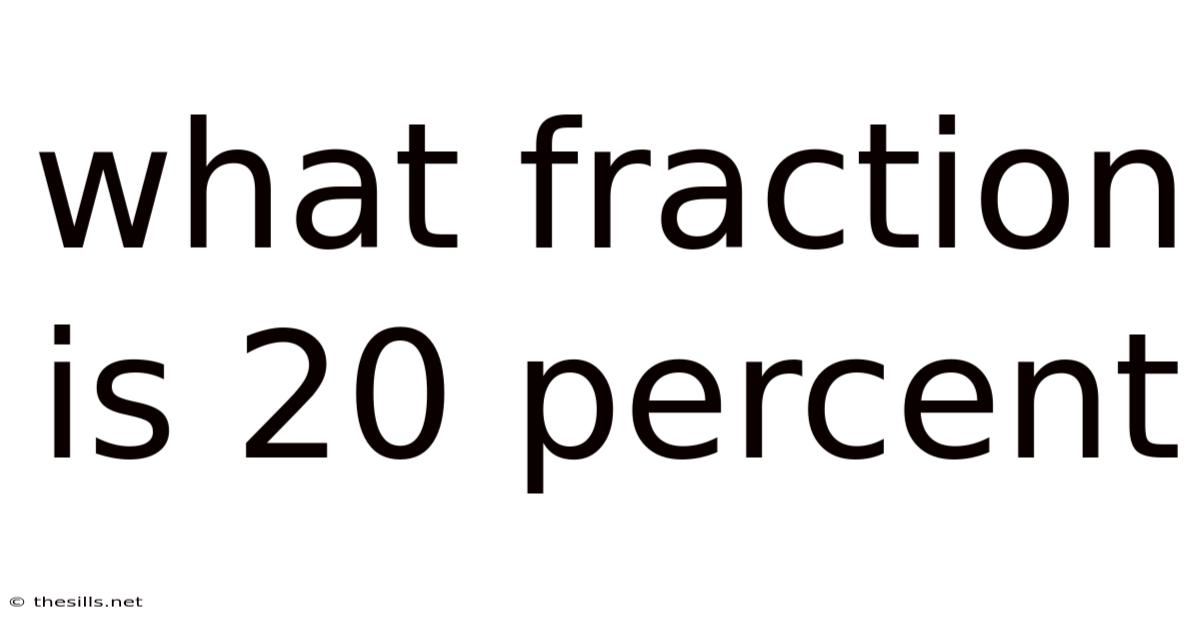
Table of Contents
What Fraction is 20 Percent? A Deep Dive into Percentages and Fractions
Understanding the relationship between percentages and fractions is a fundamental skill in mathematics with applications spanning various fields, from basic arithmetic to advanced finance. This comprehensive guide will explore the conversion of percentages to fractions, focusing specifically on the question: what fraction is 20 percent? We'll delve into the underlying principles, provide step-by-step instructions, and address common misconceptions to solidify your understanding. This article will equip you with the knowledge to confidently tackle similar percentage-to-fraction conversions.
Understanding Percentages and Fractions
Before we tackle the specific problem, let's review the definitions of percentages and fractions. A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" ("per" meaning "for each" and "cent" meaning "hundred"). We represent percentages using the "%" symbol.
A fraction, on the other hand, represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
The connection between percentages and fractions lies in the fact that a percentage can always be written as a fraction with a denominator of 100. This is the key to converting between the two.
Converting 20 Percent to a Fraction: A Step-by-Step Guide
Now, let's address the central question: what fraction is 20 percent?
Step 1: Write the percentage as a fraction with a denominator of 100.
20% can be written as 20/100. This is because the definition of percentage implies "out of 100".
Step 2: Simplify the fraction.
The fraction 20/100 is not in its simplest form. To simplify, we find the greatest common divisor (GCD) of the numerator and denominator. The GCD of 20 and 100 is 20. We divide both the numerator and the denominator by the GCD:
20 ÷ 20 = 1 100 ÷ 20 = 5
Therefore, the simplified fraction is 1/5.
Conclusion: 20 percent is equal to the fraction 1/5.
Visualizing the Conversion
Imagine a pizza cut into 100 equal slices. 20% of the pizza represents 20 of those slices. If you group those 20 slices into sets of 20, you'll have one group out of a total of five groups (100 slices / 20 slices per group = 5 groups). This visually represents the simplification from 20/100 to 1/5.
Different Approaches to Percentage to Fraction Conversion
While the method above is the most straightforward, there are other approaches to converting percentages to fractions. Let's explore a few:
-
Using decimal representation: You can first convert the percentage to a decimal by dividing by 100. 20% becomes 0.20. Then, you can write this decimal as a fraction: 0.20 = 20/100. This fraction can then be simplified as shown in the previous example.
-
Direct simplification: Some students might intuitively see that 20 is one-fifth of 100 (100/20 = 5). This immediately leads to the fraction 1/5. This approach works well for percentages that are simple fractions of 100.
Expanding the Understanding: Working with Other Percentages
The principles discussed above can be applied to convert any percentage into a fraction. Let's look at a few more examples:
- 50%: 50/100 simplifies to 1/2.
- 75%: 75/100 simplifies to 3/4.
- 33.33...% (approximately): 33.33.../100 approximates to 1/3 (Note: this is a recurring decimal and a perfectly precise fractional representation requires understanding recurring decimals)
- 12.5%: 12.5/100 = 125/1000 simplifies to 1/8
Practical Applications of Percentage to Fraction Conversion
The ability to convert percentages to fractions is crucial in many real-world scenarios:
-
Calculating discounts: If a store offers a 20% discount, you can easily calculate the discount amount by multiplying the original price by 1/5.
-
Determining proportions: Fractions are often easier to work with when dealing with proportions and ratios. Converting percentages to fractions can simplify such calculations.
-
Understanding data representation: Many statistical representations use fractions to illustrate data relationships. Converting percentages to fractions allows for a better understanding of this data.
-
Solving mathematical problems: Many mathematical word problems involve percentages and fractions. Converting between these formats is essential for solving such problems.
Frequently Asked Questions (FAQ)
Q1: Can all percentages be expressed as simple fractions?
A1: No, not all percentages can be expressed as simple fractions. Percentages like 1/3 (approximately 33.33%) result in repeating decimals and require understanding of recurring decimals or the use of approximate fractions.
Q2: What if the percentage is a decimal, like 20.5%?
A2: You would treat it the same way. 20.5% is 20.5/100. To simplify, you can multiply the numerator and denominator by 10 to remove the decimal: 205/1000. Then simplify by finding the GCD which is 5: 41/200.
Q3: Why is simplifying fractions important?
A3: Simplifying fractions makes them easier to understand and work with. A simplified fraction provides the most concise representation of the ratio.
Q4: Are there any online tools to help with percentage to fraction conversions?
A4: Yes, many online calculators and converters are readily available to perform this conversion. However, understanding the underlying process is key for problem-solving and further mathematical development.
Conclusion
Converting percentages to fractions is a fundamental mathematical skill. By understanding the relationship between percentages and fractions, and by applying the simple steps outlined in this guide, you can confidently convert any percentage into its fractional equivalent. The ability to perform this conversion is not only valuable for academic success but also essential for navigating numerous real-world applications requiring a deep understanding of proportions, ratios, and data interpretation. Remember, mastering this skill builds a strong foundation for more advanced mathematical concepts. Practice various examples, and don't hesitate to explore additional resources to further enhance your understanding.
Latest Posts
Latest Posts
-
X3 Cos X 2 1 2
Sep 14, 2025
-
Acoelomate Vs Pseudocoelomate Vs Coelomate
Sep 14, 2025
-
3 Protons And 4 Neutrons
Sep 14, 2025
-
Square Root Of 448 Simplified
Sep 14, 2025
-
What Shapes Have Perpendicular Sides
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Fraction Is 20 Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.