X3 Cos X/2 + 1/2
thesills
Sep 14, 2025 · 6 min read
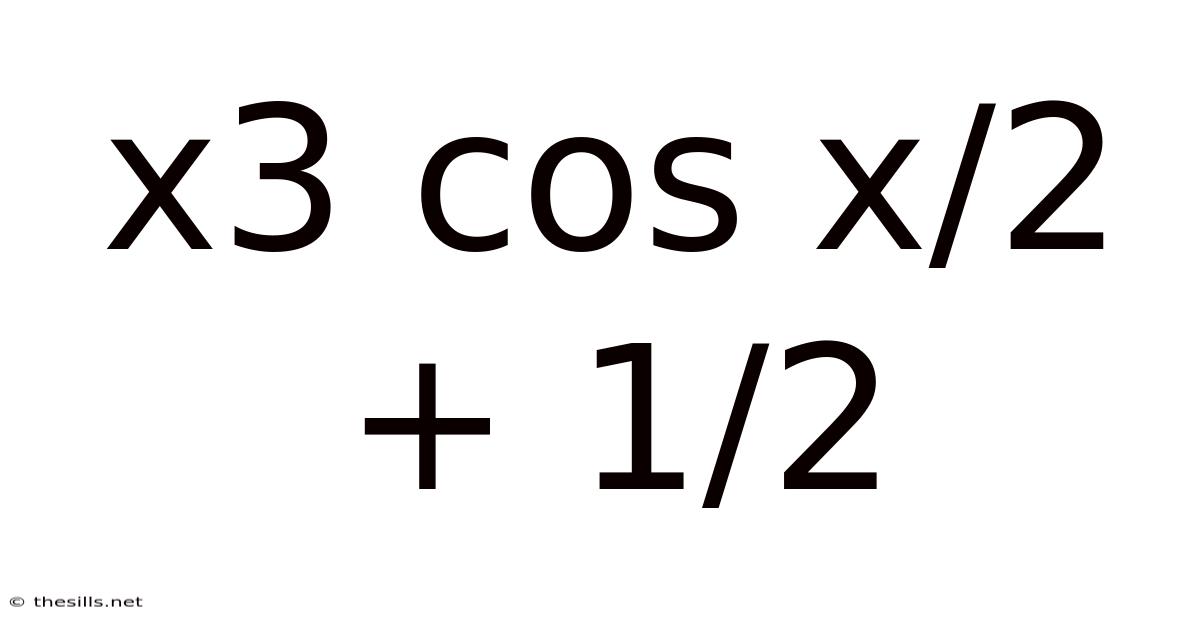
Table of Contents
Exploring the Mathematical Landscape of x³cos(x/2) + 1/2: A Deep Dive
This article delves into the fascinating mathematical expression x³cos(x/2) + 1/2, exploring its properties, behavior, and potential applications. We'll dissect its components, analyze its graphical representation, investigate its derivatives and integrals, and consider its relevance within broader mathematical contexts. Understanding this seemingly simple expression reveals a surprising depth, showcasing the interplay between polynomial and trigonometric functions. This exploration is suitable for students and enthusiasts with a foundation in calculus and trigonometry.
Understanding the Components
The expression x³cos(x/2) + 1/2 is a composite function, a blend of a cubic polynomial (x³) and a trigonometric function (cos(x/2)). Let's examine each component separately:
-
x³: This is a simple cubic polynomial function. Its graph is a characteristic S-shaped curve, passing through the origin (0,0). It increases monotonically for positive x and decreases monotonically for negative x. Its derivative is 3x², and its second derivative is 6x. This indicates an inflection point at x=0, where the concavity changes.
-
cos(x/2): This is a cosine function with a horizontal compression by a factor of 2. The period of this function is 4π, double the period of the standard cosine function cos(x). The amplitude remains 1. Its range remains between -1 and 1. Its derivative is -1/2sin(x/2), and its second derivative is -1/4cos(x/2).
-
The Combination: Combining x³ and cos(x/2) through multiplication introduces complexity. The cubic polynomial's influence dominates at larger values of x, while the cosine function's oscillations introduce periodic variations. The constant term, +1/2, shifts the entire graph vertically upwards by 1/2 unit. This constant offset is crucial in understanding the function's overall behavior and potential intercepts.
Graphical Analysis
Visualizing the function is crucial for understanding its behavior. Plotting x³cos(x/2) + 1/2 using graphing software reveals a complex curve that exhibits both polynomial and trigonometric characteristics.
-
Oscillations: The cosine function introduces periodic oscillations, causing the graph to wave above and below the curve of x³. The amplitude of these oscillations increases as |x| increases, due to the influence of the x³ term.
-
Asymptotic Behavior: As x tends towards positive or negative infinity, the cubic term dominates, and the graph's behavior resembles that of a cubic polynomial. The oscillations become less pronounced relative to the overall growth or decline of the function.
-
Roots (Zeros): Finding the exact roots of the equation x³cos(x/2) + 1/2 = 0 is analytically challenging. Numerical methods, such as the Newton-Raphson method, are necessary to approximate the roots. The number of roots is infinite due to the oscillatory nature of the cosine function.
-
Extrema: The function possesses numerous local maxima and minima. These extrema are the points where the derivative of the function equals zero. Finding these points requires solving a complex equation involving both trigonometric and polynomial terms.
Derivatives and Integrals
Analyzing the derivatives and integrals of the function provides further insight into its properties:
-
First Derivative: Finding the first derivative requires applying the product rule of differentiation. This results in a complex expression involving both sine and cosine functions, along with polynomial terms. Solving for where the derivative is zero allows us to find critical points, which indicate potential local maxima and minima.
-
Second Derivative: The second derivative, similarly obtained through the product and chain rules, is even more complex. Its analysis provides information about the concavity of the function and the location of inflection points.
-
Indefinite Integral: The indefinite integral of x³cos(x/2) + 1/2 is challenging to express in a closed-form solution. It likely involves a combination of trigonometric functions and polynomial terms, potentially requiring integration by parts or other advanced techniques. Numerical integration methods would be necessary for practical applications.
Applications and Relevance
While the immediate application of this specific function might not be readily apparent in common engineering or physics problems, it serves as a valuable illustrative example within several mathematical contexts:
-
Numerical Analysis: This function serves as an excellent test case for numerical methods, particularly for finding roots, extrema, and evaluating definite integrals. Its complex nature necessitates the use of iterative and approximation techniques.
-
Approximation Theory: Understanding its behavior allows for the exploration of various approximation techniques, such as Taylor series expansions or Fourier series, for simplifying or approximating the function within specific intervals.
-
Mathematical Modeling: While not directly applicable to many standard physical phenomena, it could represent aspects of complex systems exhibiting both periodic and growth-related behaviors. Customized modifications of the function could potentially model specific scenarios.
-
Educational Tool: This function's complexity makes it an excellent tool for teaching advanced calculus concepts, emphasizing the application of differentiation, integration, and numerical methods. It demonstrates the challenges and rewards of analyzing composite functions.
Frequently Asked Questions (FAQ)
Q: Is there a closed-form solution for the indefinite integral of x³cos(x/2) + 1/2?
A: It's highly unlikely. The combination of a polynomial and a trigonometric function makes finding a closed-form antiderivative extremely difficult, if not impossible. Numerical integration techniques are typically employed for practical evaluation.
Q: How many roots does the function have?
A: The function has infinitely many roots. The oscillatory nature of the cosine function ensures that the graph intersects the x-axis (where y=0) at numerous points.
Q: How can I find the extrema of the function?
A: Find the first derivative, set it equal to zero, and solve for x. This will give you the x-coordinates of potential maxima and minima. You would then need to use the second derivative test to classify them (local maxima, local minima, or saddle points). Solving this equation analytically is very difficult; numerical methods are usually required.
Q: What software is best for visualizing this function?
A: Several software packages can effectively plot this function, including Mathematica, MATLAB, Maple, and various online graphing calculators (such as Desmos). These tools provide the capabilities for plotting, analyzing derivatives, and finding roots.
Q: What is the significance of the constant term +1/2?
A: The constant term vertically shifts the entire graph upwards by 1/2 unit. This alters the y-intercept and influences the location of roots and extrema. Without it, the graph would pass through the origin (0,0).
Conclusion
The mathematical expression x³cos(x/2) + 1/2, though seemingly simple at first glance, reveals a surprising richness and complexity upon closer inspection. Its blend of polynomial and trigonometric elements leads to a fascinating interplay of growth and oscillation. While its direct applications might not be immediately obvious in standard scientific domains, it serves as a valuable tool for exploring and reinforcing advanced calculus concepts, numerical methods, and the general understanding of function behavior. Its analysis provides a powerful example of the intricacies that can arise from combining seemingly simple functions and the need for sophisticated techniques to fully understand their properties. Further exploration of this function and similar composite functions can lead to a deeper appreciation of the elegance and challenges inherent in mathematical analysis.
Latest Posts
Latest Posts
-
How Much Is 1 Ampere
Sep 14, 2025
-
Soap Test For Water Hardness
Sep 14, 2025
-
Concrete Mix 1 2 3
Sep 14, 2025
-
Boiling Point Of Fahrenheit Scale
Sep 14, 2025
-
Three To One Amino Acid
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X3 Cos X/2 + 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.