Integrate Sin 3x Cos 2x
thesills
Sep 17, 2025 · 5 min read
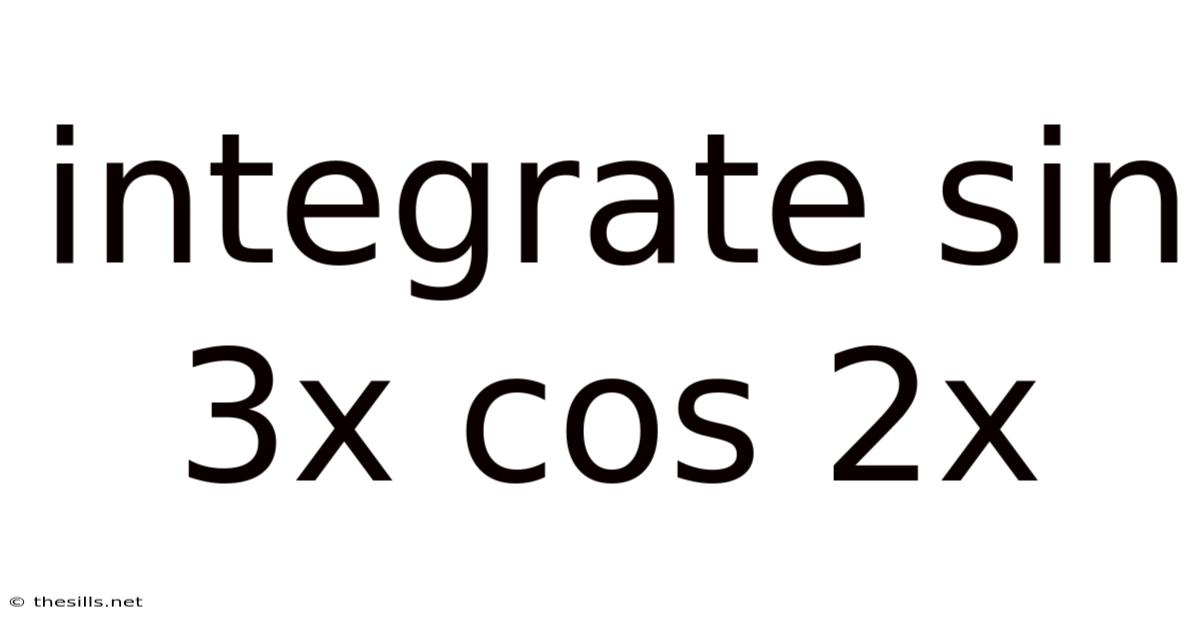
Table of Contents
Integrating sin 3x cos 2x: A Comprehensive Guide
Integrating trigonometric functions can often feel daunting, but with a systematic approach and understanding of key trigonometric identities, even complex integrals like ∫sin 3x cos 2x dx become manageable. This article will guide you through the process, explaining the steps, underlying principles, and providing additional insights to enhance your understanding of trigonometric integration. We will cover various methods and explore the nuances of each, ensuring a comprehensive grasp of this important calculus concept.
Introduction
The integral ∫sin 3x cos 2x dx presents a classic example of integrating a product of trigonometric functions. Direct integration isn't feasible; instead, we need to employ trigonometric identities to simplify the integrand before proceeding. The key here is to utilize product-to-sum identities, which transform products of trigonometric functions into sums or differences. This simplification allows us to integrate each term individually, leading to a straightforward solution.
Method 1: Using the Product-to-Sum Identity
The core of this method lies in the following product-to-sum identity:
sin A cos B = ½ [sin(A + B) + sin(A - B)]
Applying this identity to our integral, where A = 3x and B = 2x, we get:
sin 3x cos 2x = ½ [sin(3x + 2x) + sin(3x - 2x)] = ½ [sin 5x + sin x]
Now, our integral becomes significantly simpler:
∫sin 3x cos 2x dx = ½ ∫(sin 5x + sin x) dx
This integral can now be solved term by term using basic integration rules:
∫sin kx dx = (-1/k)cos kx + C, where k is a constant.
Therefore:
½ ∫(sin 5x + sin x) dx = ½ [(-1/5)cos 5x + (-1)cos x] + C = (-1/10)cos 5x - (1/2)cos x + C
Where C represents the constant of integration. This is our final solution using the product-to-sum identity.
Method 2: Using Complex Exponentials (Euler's Formula)
A more advanced, yet elegant method utilizes Euler's formula, which relates trigonometric functions to complex exponentials:
e^(ix) = cos x + i sin x
From this, we can derive expressions for sin x and cos x:
sin x = (e^(ix) - e^(-ix)) / (2i) cos x = (e^(ix) + e^(-ix)) / 2
Applying these to sin 3x and cos 2x:
sin 3x = (e^(3ix) - e^(-3ix)) / (2i) cos 2x = (e^(2ix) + e^(-2ix)) / 2
Substituting these into the integral:
∫sin 3x cos 2x dx = ∫[(e^(3ix) - e^(-3ix)) / (2i)] * [(e^(2ix) + e^(-2ix)) / 2] dx
This simplifies to:
(1/4i) ∫[e^(5ix) + e^(ix) - e^(-ix) - e^(-5ix)] dx
Now, integrating each term:
(1/4i) [ (1/5i)e^(5ix) + (1/i)e^(ix) - (-1/i)e^(-ix) - (-1/5i)e^(-5ix) ] + C
This expression may seem daunting, but observe that many terms cancel out and we can use Euler's formula in reverse to simplify back into trigonometric form. After simplification and collecting terms we arrive at the same result as before:
(-1/10)cos 5x - (1/2)cos x + C
Detailed Explanation of the Steps (Method 1)
Let's break down Method 1 step-by-step for a clearer understanding:
-
Identify the applicable trigonometric identity: The crucial step is recognizing that the integral involves a product of sine and cosine functions with different arguments. This immediately suggests the use of the product-to-sum identity.
-
Apply the product-to-sum identity: Substituting A = 3x and B = 2x into the identity sin A cos B = ½ [sin(A + B) + sin(A - B)] transforms the integrand into a sum of simpler sine functions.
-
Rewrite the integral: The original integral is now rewritten as a sum of two simpler integrals, each involving a single sine function.
-
Integrate each term separately: Each integral is solved using the standard integration rule for sine functions. Remember to include the constant of integration (C) at the end of the integration process.
-
Combine the results: The results from integrating each term are combined to obtain the final answer.
Addressing Potential Confusion
-
Constant of Integration: Remember to always add the constant of integration (C) after performing the indefinite integration. This accounts for the family of functions that share the same derivative.
-
Choosing the Right Method: Both methods (product-to-sum and Euler's formula) yield the same result. The product-to-sum method is generally simpler and more directly applicable for introductory calculus courses. The complex exponential method is a powerful tool with wider applications in advanced mathematics and physics.
-
Double-Checking Your Work: It's always beneficial to differentiate your final answer to verify that it indeed gives you the original integrand. This helps catch any potential errors during the integration process.
Frequently Asked Questions (FAQ)
-
Q: Can I use other trigonometric identities to solve this integral?
- A: While other identities might seem applicable, the product-to-sum identity is the most efficient and straightforward approach for this particular problem. Other identities might lead to more complex calculations.
-
Q: What if the arguments of sine and cosine were different multiples of x (e.g., sin 4x cos 7x)?
- A: The same product-to-sum identity applies. Simply substitute the appropriate values for A and B and follow the same procedure.
-
Q: Is there a general formula for integrating sin(ax)cos(bx)?
-
A: Yes, using the product-to-sum identity, the general solution to ∫sin(ax)cos(bx)dx is:
(-1/(2(a+b)))cos((a+b)x) + (-1/(2(a-b)))cos((a-b)x) + C
Note that this formula is not valid if a = b. In that case, the integral simplifies considerably.
-
Conclusion
Integrating sin 3x cos 2x, initially appearing complex, simplifies significantly using the appropriate trigonometric identity. Both the product-to-sum identity and the method using complex exponentials provide valid and equivalent solutions. Understanding these methods and their underlying principles is essential for mastering trigonometric integration. Remember to practice regularly, focusing on the application of trigonometric identities and the careful execution of integration rules to build your proficiency in calculus. Always check your work by differentiating the result to ensure accuracy. This thorough approach will equip you to tackle more complex trigonometric integrals with confidence and precision.
Latest Posts
Latest Posts
-
Equation For Combustion Of Ethane
Sep 17, 2025
-
Does Iron Float In Water
Sep 17, 2025
-
What Is Motion Of Particles
Sep 17, 2025
-
0 10 7 2 X 10 4
Sep 17, 2025
-
Highest 2 Digit Prime Number
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Integrate Sin 3x Cos 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.