0.10 / 7.2 X 10-4
thesills
Sep 17, 2025 · 5 min read
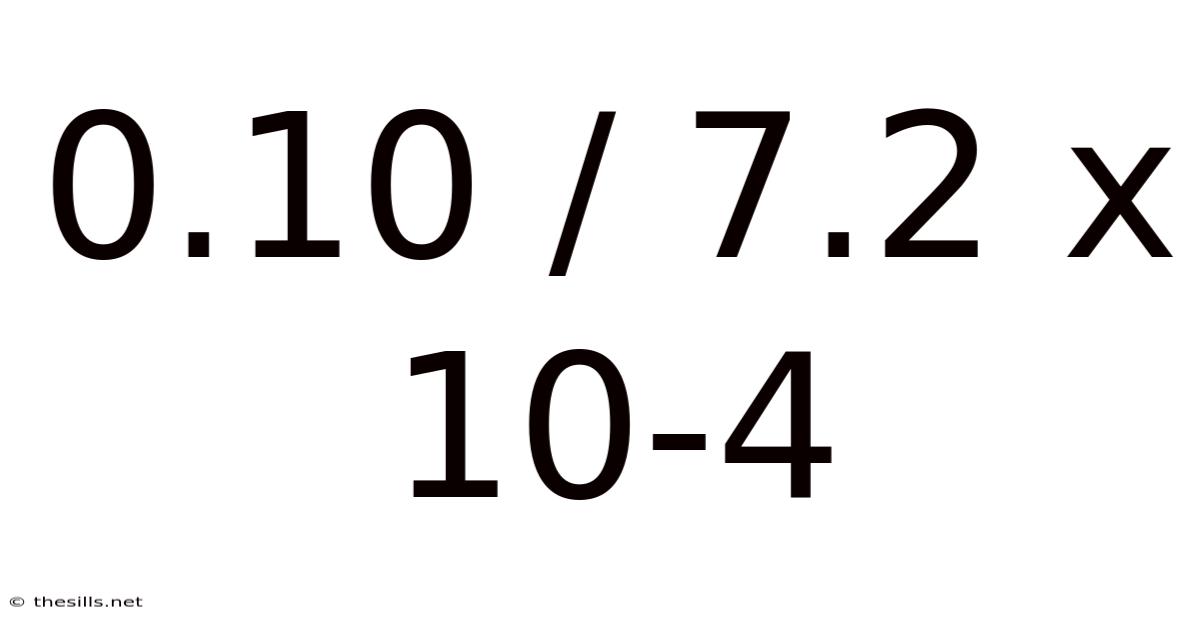
Table of Contents
Decoding 0.10 / 7.2 x 10⁻⁴: A Deep Dive into Scientific Notation and Calculation
This article will unravel the seemingly simple calculation of 0.10 / 7.2 x 10⁻⁴, explaining not only the solution but also the underlying principles of scientific notation, significant figures, and order of operations. Understanding this seemingly straightforward problem opens doors to a deeper comprehension of fundamental mathematical concepts crucial in various scientific fields. We'll break down the process step-by-step, addressing potential points of confusion and highlighting the importance of accuracy and precision in scientific calculations.
Understanding Scientific Notation
Before tackling the calculation, let's solidify our understanding of scientific notation. Scientific notation is a standardized way of writing very large or very small numbers. It expresses a number as a product of a coefficient (a number between 1 and 10) and a power of 10. For example:
- 1,000,000 can be written as 1 x 10⁶ (1 times 10 to the power of 6)
- 0.000001 can be written as 1 x 10⁻⁶ (1 times 10 to the power of -6)
The exponent (the small number written above and to the right of the 10) indicates how many places the decimal point needs to be moved to obtain the original number. A positive exponent means moving the decimal point to the right (larger number), while a negative exponent means moving it to the left (smaller number).
Analyzing the Components: 0.10 / 7.2 x 10⁻⁴
Let's examine each component of our calculation: 0.10, 7.2, and 10⁻⁴.
-
0.10: This is our dividend – the number being divided. Note the inclusion of the zero after the decimal point. This is significant and indicates that we have two significant figures. Significant figures represent the level of precision in a measurement.
-
7.2: This is our divisor – the number we are dividing by. It also has two significant figures.
-
10⁻⁴: This is a power of ten, representing a very small number (0.0001). It's crucial to understand this part as it impacts the magnitude of the final answer.
Step-by-Step Calculation: Applying the Order of Operations
The order of operations (PEMDAS/BODMAS) dictates the sequence in which we perform calculations: Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). In our case, we have division and multiplication. Since they have equal precedence, we perform them from left to right.
Step 1: Division
First, we divide 0.10 by 7.2:
0.10 / 7.2 ≈ 0.013888...
Step 2: Multiplication
Next, we multiply the result from Step 1 by 10⁻⁴:
0.013888... x 10⁻⁴ ≈ 0.0000013888...
Step 3: Scientific Notation
Finally, we convert the result to scientific notation:
0.0000013888... ≈ 1.39 x 10⁻⁶
We round the coefficient to two significant figures (matching the least number of significant figures in the original problem), resulting in 1.39. The exponent reflects the number of places the decimal point needed to be moved to obtain a coefficient between 1 and 10.
Scientific Notation and Significant Figures: A Deeper Look
The concept of significant figures is inherently linked to scientific notation. Significant figures represent the digits in a number that carry meaning contributing to its precision. Rules for determining significant figures include:
- All non-zero digits are significant.
- Zeros between non-zero digits are significant.
- Leading zeros (zeros to the left of the first non-zero digit) are not significant.
- Trailing zeros in a number containing a decimal point are significant.
- Trailing zeros in a number without a decimal point are ambiguous and should be avoided by using scientific notation.
In our example, both 0.10 and 7.2 have two significant figures. Therefore, our final answer should also have two significant figures to reflect the precision of the input values. Rounding to two significant figures is crucial to maintain the accuracy of our calculation and avoids overstating the precision of our result.
Addressing Potential Errors and Misconceptions
A common mistake is performing the multiplication before the division, ignoring the order of operations. This would lead to an incorrect answer.
Another potential issue is misinterpreting scientific notation or incorrectly rounding significant figures. Carefully following the rules of significant figures is critical for accurate scientific reporting.
Practical Applications and Relevance
Calculations involving scientific notation are ubiquitous in numerous scientific fields, including:
- Chemistry: Dealing with molar masses, concentrations, and reaction rates.
- Physics: Working with astronomical distances, atomic sizes, and physical constants.
- Engineering: Calculating forces, pressures, and energy values.
- Biology: Analyzing population sizes, cell dimensions, and genetic probabilities.
Mastering scientific notation and associated calculations is essential for anyone pursuing a career in STEM (Science, Technology, Engineering, and Mathematics) fields.
Frequently Asked Questions (FAQ)
Q1: Why is scientific notation important?
A1: Scientific notation provides a concise and efficient way to represent very large or very small numbers. It simplifies calculations and improves readability, preventing errors caused by cumbersome long numbers.
Q2: How do I determine the number of significant figures?
A2: Follow the rules outlined above. Remember to consider leading, trailing, and embedded zeros when counting significant figures. When multiplying or dividing, the result should have the same number of significant figures as the least precise measurement used in the calculation.
Q3: What if I have parentheses in the equation?
A3: If parentheses were present, you would perform the operations within the parentheses first, following the order of operations (PEMDAS/BODMAS).
Q4: Can I use a calculator for this type of calculation?
A4: Yes, scientific calculators are designed to handle scientific notation easily. However, it's crucial to understand the underlying principles to ensure you can perform the calculation manually and interpret the results correctly. Always check your calculator's settings for correct handling of scientific notation.
Conclusion: Mastering the Fundamentals
This in-depth analysis of the calculation 0.10 / 7.2 x 10⁻⁴ highlights the importance of understanding not just the mechanics of calculation but also the fundamental concepts underpinning scientific notation and significant figures. By mastering these principles, you'll build a stronger foundation in mathematics and science, empowering you to tackle more complex calculations with confidence and accuracy. Remember, precision and attention to detail are paramount in scientific work. The seemingly small details, like significant figures and the order of operations, significantly impact the accuracy and reliability of your results.
Latest Posts
Latest Posts
-
Integration Of Sin Square X
Sep 17, 2025
-
Weight Is Scalar Or Vector
Sep 17, 2025
-
Explain Overloading Of Household Circuit
Sep 17, 2025
-
Trace Of Product Of Matrices
Sep 17, 2025
-
South America Map Latitude Longitude
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 0.10 / 7.2 X 10-4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.