Integrate 1 1 Sin X
thesills
Sep 17, 2025 · 5 min read
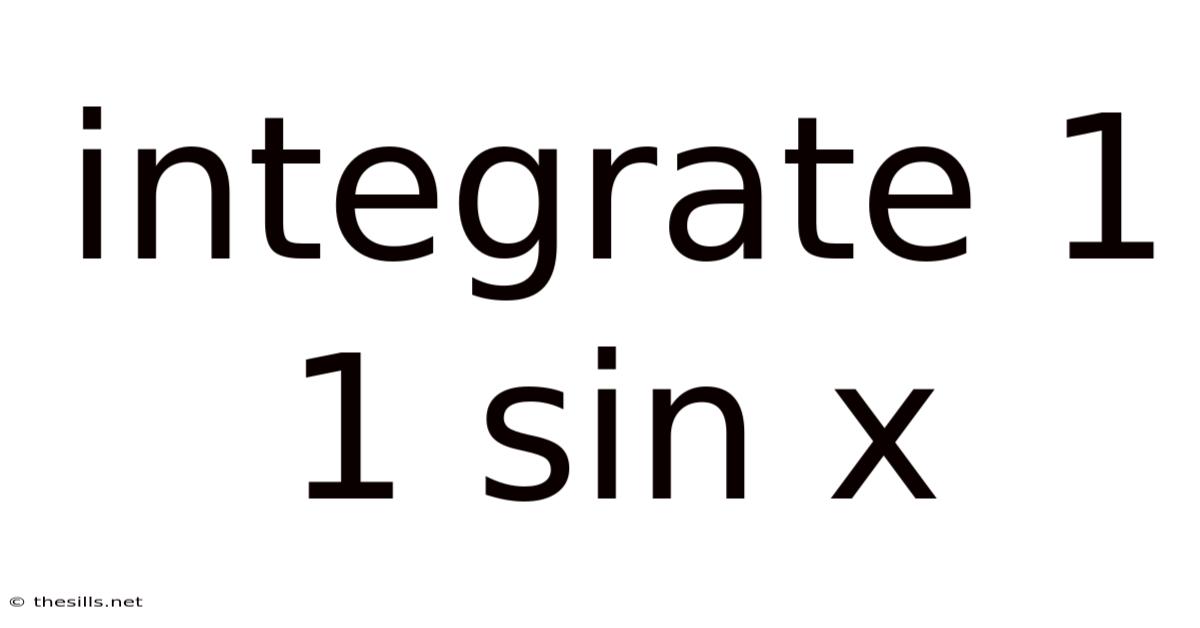
Table of Contents
Integrating 1 + sin x: A Comprehensive Guide
Integrating 1 + sin x might seem like a straightforward calculus problem, but understanding the nuances of its solution provides a valuable insight into fundamental integration techniques. This comprehensive guide will walk you through the process, explaining the underlying principles and offering practical applications. We'll cover the basic steps, delve into the underlying theory, address frequently asked questions, and provide examples to solidify your understanding. This will equip you with the skills to tackle more complex integration problems involving trigonometric functions.
Introduction: Understanding the Problem
The integral ∫(1 + sin x) dx represents the task of finding a function whose derivative is 1 + sin x. This seemingly simple problem serves as an excellent introduction to several key concepts in integral calculus, including the linearity of integration and the integration of trigonometric functions. The solution involves applying basic integration rules and understanding the antiderivative of both constant and trigonometric functions. This seemingly simple problem forms a foundation for understanding more complex trigonometric integrations later on.
Step-by-Step Integration of 1 + sin x
The process of integrating 1 + sin x relies on the linearity of integration, which states that the integral of a sum is the sum of the integrals. This allows us to break down the problem into two simpler integrals:
-
Integrate the constant term: The integral of 1 with respect to x is simply x. This is because the derivative of x is 1. Therefore, ∫1 dx = x + C₁ (where C₁ is the constant of integration).
-
Integrate the sine term: The integral of sin x with respect to x is -cos x. This is a standard integral derived from the fact that the derivative of -cos x is sin x. Therefore, ∫sin x dx = -cos x + C₂ (where C₂ is another constant of integration).
-
Combine the results: Since integration is linear, we can sum the results of steps 1 and 2:
∫(1 + sin x) dx = ∫1 dx + ∫sin x dx = x + C₁ + (-cos x + C₂) = x - cos x + C
Where C = C₁ + C₂ is the overall constant of integration. Combining the constants of integration is a standard practice.
Therefore, the indefinite integral of 1 + sin x is x - cos x + C, where C represents the constant of integration. Remember, the constant of integration is crucial because the derivative of any constant is zero. This means infinitely many functions can have the same derivative.
A Deeper Dive: The Theoretical Underpinnings
The solution above relies on several fundamental concepts from calculus:
-
The Fundamental Theorem of Calculus: This theorem establishes a connection between differentiation and integration. It states that integration is the reverse process of differentiation. This is precisely what we are applying when we find the antiderivative of 1 + sin x.
-
Linearity of Integration: As mentioned earlier, the linearity of integration is a powerful property that allows us to break down complex integrals into simpler ones. It states that:
∫[af(x) + bg(x)] dx = a∫f(x) dx + b∫g(x) dx, where 'a' and 'b' are constants.
-
Antiderivatives: An antiderivative of a function f(x) is a function F(x) whose derivative is f(x), i.e., F'(x) = f(x). The indefinite integral ∫f(x) dx represents the family of all antiderivatives of f(x), differing only by a constant. In our case, x - cos x is an antiderivative of 1 + sin x.
-
Trigonometric Identities: While not directly used in this simple integration, understanding trigonometric identities is crucial for handling more complex integrals involving trigonometric functions. These identities allow us to manipulate the integrand into a form that's easier to integrate.
Practical Applications and Examples
The integral ∫(1 + sin x) dx has applications in various fields, including:
-
Physics: This integral can appear in problems involving motion under the influence of gravity and simple harmonic motion. For instance, if 1 + sin x represents acceleration, integrating it once gives velocity, and integrating again gives displacement.
-
Engineering: Integrals of this form are encountered in problems involving oscillations and wave phenomena.
-
Economics: While less direct, similar integrals appear in models involving periodic changes or growth patterns.
Example 1: Definite Integral
Let's calculate the definite integral of 1 + sin x from 0 to π:
∫₀^π (1 + sin x) dx = [x - cos x]₀^π = (π - cos π) - (0 - cos 0) = π - (-1) - (0 - 1) = π + 2
Example 2: A slightly more complex problem:
Consider the integral ∫(2 + 3sin x) dx. Using the linearity of integration:
∫(2 + 3sin x) dx = ∫2 dx + ∫3sin x dx = 2x + 3(-cos x) + C = 2x - 3cos x + C
Frequently Asked Questions (FAQ)
Q1: Why is the constant of integration (C) important?
A1: The constant of integration is crucial because the derivative of a constant is always zero. This means that infinitely many functions can have the same derivative. The constant of integration accounts for this ambiguity. For indefinite integrals, it's essential to include the constant C. For definite integrals, the constant cancels out during the evaluation.
Q2: What if the integral was ∫(1 - sin x) dx?
A2: The process is very similar. The integral of -sin x is cos x. Therefore, ∫(1 - sin x) dx = x + cos x + C
Q3: How can I handle more complex trigonometric integrals?
A3: For more complex integrals involving trigonometric functions, you might need to use techniques like:
- Trigonometric substitution: Substituting trigonometric functions for variables to simplify the integrand.
- Integration by parts: A technique used to integrate products of functions.
- Trigonometric identities: Using identities to rewrite the integrand in a more manageable form.
Q4: Can I use a calculator or software to solve this integral?
A4: While calculators and software like Mathematica or Maple can perform symbolic integration, understanding the manual process is crucial for developing a strong foundation in calculus. Using these tools should come after you understand the underlying principles.
Conclusion: Mastering the Fundamentals
Integrating 1 + sin x, while seemingly simple, provides a robust foundation for understanding fundamental integration techniques. By mastering this basic integral, you build a strong base for tackling more challenging integration problems involving trigonometric functions and other complex functions. Remember the key concepts: linearity of integration, the constant of integration, and the antiderivatives of basic functions. Practice is key to solidifying your understanding, so work through various examples and gradually increase the complexity of the problems you tackle. The ability to integrate functions accurately and efficiently is a cornerstone of success in calculus and many related fields. So keep practicing, and you'll find yourself confident in tackling even the most challenging integrals.
Latest Posts
Latest Posts
-
Burning Of Ammonia In Oxygen
Sep 17, 2025
-
Equation Of Hcl And Naoh
Sep 17, 2025
-
Integration Of 1 Cosx Sinx
Sep 17, 2025
-
7 X 2 X 7
Sep 17, 2025
-
Newman Projection Of N Butane
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Integrate 1 1 Sin X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.